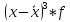Задание № 2

Используя показатели структуры реализации продукции предприятий в разрезе отдельных филиалов в 2011 и 2012 гг., рассчитанные в задаче 1, дайте характеристику изменения удельного веса каждого филиала в общем объеме реализации. С помощью обобщающих показателей структурных сдвигов определите, как в целом изменилась структура реализации за год. Расчеты выполните в табличной форме. Напишите, в чем состоит смысл рассчитанных показателей

Решение

Произведем расчеты в таблице:

Филиал
№ 1	16,0	25,4	9,4	88,8	0,59
№ 2	10,3	11,2	0,9	0,8	0,08
№ 3	38,8	30,7	8,1	65,9	0,21
№ 4	34,8	32,7	2,2	4,8	0,06
В целом по предприятию	100,0	100,0	20,6	160,3	0,94

Сумма абсолютных долей:

Показатель степени интенсивности абсолютного структурного сдвига:

Квадратическое изменение долей:

Среднее линейное измерение по модулю:

Задание № 3

Имеются данные, характеризующие выбросы загрязняющих веществ в 2012 году по районам города:

Район	Выбросы загрязняющих веществ, тысяч тонн	Выбросы загрязняющих веществ в расчёте на одного жителя, кг	Темп роста общего объёма выбросов в 2012 г. по сравнению с 2011 г., %	Доля выбросов без очистки в общем объёме выбросов, %
1	3,3	7,2	110	90
2	9	28,2	118	82
3	1,2	3,7	133	95
4	4,2	9,6	168	96

Рассчитайте показатели в среднем по городу. Укажите, какие виды и формы средних вы использовали.

Решение

Среднее количество выбросов на район (средняя арифметическая простая):

Среднее количество выбросов на одного жителя (средняя гармоническая):

Темпы роста количества выбросов (средняя гармоническая):

Доля выбросов без очистки в общем объеме (средняя арифметическая взвешенная):

Задание № 4

На основе данных в таблице определите:

1. Характеристики центра распределения: среднее значение признака, модальное значение признака, медианное значение признака.

2. Показатели размера и интенсивности вариации: среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации.

3. Показатели формы распределения: коэффициенты асимметрии и эксцесса.

4. Постройте гистограмму распределения.

5. Раскройте содержание всех рассчитанных показателей и их пред- ставление на графике.

В лаборатории комбикормового завода произведена контрольная проверка партии пшеницы, поступившей для производства комбикормов, на содержание протеина. В результате получены следующие данные:

Содержание протеина, %	Число проб
6	2
7	5
8	6
9	10
10	19
11	6
12	2
Итого	50

Решение

Сведем расчеты в таблицу:

					Накопленная частота, S
6		2		12	2		6,6	21,78				-71,87	237,18
7		5		35	7		11,5	26,45				-60,84	139,92
8		6		48	13		7,8	10,14				-13,18	17,14
9		10		90	23		3	0,9				-0,27	0,08
10		19		190	42		13,3	9,31				6,52	4,56
11		6		66	48		10,2	17,34				29,48	50,11
12		2		24	50		5,4	14,58				39,37	106,29
		50		465			57,8	100,5				-70,80	555,29

1. Средняя арифметическая взвешенная:

2. Мода:

Максимальное значение повторений при , следовательно мода равняется 10.

3. Медиана:

Медиана – значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Находим , при котором накопленная частота будет больше, это значение, следовательно медиана равняется 10.

4. Среднее линейное отклонение:

5. Дисперсия:

6. Среднее квадратическое отклонение:

7. Коэффициент вариации:

Поскольку , то совокупность однородна, а вариация слабая, соответственно полученным результатам можно доверять.

8. Коэффициент асимметрии:

9. Коэффициент эксцесса:

10. Полигон:

Вывод: среднее значение составляет 9,3. Наиболее часто встречающееся значение равно 10, при этом 50% наблюдений меньше значения 10, а остальные больше значения 10. Поскольку 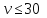, то совокупность однородна, а вариация слабая, соответственно полученным результатам можно доверять. Отрицательный знак свидетельствует о наличии левосторонней асимметрии. Так как эксцесс отрицателен, то распределение плосковершинное.