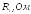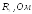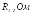- •1) Записать уравнения по законам Кирхгофа в дифференциальной и комплексной формах.
- •2) Определить комплексные действующие значения токов во всех ветвях методом контурных токов и методом узловых потенциалов. Свести результаты расчетов в одну таблицу.
- •4) Проверить баланс комплексных мощностей в цепи.
Некоммерческое акционерное общество
«АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ»
Кафедра теоретических основ электротехники

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №2
По дисциплине «Основы теории цепей»
На тему «Расчёт разветвлённых линейных электрических цепей однофазного синусоидального тока»
Специальность «Информационные системы»
Выполнил Ануарбеков Шыңғыс Группа ИС-16-2
Принял доцент каф. ТОЭ Айтжанов Н.М.
_________ «____»____________2017г.
Алматы 2017
Содержание
Введение...................................................................................................................3
Задание.....................................................................................................................4
Расчетная часть........................................................................................................6
Уравнения по законам Кирхгофа в двух формах.........................................6
Методы контурных токов и узловых потенциалов......................................8
Свод результатов расчетов в таблицу.........................................................13
Метод эквивалентного генератора..............................................................13
Баланс комплексных мощностей................................................................17
Мгновенные значения токов и график тока................................................17
Заключение.............................................................................................................19
Список литературы................................................................................................20
Введение
Цель работы: умение составлять систему уравнения по законам Кирхгофа для разветвлённых электрических цепей однофазного синусоидального тока, рассчитывать токи методом контурных токов, методом узловых потенциалов в комплексной форме, методом эквивалентного генератора.
Дана
электрическая цепь, в которой действуют
источники синусоидальной ЭДС
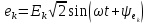 и синусоидального тока
и синусоидального тока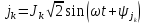 (см. рисунок 2.1-2.10). Действующие значения
ЭДС
(см. рисунок 2.1-2.10). Действующие значения
ЭДС и тока источника тока
и тока источника тока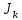 , а также начальные фазы
, а также начальные фазы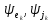 приведены в таблице 2.2. Параметры
электрической цепи приведены в таблицах
2.1, 2.3.
приведены в таблице 2.2. Параметры
электрической цепи приведены в таблицах
2.1, 2.3.
Таблица 2.1
|
Год поступления |
Первая буква фамилии | |||||||||
|
Четный |
А БВ |
ГДЕ |
ЖЗИ |
КЛ |
МН |
ОПР |
СТ У |
ФХЦ |
ЧШ Щ |
ЭЮ Я |
|
Нечетный |
КЛ |
ОПР |
СТ У |
ФХЦ |
АБ В |
ГД Е |
ЖЗИ |
МН |
ЭЮ Я |
ЧШЩ |
|
№ схемы |
3.1 |
3.2 |
3.3 |
3.4 |
3.5 |
3.6 |
3.7 |
3.8 |
3.9 |
3.10 |
|
|
3 |
10 |
20 |
10 |
40 |
10 |
40 |
20 |
10 |
40 |
|
|
5 |
2 |
30 |
20 |
16 |
20 |
10 |
60 |
20 |
5 |
|
|
8 |
6 |
25 |
5 |
20 |
40 |
30 |
10 |
50 |
12 |
|
|
2 |
16 |
65 |
25 |
15 |
100 |
50 |
40 |
40 |
18 |
|
|
4 |
25 |
20 |
10 |
8 |
10 |
10 |
10 |
30 |
30 |
|
|
10 |
10 |
15 |
30 |
15 |
25 |
40 |
5 |
60 |
40 |
|
|
6 |
5 |
20 |
8 |
5 |
20 |
20 |
18 |
40 |
10 |
|
|
18 |
10 |
30 |
20 |
8 |
50 |
30 |
10 |
20 |
30 |
Таблица 2.2
|
Год поступления |
Последняя цифра студенческого билета | |||||||||
|
Четный |
0 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
Нечетный |
2 |
5 |
6 |
1 |
3 |
4 |
7 |
8 |
9 |
0 |
|
|
10 |
20 |
15 |
30 |
25 |
16 |
12 |
30 |
40 |
18 |
|
|
20 |
12 |
18 |
28 |
30 |
35 |
40 |
15 |
8 |
25 |
|
|
30 |
15 |
20 |
10 |
16 |
15 |
45 |
50 |
30 |
20 |
|
|
35 |
20 |
15 |
25 |
10 |
18 |
32 |
40 |
42 |
35 |
|
|
10 |
15 |
8 |
5 |
20 |
10 |
6 |
12 |
3 |
4 |
|
|
30 |
40 |
25 |
45 |
-40 |
60 |
0 |
35 |
50 |
70 |
|
|
120 |
80 |
90 |
-30 |
-60 |
-40 |
30 |
-10 |
-20 |
-90 |
|
|
130 |
150 |
180 |
-45 |
-30 |
-60 |
-90 |
40 |
15 |
20 |
|
|
0 |
20 |
90 |
-60 |
-45 |
-50 |
45 |
70 |
30 |
120 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Таблица 2.3
|
Год поступления |
Предпоследняя цифра студенческого билета | |||||||||
|
Четный |
2 |
3 |
4 |
8 |
0 |
1 |
5 |
7 |
6 |
9 |
|
Нечетный |
8 |
2 |
0 |
7 |
6 |
4 |
3 |
5 |
9 |
1 |
|
|
60 |
100 |
40 |
50 |
80 |
20 |
15 |
25 |
30 |
12 |
|
|
50 |
45 |
90 |
40 |
30 |
25 |
10 |
20 |
18 |
6 |
|
|
6 |
10 |
8 |
15 |
20 |
30 |
25 |
40 |
60 |
10 |
|
|
120 |
100 |
80 |
60 |
40 |
20 |
10 |
8 |
15 |
45 |
|
МЭГ, График тока |
i4 |
i1 |
i2 |
i3 |
i4 |
i1 |
i2 |
i3 |
i4 |
i1 |
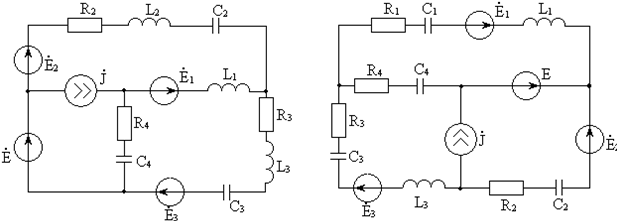
Рисунок 2.1
Задание:
1) Записать уравнения по законам Кирхгофа в дифференциальной и комплексной формах.
2) Определить комплексные действующие значения токов во всех ветвях методом контурных токов и методом узловых потенциалов. Свести результаты расчетов в одну таблицу.
3) Определить комплекс действующего значения требуемого тока (см. таблицу 2.3) методом эквивалентного генератора.
4) Проверить баланс комплексных мощностей в цепи.
5)
Записать мгновенные значения токов
всех ветвей и построить график одного
из токов i(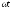 )
(см. таблицу 2.3).
)
(см. таблицу 2.3).
Расчетная часть
1) Записать уравнения по законам Кирхгофа в дифференциальной и комплексной формах.
Законы Кирхгофа в дифференциальной форме. Законы Кирхгофа в дифференциальной форме записываются для мгновенных значений переменных токов и напряжений.
Первый
закон Кирхгофа: алгебраическая сумма
мгновенных значений токов в узле схемы
равна нулю:
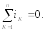 Со знаком «+» записываются токиік,
положительные направления которых
направлены к рассматриваемому узлу, со
знаком «-» записываются токи
ік,
положительные направления которых
направлены от данного узла (или наоборот).
Число
уравнений, составляемых по первому
закону Кирхгофа, равно
Со знаком «+» записываются токиік,
положительные направления которых
направлены к рассматриваемому узлу, со
знаком «-» записываются токи
ік,
положительные направления которых
направлены от данного узла (или наоборот).
Число
уравнений, составляемых по первому
закону Кирхгофа, равно
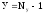 ,
где
,
где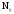 -
число узлов в цепи. В цепи (рис 1.1) имеются
4 узла, исходя из этого У = 4-1 = 3 (количество
уравнений поI
закону Кирхгофа). Следовательно,
достаточно записать уравнения для узлов
1, 2 и 3:
-
число узлов в цепи. В цепи (рис 1.1) имеются
4 узла, исходя из этого У = 4-1 = 3 (количество
уравнений поI
закону Кирхгофа). Следовательно,
достаточно записать уравнения для узлов
1, 2 и 3:
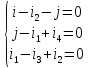
Второй закон Кирхгофа: алгебраическая сумма мгновенных ЭДС всех источников напряжения в любом замкнутом контуре схемы равна алгебраической сумме мгновенных напряжений на всех остальных элементах того же контура:
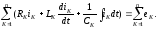
Второй
закон Кирхгофа записывается для
независимых контуров схемы, независимые
контура выбираются так же, как и для
цепей постоянного тока. Со знаком «+»
записываются мгновенные напряжения,
если положительные направления токов
ік
и направление обхода контура совпадают,
в противном случае напряжения записываются
со знаком «-». Мгновенные ЭДС
ек
записываются со знаком «+», если
положительные направления
ек
и направление обхода контура совпадают.
Число уравнений, составляемых по второму
закону Кирхгофа, равно:
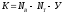 ,
где
,
где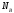 - число ветвей,
- число ветвей,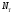 - число источников тока. Исходя из этого,
в цепи (рис 2.1) 6 ветвей, 1 источник тока
и как было выше сказано – 4 узла.
Следовательно, для второго закона
Кирхгофа понадобится К = 6-1-3=2 уравнения.
Выбираем два независимых контура, не
имеющих источника тока, затем произвольно
выбираем обход контура (рис 2.1). И для
каждого контура (внешний контур и контур
2342) запишем уравнение поII
закону Кирхгофа:
- число источников тока. Исходя из этого,
в цепи (рис 2.1) 6 ветвей, 1 источник тока
и как было выше сказано – 4 узла.
Следовательно, для второго закона
Кирхгофа понадобится К = 6-1-3=2 уравнения.
Выбираем два независимых контура, не
имеющих источника тока, затем произвольно
выбираем обход контура (рис 2.1). И для
каждого контура (внешний контур и контур
2342) запишем уравнение поII
закону Кирхгофа:
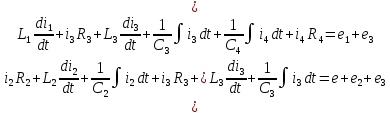
Общая система уравнений по законам Кирхгофа в дифференциальной форме будет выглядеть следующим образом:
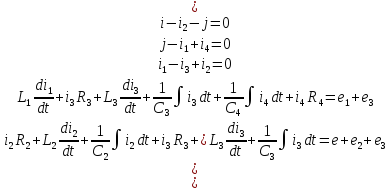
Законы Кирхгофа в комплексной форме.
Для узла электрической цепи переменного тока по первому закону Кирхгофа сумма мгновенных значений токов, направленных к узлу, равна сумме мгновенных значений токов, направленных от узла. То же самое правило справедливо и при записи токов в комплексной форме. Запишем уравнения для 1, 2, 3 узлов:
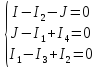
Для замкнутого контура электрической цепи переменного тока по второму закону Кирхгофа алгебраическая сумма мгновенных значений ЭДС, действующих в контуре, равна алгебраической сумме мгновенных значений падений напряжения на отдельных его участках. Приписав ЭДС и токам, совпадающим по направлению с направлением обхода контура, знак плюс, а несовпадающим – минус, получим при комплексной записи для любого замкнутого контура:
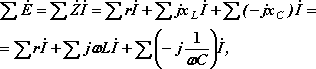
Таким образом, для всякого замкнутого контура алгебраическая сумма комплексных ЭДС источников питания равна алгебраической сумме комплексных падений напряжений. Выбираем два независимых контура, не имеющих источника тока, затем произвольно выбираем обход контура (рис 2.1). И для каждого контура (внешний контур и контур 2-3-4-2(узлы)) запишем уравнение по II закону Кирхгофа:
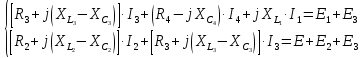
Общая система уравнений по законам Кирхгофа в комплексной форме будет выглядеть следующим образом:
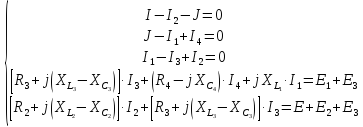

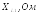
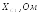
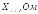
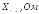
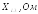
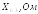
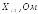
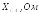
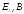
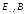
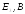

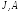
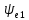 ,
град
,
град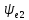 ,
град
,
град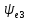 ,
град
,
град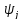 ,
град
,
град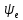 ,
град
,
град