
9
.docЛекция № 9
План:
1).Теорема об ускорении точек твердого тела при плоскопараллельном движении.
2).Мгновенный центр ускорений.
3).Основные способы вычисления углового ускорения при плоскопараллельном движении.
4).Сложное движение точки.
5).Теорема о сложении скоростей.
6).Теорема о сложении ускорений (т.Кориолиса). Модуль и направление поворотного ускорения.
-
Теорема об ускорении точек твердого тела при плоскопараллельном движении.
Теорема: Ускорение точки плоской фигуры равно сумме ускорения полюса и ускорения данной точки во вращательном движении вокруг полюса.
Доказательство:
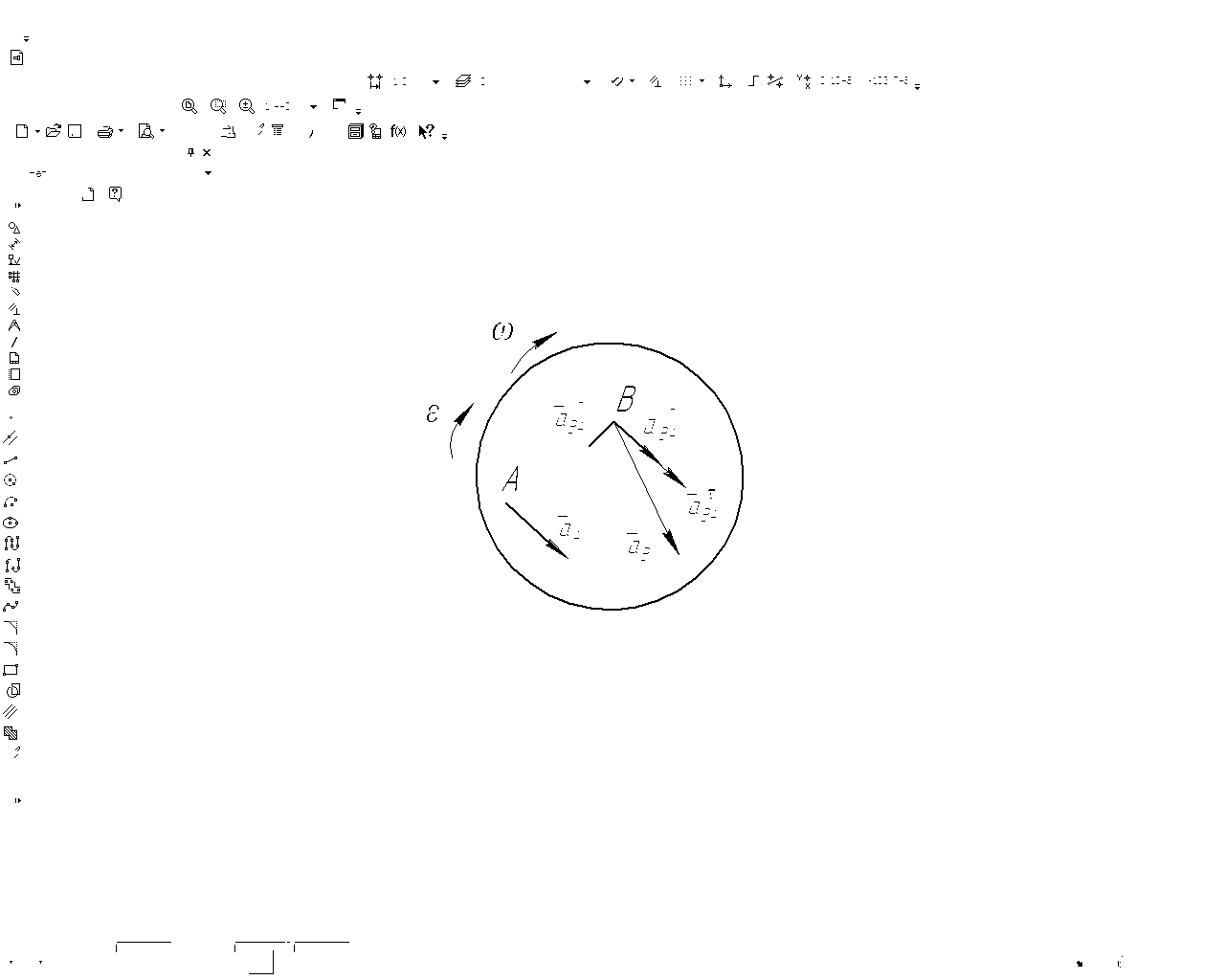
Дано:
![]() .
Ускорение точки В в её сложном движении:
.
Ускорение точки В в её сложном движении:
![]()
где относительное движение-вращение вокруг полюса А.
Переносное движение
– поступательное вместе с полюсом,
![]()
![]()
2) Мгновенный центр ускорений.
Мгновенным центром ускорений (МЦУ) называется точка Q плоской фигуры, ускорение которой в данный момент времени равно нулю: aQ=0. Если выбрать в качестве полюса МЦУ , то теорема о сложении ускорений дает
![]()
Ускорение точек плоской фигуры- это их ускорения в относительном вращении фигуры вокруг мгновенного центра ускорений.
Согласно формуле, получим для модуля ускорения точки плоской фигуры соотношение:
![]()
-ускорения точек
плоской фигуры пропорциональны
расстояниям от этих точек до МЦУ, а
коэффициентом пропорциональности
является
![]() .
.
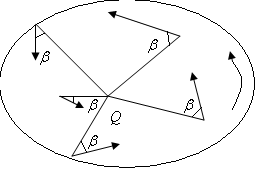
В каждый момент
времени имеет место распределение
ускорений точек плоской фигуры, показанное
на рисунке, где угол
![]() определяется по формуле:
определяется по формуле:
![]()
![]()
В частных случаях получаем:
1. Если
![]() ,
а
,
а
![]() ,
то угол
,
то угол
![]() ,
т.е ускорения всех точек направлены к
мгновенному центру ускорений. (рис.а)
,
т.е ускорения всех точек направлены к
мгновенному центру ускорений. (рис.а)
2. Если
![]() ,
а
,
а
![]() ,
то угол
,
то угол
![]() ,и
ускорения всех точек перпендикулярны
направлениям на МЦУ. (рис.б)
,и
ускорения всех точек перпендикулярны
направлениям на МЦУ. (рис.б)
3.Если
![]() и
и
![]() ,то
мгновенный центр ускорения находится
в бесконечности, а ускорения всех точек
векторно равны (мгновенно поступательное
движение). (рис.в)
,то
мгновенный центр ускорения находится
в бесконечности, а ускорения всех точек
векторно равны (мгновенно поступательное
движение). (рис.в)


-
Основные способы вычисления углового ускорения при плоскопараллельном движении.
Рассмотрим теперь различные случаи определения положения МЦУ.
1. Если известно
ускорение какой либо точки aM,
а также угловая скорость
![]() и угловое ускорение
и угловое ускорение
![]() плоской фигуры (рис.а), то для нахождения
МЦУ необходимо сделать следующее:
плоской фигуры (рис.а), то для нахождения
МЦУ необходимо сделать следующее:
а) вычислить угол
![]() ;
б) построить луч, повернув вектор aM
на угол
;
б) построить луч, повернув вектор aM
на угол
![]() по
направлению углового ускорения; в)
отложить на луче отрезок
по
направлению углового ускорения; в)
отложить на луче отрезок
![]() .
.


Легко убедиться,
что получившаяся точка Q
и есть МЦУ, поскольку
![]()
2. Если известны
ускорения двух точек
![]() и
и
![]() ,
и они не лежат на параллельных прямых
(рис.б), то для нахождения МЦУ необходимо
сделать следующее: а) построить вектор
,
и они не лежат на параллельных прямых
(рис.б), то для нахождения МЦУ необходимо
сделать следующее: а) построить вектор
![]() ,
он покажет направление углового
ускорения; б) определить угол
,
он покажет направление углового
ускорения; б) определить угол
![]() как угол между вектором
как угол между вектором
![]() и отрезком AB; в) построить лучи, повернув
векторы
и отрезком AB; в) построить лучи, повернув
векторы
![]() и
и
![]() на
угол
на
угол
![]() по направлению углового ускорения. На
пересечении лучей и находится МЦУ.
по направлению углового ускорения. На
пересечении лучей и находится МЦУ.
3. Если известны
ускорения двух точек
![]() и
и
![]() ,
и они лежат на параллельных прямых, то
может быть несколько случаев определения
положения МЦУ. МЦУ находится на пересечении
линий, проходящих через начала и концы
векторов ускорений.
,
и они лежат на параллельных прямых, то
может быть несколько случаев определения
положения МЦУ. МЦУ находится на пересечении
линий, проходящих через начала и концы
векторов ускорений.

4. Если известны
ускорения двух точек
![]() и
и
![]() ,
и они лежат на одной прямой (это может
быть при
,
и они лежат на одной прямой (это может
быть при
![]() =0
и, соответственно, при
=0
и, соответственно, при
![]() =0),
то возможные случаи определения положения
МЦУ представлены на рисунке. МЦУ находится
на пересечении данной линии с линией,
проходящей через концы векторов
ускорений, повернутых на угол 900.
=0),
то возможные случаи определения положения
МЦУ представлены на рисунке. МЦУ находится
на пересечении данной линии с линией,
проходящей через концы векторов
ускорений, повернутых на угол 900.
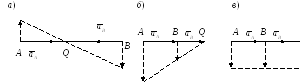
Отметим, что эти
случаи соответствуют мгновенному
поступательному движению. При этом
![]() и
и
![]() ,
МЦУ находится в бесконечности, а ускорения
всех точек векторно равны.
,
МЦУ находится в бесконечности, а ускорения
всех точек векторно равны.
Следует понимать, что МЦУ и МЦС – это различные точки плоской фигуры(они совпадают лишь при вращательном движении). Например, МЦС катящегося без скольжения колеса находится в точке касания с поверхностью. Если колесо катится равномерно по прямолинейному пути, то центр колеса движется равномерно и прямолинейно, т.е. МЦУ находится в центре колеса.
4) Сложное движение точки.
Сложным - называется такое движение точки (тела), которое рассматривается одновременно в разных системах отсчета.
Например: пассажир, перемещается в вагоне движущегося поезда, человек перемещающийся по лестнице движущегося эскалатора.
При описании сложного движения точки одну из систем отсчета считают неподвижной (её называют основной), другая же рассматривается как подвижная .

О,X/,Y/,Z/-основная система координат.
O,X,Y,Z- подвижная система координат.
(.) М- движущаяся точка.
В таком случае сразу можно рассматривать три движения: абсолютное, относительное, переносное.
А) Абсолютное
движение -
называется движение точки по отношению
к основной системе отсчета. Соответственно
скорость и ускорение точки по отношению
к основной система отсчета называется
абсолютным ускорением
![]()
![]()
Относительным
движением
- называется движение точки по отношению
к подвижной системе отсчета. Соответственно
скорость и ускорение точки по отношению
к подвижной системе отсчета называется
относительной скоростью
![]() и
относительным ускорением
и
относительным ускорением
![]() (r
от латинского relativus-
относительный). Положение точки М
относительно неподвижной системы
отсчета определяется радиус вектором
(r
от латинского relativus-
относительный). Положение точки М
относительно неподвижной системы
отсчета определяется радиус вектором![]() проведенным в точке М из О1.Изменение
радиус-вектора
проведенным в точке М из О1.Изменение
радиус-вектора
![]() характеризует движение точки:
характеризует движение точки:
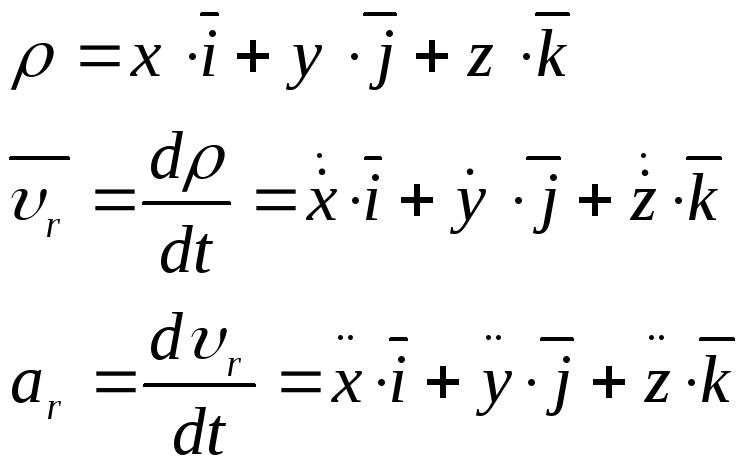
Б) Движение подвижной системы отсчета относительно неподвижной системы отсчета называется переносным движением. Движущаяся точка в разные моменты времени занимает различное положение в подвижной системе отсчета, т.е. совпадает с различными ее точками.
Переносной
скоростью
![]() и переносным ускорением
и переносным ускорением
![]() называют скорость и ускорение той точки
подвижной системы отсчета , с которой
в данный момент времени совпадает
движущаяся точка.
называют скорость и ускорение той точки
подвижной системы отсчета , с которой
в данный момент времени совпадает
движущаяся точка.
![]()
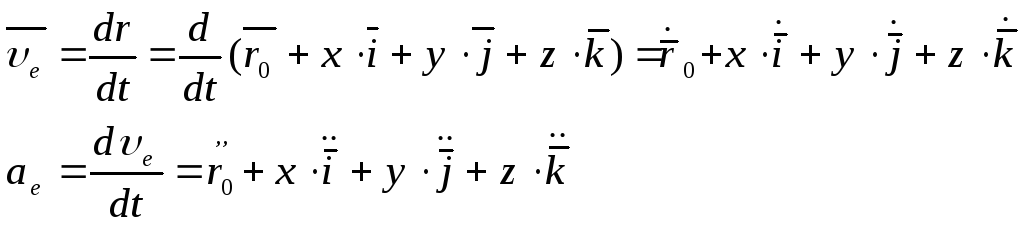
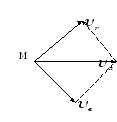
Пример: человек идет по вращающейся с некоторой угловой скоростьюW круглой горизонтальной платформе, двигаясь все время по определенному ее радиусу от центра платформы. Система отсчета связанная с Землей – неподвижная. Система отсчета связанная с платформой - подвижная.
![]()
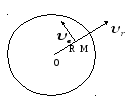
![]()
Тогда движение
человека относительно платформы является
относительным, движение человека
относительно Земли абсолютным, движение
платформы переносным.
![]() человека
направлена по радиусу.
человека
направлена по радиусу.
![]() перпендикулярно
радиусу платформы.
перпендикулярно
радиусу платформы.
5.Теорема о сложении скоростей.
При сложном движении точки абсолютная скорость точки равна векторной сумме относительной и переносной скорости.
![]()
Доказательство: Пусть o1, x1, y1, z1 – неподвижная система отсчета; o, x, y, z – подвижная система отсчета.x, y, z- координаты движущейся точки М в подвижной системе отсчета; r, r0-радиус-векторы точек М и О в неподвижной системе отсчета; ρ - радиус-вектор точки М в подвижной системе отсчета.
и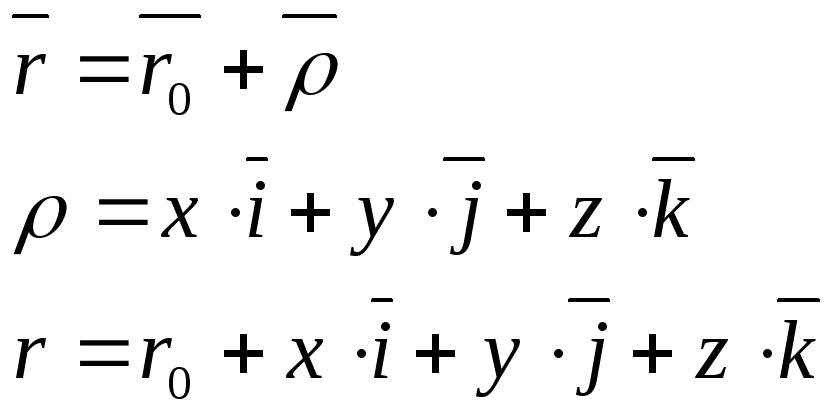 з
рисунка
з
рисунка
i,j,k-орты подвижной системы
перейдем к записи для выражения скоростей:
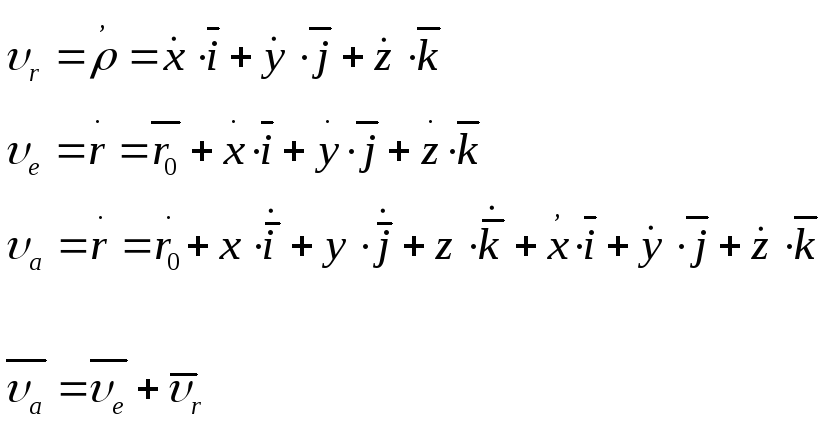
![]()
6) Теорема о сложении ускорений (т.Кориолиса)
Абсолютное ускорение точки равно векторной сумме относительного переносного и Кориолисово ускорение.
![]()
Получим теперь выражение для ускорения движущейся точки.
1)![]()
2)
![]()
3)![]()
Сравнивая три формулы мы видим, что в выражении для абсолютного ускорения кроме переносного и относительного входит ещё одна группа слагаемых, которая называется кориолисовым ускорением.
![]() т.е.
т.е.
![]()
Справка: Густав Кориолис (1792-1843) французский механик, описывающий сложное движение точки. Основные его работы, относятся к аналитической механике и динамике машин. Ввел коэффициент ½ в кинетическую энергию.
7)Модуль и направление поворотного ускорения.
Чтобы получить более удобное выражение для кориолисова ускорения воспользуемся формулой Пуассона.
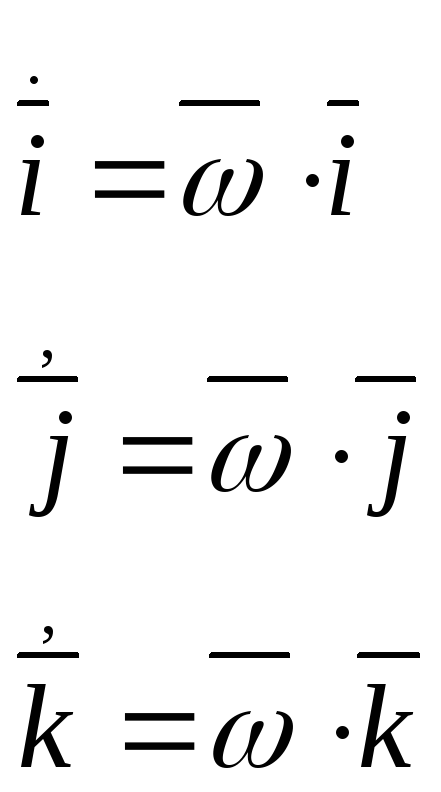
Учитывая, что
угловая скорость переносного движения
![]() .
.
Тогда
![]()
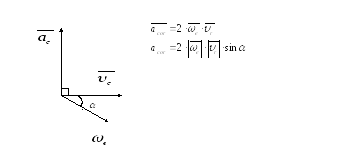
Кориолисова ускорение равно удвоенному векторному произведению угловой скорости переносного движения на относительную скорость точки.
Модуль кориолиосова ускорения:
![]()
Из формулы следует, что кориолисово ускорение может быть равно нулю в трёх случаях.
-
Когда угловая скорость переносного движения равно We,т.е. когда переносное движение является поступательным.
-
Когда относительная скорость точки равно Ur,т.е. когда отсутствует относительное движение.
-
Когда векторы We ,Wr параллельны друг другу ,т.е. когда точка движется вдоль оси вращения.
Направления кориолисова ускорения. Правило Жуковского:
Для того, чтобы найти направления кориолисова ускорения, следует спраекцировать вектор относительно скорости на плоскость, перпендикулярно оси вращения, и затем повернуть эту проекцию на 90 градусов по ходу вращения.

Физический смысл ak (кориолисова ускорения)
-
изменение переносной скорости из-за относительного перемещения точки.
-
Изменение относительной скорости из-за переносного движения подвижной системы отсчета.
Справка: Николай Егорович Жуковский(1847-1921) русский механик, математик «отец русской авиации», основные работы в области аэродинамики, гидродинамики, теория дифференциальных уравнений.
