Тема 2 Оценка структурной и временной сложности программ Алгоритмическая сложность

Понятие алгоритмической сложности

Информацию можно записывать разными способами. Иногда удобнее записать «повторить n раз» вместо того, чтобы писать повторяющуюся последовательность одинаковых знаков. Иногда последовательность бывает сложная и невозможно выделить повторяющуюся часть.

Если в качестве объектов будем рассматривать произвольные последовательности символов из некоторого алфавита, то наиболее экономичным способом их описания будет алгоритмический.

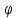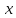Пусть - произвольная частично-рекурсивная функция. Тогдамерой сложности последовательности назовём величину

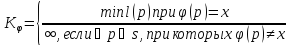
где – программа (код), по которой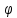восстанавливает последовательность;

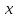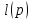–длина такой программы (количество двоичных разрядов);

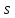–множество всех допустимых программ;

За меру сложности произвольной последовательности символов из некоторого фиксированного алфавита принимается длина (количество двоичных разрядов) самой короткой программы, генерирующей эту последовательность.

Свойства алгоритмической сложности

Свойство 1: Сложность последовательности не превосходит её длины.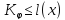

Свойство 2: Сложность последовательности неограниченно растет с увеличением её длины.

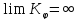
Свойство 3: Подавляющее число последовательностей (почти все) несжимаемы, т.е. случайны.

Свойство 4: Функция К_Y невычисляема, т.е. не существует алгоритма её определения для произвольной символьной последовательности, однако существует общий способ оценки этой величины сверху.

Пусть S – количество символов в алфавите, а N – общее их число в некоторой произвольной последовательности, причем символ с номером l(l = 1, 2, …, s) появляется в ней m_i раз:

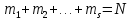
Число всевозможных последовательностей

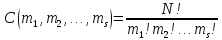
Из свойства 1: Алгоритмическая сложность любой из этих последовательностей не может превосходить количества двоичных разрядов, необходимых для записи их порядковых номеров, иными словами: сложность последовательности не превосходит энтропию произвольной последовательности длины :

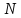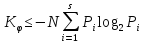
Алгоритмическая сложность любой последовательности не превосходит её энтропии, которую можно найти, определив частоты (вероятности) символов в последовательности

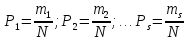
При какой величине алфавита s максимум энтропии H произвольной последовательности из N символов минимален?

Нас интересует минимаксное значение выражения

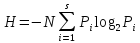
Энтропия 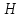имеетмаксимум, когда все символы в последовательности равновероятны.

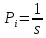
Тогда .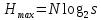

не может быть меньше 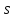, так как каждый символ алфавита должен появиться в последовательности хотя бы раз. Значит, наименьшее значение энтропии будет.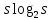

Требуется определить значение , при котором приращение энтропии было бы минимально.

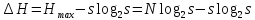
Максимум энтропии минимален при .

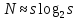Подставляя значение n, получим .

Верхняя оценка уровня алгоритмической сложности:

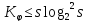
Метрики структурной сложности программ Понятие структурной сложности программы

Структурная сложность программ определяется:

• Числом взаимодействующих компонентов

• Числом связей между компонентами

• Сложностью взаимодействием компонентов (количество связей)

Разнообразие поведения программы и связей между её входными и результирующими данными определяется набором маршрутов (чередующихся последовательностей вершин и дуг графа управления), по которым выполняется программа.

Сложность программного модуля связана не столько с размером (числом команд) программы, сколько с числом маршрутов её исполнения и сложностью.

Маршруты возможной обработки данных определяют сложность разработки программы.

Данную метрику сложности можно использовать для оценки трудоёмкости тестирования и сопровождения модуля, а также для оценки потенциальной надежности его функционирования.

Маршруты исполнения программного модуля подразделяются на:

• Вычислительные маршруты

• Маршруты принятия логических решений

Сложность вычисления маршрутов оценивается формулой:

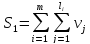
m – количество маршрутов выполнения программы,

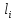–число данных, обрабатываемых в i-ом маршруте

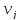–число значений, обрабатываемых данных j-ого типа (2 ≤ 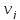≤ 5)

Общее количество арифметических операций не выходит за пределы 5-10%, поэтому вычислительные маршруты определяют структурную сложность программы.

Сложность маршрутов принятия логических решений оценивается формулой

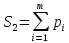
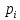–число ветвлений или число проверяемых условий в i-ом маршруте.

Общая сложность программы

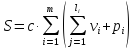
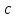–коэффициент пропорциональности.