
Содержание работы:
-
Номенклатура и разграфка топографических карт;
-
Определение прямоугольных и географических координат точек;
-
Измерение расстояний;
-
Измерение ориентирных углов линий;
-
Передача дирекционного угла на последующую линию;
-
Определение отметок точек;
-
Построение профиля линии;
-
Вычисление площади многоугольника.
Задание 1.1. Номенклатура и разграфка топографических карт.
Определить номенклатуру листов карт масштабов 1:1 000 000, 1:100 000, 1:50 000, 1:25 000, на которых находится точка с заданными географическими координатами: широта φ и долгота λ. Нарисовать схему разграфки этих листов.
N-97 широта 63o 54` φ и долгота 156 o 07` λ
Определить номенклатуру и нарисовать схему расположения восьми листов карт масштаба 1:25 000, соседних с листом карты этого масштаба, на котором находится точка с заданными координатами.
Пункт 1.1.1. Определение номенклатуры листа карты.
680 640 P
- 57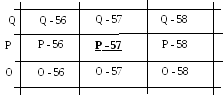



640
600
560 600 1:1
000 000
1500 1560 1620 1680 1620 1560
P
- 57
12 11 10 9 8 7 6 5 4 3 2 1 640













24 13 P
– 57
- 1
36 25 630 640
00’


48 37

60 49
72 61
84 73 620
96 85 630
40’
108 97 1560 1560
30’

120 109 610 1:100
000
40’
132 121 20’

144 143 142 141 140 139 138 137 136 135 134 133 600
1560 1570 1580 1590 1600 1610 1620 30’ 30’
1:1
000 000 P
– 57
–1 - А
P
– 57
- 1 640
00’



630
50’
1560 1560 1560
30’ 1560
15’ 1:50
000 15’
1:100
000 P
– 57
–1 – А - в
P
– 57
–1 - А
630
55’


640
00’ а б



630
55’
в г
630
50’
1560 1560
15’ 630
50’ 7’30”

1:50
000 1560 1:25
000 156007’30”
Рисунок 3 – Выполнение пункта 1.1.1 N-97 (φ=630 54’ λ=156007’)
Пункт 1.1.2 Определение номенклатуры соседних листов.
156007’30” 157015’
1560 155052’30”
640
00’




P
– 56
–12
– Б - б P
– 57
–1
– A
- а P–
57
–
1 – А - б
630
55’

P
– 57
–1
– А - в P
– 56
–12
– Б - г P
– 57
–1 – А - г
630
50’

P
– 56
–24
– Г - б P
– 57
–1 – В - а P
– 57
–1 – В - б
630
45’

Рисунок 4 – Выполнение пункта 1.1.2 N-97
Задание 1.2. Определение прямоугольных и географических координат точек по карте.
Нанести на карту две точки (номера 1 и 2) по их прямоугольным координатам X и Y и две точки (номера 3 и 4) – по их географическим координатам φ и λ. Значения координат по вариантам приведены: для карт масштаба 1:25 000 – в таблице 2 и 3.
Определить φ и λ точек 1 и 2 и X и Y точек 3 и 4.
Пункт 1.2.1. Нанесение точки на карту по координатам X и Y.
-
Определить квадрат координатной сетки, внутри которого находится точка; для этого нужно взять десятки и единицы километров координаты Χ и через тире приписать к ним десятки и единицы координаты Y; все построения точки следует выполнять внутри найденного квадрата;
-
С помощью линейного масштаба установить на циркуле-измерителе расстояние ΔX, равное сотням, десяткам и единицам метров координаты X, и отложить его от основания квадрата вверх на обоих сторонах квадрата; соединить полученные точки тонкой линией карандашом;
-
С помощью линейного масштаба установить на циркуле-измерителе расстояние ΔY, равное сотням, десяткам и единицам метров координаты Y, и отложить его от западной стороны квадрата вправо на обоих основаниях квадрата; соединить полученные точки тонкой линией карандашом;
-
Обвести точку пересечения линий окружностью диаметром 2 – 3 мм и подписать название (номер) точки.
Примечание: Если длина отрезков ΔX или ΔY на карте меньше 4 мм, то удобнее откладывать их дополнения до 1000 м от противоположной стороны квадрата.
Таблица 2 - Варианты задания 1.2 ( для карт масштаба 1:25 000).
|
Номенклатура листа карты |
К О Р Д И Н А Т Ы Т О Ч Е К 1 И 3 |
|||
|
Координаты точки 1 |
Координаты точки 3 |
|||
|
X (м) |
Y (м) |
широта φ |
долгота λ |
|
|
Снов У-34-37-В-в |
6 065 100 |
4 313 400 |
540 40’ 12”
|
180 07’04” |
Координаты точек 2 и 4 вычисляются по формулам
Точка 2
X2 = X1 + 300м – 25м . e
6065100+300-(25*7) = 6065225м
Y2 = Y1 +825м -50м. e
4313400+825-(50*7) = 4313875м
Точка 4
φ4 = φ3 - 1". e
540 40’ 12” - 7" = 540 40’ 05”
λ4 = λ3 - 40"- 2". e
180 07’04” - 54" = 180 06’10”
Пункт 1.2.2 Определение координат X и Y точки по карте.
-
Записать координату X (в км) юго-западного угла квадрата, в котором располагается точка;
-
С помощью циркуля-измерителя и линейного масштаба измерить расстояние ΔX в метрах (сотни, десятки и единицы) от точки до основания квадрата и приписать его к записанной координате;
-
Записать координату Y (в км) юго-западного угла квадрата, в котором располагается точка;
-
С помощью циркуля-измерителя и линейного масштаба измерить расстояние ΔY в метрах (сотни, десятки и единицы) от точки до западной стороны квадрата и приписать его к записанной координате;
Пункт 1.2.3. Нанесение точки на карту по географическим координатам широте φ и долготе λ.
-
Отложить на западной и восточной минутных рамках значение широты точки с точностью до секунды;
-
Соединить полученные точки тонкой прямой линией (через всю карту) – это будет параллель точки;
-
Отложить на южной и северной минутных рамках значение долготы точки с точностью до секунды;
-
Соединить полученные точки тонкой прямой линией (через всю карту) – это будет меридиан точки;
-
Обвести точку пересечения параллели и меридиана точки окружностью диаметром 2 – 3 мм и подписать название (номер) точки.
Пункт 1.2.4. Определение широты и долготы точки по карте.
-
Используя минутные рамки широты, провести две параллели через 10” так, чтобы точка оказалась между ними;
-
Отсчитать широту точки с точностью до секунд (секунды определяются на глаз);
-
Используя минутные рамки долготы, провести два меридиана через 10” так, чтобы точка оказалась между ними;
-
Отсчитать долготу точки с точностью до секунд (секунды определяются на глаз.
Таблица 3 – Выполнение задания 1.2 N-97
Масштаб карты 1:25 000
|
Номер Точки |
Прямоугольные координаты |
Географические координаты |
||
|
X (м) |
Y (м) |
широта φ |
долгота λ |
|
|
1 |
6 065 100 |
4 313 400 |
540 40’ 32” |
180 06’ 27” |
|
2 |
6 065 225 |
4 313 875 |
540 40’ 39” |
180 06’ 51” |
|
3 |
6 064 400 |
4 314 075 |
540 40’ 12” |
180 07’ 04” |
|
4 |
6 064 250 |
4 313 100 |
540 40’ 05” |
180 06’ 10” |
Задание 1.3. Измерение расстояний на карте.
Перед выполнением задания нужно построить на карте четырёхугольник 1-2-3-4, соединив последовательно точку 1 с точкой 2, точку 2 с точкой 3, точку 3 с точкой 4 и точку 4 с точкой 1. Каждую сторону четырёхугольника рекомендуется продолжить за их граничные точки на 4 - 5 см.
Измерить все четыре стороны четырёхугольника с помощью линейного масштаба и с помощью поперечного масштаба.
Пункт 1.3.1. Измерение расстояния с помощью линейного масштаба.
- Зафиксировать длину линии циркулем-измерителем;
-
Поставить одну иглу циркуля на целое основание справа от нуля; взять отсчёт справа от нуля по этому основанию;
-
По положению другой иглы взять отсчёт слева от нуля;
-
Сложить оба отсчёта.
П ример
измерения линии показан на рисунке 8.
ример
измерения линии показан на рисунке 8.
0 1 1000 200 400 600 800 км










Рисунок 8 – Пример выполнения пункта 1.3.1; S= 1000 м + 560 м = 1560 м
Пункт 1.3.2. Измерение расстояния с помощью поперечного масштаба.
-
Подписать поперечный масштаб в соответствии с линейным масштабом карты (1:50 000 – в 1 см 500 м): каждое основание (a=2 см) справа от нуля через 1 км; слева от нуля каждое деление (2 мм) через 100 м; каждое деление вверх – через 10 м;
-
Зафиксировать длину линии циркулем-измерителем.
-
Одну иглу циркуля поставить на целое основание справа от нуля; другую иглу – на любую трансверсаль; при этом обе иглы должны располагаться на линии, параллельной нижней линии оснований;
-
Взять 3 отсчёта: N1 – по целому основанию, N2 – по основанию трансверсали, N3 – вверх по линии, соединяющей иглы циркуля.
-
Сложить все три отсчёта.
Пример выполнения пункта 1.3.2 показан на рисунке 9.



100
80









60
40



20

1000
м 200 600 0 1
км 2
км 3
км


400 800
Рисунок 9 – Пример выполнения пункта 1.3.2 (S= 1 км + 500м + 70м = 1570м)
Точность измерения расстояний с помощью графических масштабов оценивается половиной наименьшего деления (линейный масштаб – 25 м; поперечный масштаб – 5 м при масштабе 1:50 000).
Пример выполнения задания 1.3 приведён в таблице 3.
