32. Сформулируйте принцип Гюйгенса-Френеля. Как строятся зоны Френеля в случае дифракции на круглом отверстии? Какой вид имеет дифракционная картина в этом случае?

Принцип Гюйгенса-Френеля: Каждый элемент волнового фронта можно рассматривать, как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Дифракция от круглого отверстия. Поставим на пути сферической световой волны непрозрачный экран с вырезанным в нем круглым отверстием радиуса r₀. Расположим экран так, чтобы перпендикуляр, опущенный из источника света S, попал в центр отверстия. На продолжении этого перпендикуляра возьмем точку Р. Если расстояния a и b удовлетворяют соотношению

,

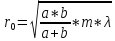то отверстие оставит открытыми ровно m первых зон Френеля, построенных для точки P. Следовательно, число открытых зон Френеля определяется выражением

.

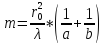Амплитуда в точке P будет равна

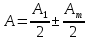(знак плюс берется для нечетных m, минус – для четных m).

Для малых m амплитуда A_m мало отличается от A₁. Следовательно, при нечетных m амплитуда в точке P будет приближенно равна A₁ при четных m – нулю.

Если убрать преграду, амплитуда в точке P станет равной 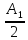. Таким образом, преграда с отверстием, открывающим небольшое нечетное число зон, не только не ослабляет освещенность в точке P, но, напротив, приводит к увеличению амплитуды почти в два раза, а интенсивности – почти в четыре раза.

Характер дифракционной картины, которая будет наблюдаться на экране, помещенном за преградой. Вследствие симметричного расположения отверстия относительно прямой SP освещенность в разных точках экрана будет зависеть только от расстояния r от точки P. В самой этой точке интенсивность будет достигать максимума или минимума в зависимости от того, каким – четным или нечетным – будет число открытых зон Френеля.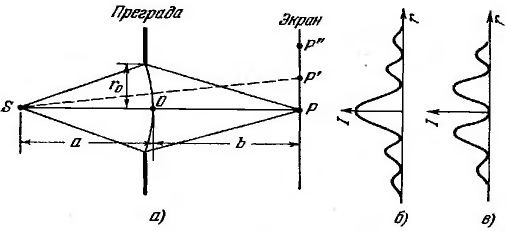

Дифракционная картина от круглого отверстия имеет вид чередующихся светлых и темных концентрических колец. В центре картины будет либо светлое (m нечетное), либо темное (m четное) пятно. Ход интенсивности I с расстоянием r от центра картины изображен на рисунке б (для нечетного m) и на рисунке в (для четного m). При перемещении экрана параллельно самому себе вдоль прямой SP картины, будут сменять друг друга.

Если отверстие открывает лишь часть центральной зоны Френеля, на экране получается размытое светлое пятно; чередования светлых и темных колец в этом случае не возникает. Если отверстие открывает большое число зон, чередование светлых и темных колец наблюдается лишь в очень узкой области на границе геометрической тени; внутри этой области освещенность оказывается практически постоянной.

33. Как строятся зоны Френеля в случае дифракции на щели? Как выглядит ди­фракционная картина Френеля в случае дифракции на щели?

Дифракция от щели. Задача о дифракции Френеля от щели может быть решена с помощью спирали Корню. Волновую поверхность падающего света, плоскость щели и экран, на котором наблюдается дифракционная картина, будем считать параллельными друг другу.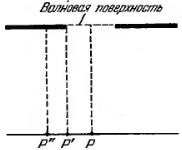

Для точки P, лежащей против середины щели, начало и конец результирующего вектора находятся в симметричных, относительно начала координат, точках спирали. Если сместиться в точку P', лежащую против края щели, начало результирующего вектора переместится в середину спирали О. Конец вектора переместится по спирали в направлении полюса F₁. При углублении в область геометрической тени начало и конец результирующего вектора будут скользить но спирали и в конце концов окажутся на наименьшем расстоянии друг от друга. Интенсивность света достигнет при этом минимума. При дальнейшем скольжении по спирали начало и конец вектора снова отойдут друг от друга и интенсивность будет расти. То же самое будет происходить при смещении из точки P в противоположную сторону, так как дифракционная картина симметрична относительно середины щели.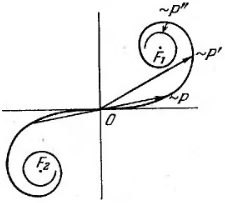

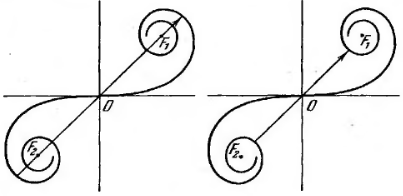
Если изменять ширину щели, сдвигая полуплоскости в противоположные стороны, интенсивность в средней точке P будет пульсировать, проходя попеременно через максимумы и отличные от нуля минимумы.

Дифракционная картина от щели представляет собой либо светлую, либо относительно темную центральную полосу, по обе стороны которой располагаются симметричные относительно нее чередующиеся темные и светлые полосы.

34. Дифракция на больших расстояниях от преграды. Как выглядит дифракционная картина Фраунгофера в случае дифракции на щели? Что получится, если имеется система одинаковых периодически распо­ложенных щелей?

Дифракция Фраунгофера – случай дифракции, при которой дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Расстояние должно быть таким, чтобы можно было пренебречь в выражении для разности фаз членами порядка 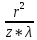(z – расстояние от отверстия или преграды до плоскости наблюдения; λ – длина волны излучения, r – радиальная координата рассматриваемой точки в плоскости наблюдения в полярной системе координат), что сильно упрощает теоретическое рассмотрение явления. Иными словами, дифракция Фраунгофера наблюдается тогда, когда число зон Френеля m<<1, при этом приходящие в точку волны являются практически плоскими.

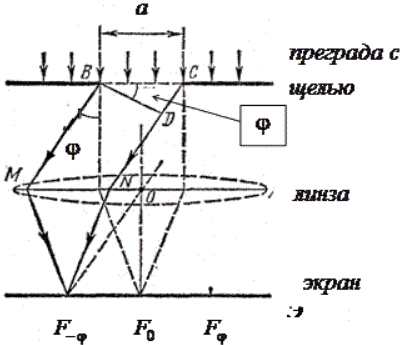
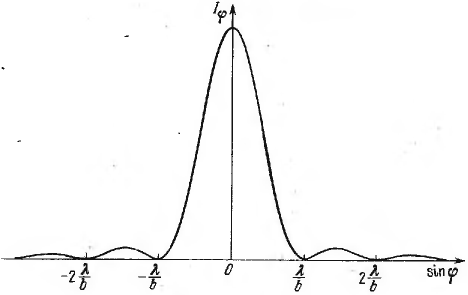
Дифракция Фраунгофера от щели. Параллельный пучок монохроматического света падает нормально на непрозрачную преграду, в которой прорезана узкая щель ВС, имеющая постоянную ширину и длину. В соответствии с принципом Гюйгенса-Френеля точки щели являются вторичными источниками волн, колеблющимися в одной фазе, так как плоскость щели совпадает с фронтом падающей волны. При дифракции Фраунгофера на щели для дифракционной картины на экране наблюдений имеем: условие минимума: 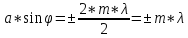; условие максимума: 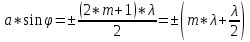. Угловая ширина центрального максимума равна .

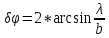Дифракционная решётка. Выясним характер дифракционной картины, получающейся на экране при падении на решетку плоской световой волны. Каждая из щелей даст на экране картину. Картины от всех щелей придутся на одно и то же место экрана. Если бы колебания, приходящие в точку Р от различных щелей, были некогерентными, результирующая картина от N щелей отличалась бы от картины, создаваемой одной щелью, лишь тем, что все интенсивности возросли бы в N раз. Однако колебания от различных щелей являются в большей или меньшей степени когерентными; поэтому результирующая интенсивность будет отлична от .

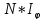Будем предполагать, что радиус когерентности падающей волны намного превышает длину решетки, так что колебания от всех щелей можно считать когерентными друг относительно друга. В этом случае результирующее колебание в точке Р, положение которой определяется углом φ, представляет собой сумму N колебаний с одинаковой амплитудой A_φ, сдвинутых друг относительно друга по фазе на одну и ту же величину δ. Интенсивность при этих условиях равна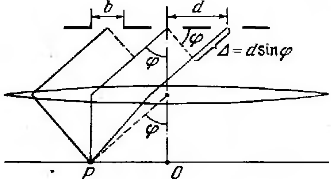

.

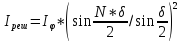Видно, что разность хода от соседних щелей равна 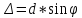. Следовательно, разность фаз

.

Получим

.

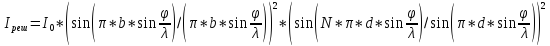Первый множитель обращается в нуль в точках, для которых 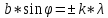(k=1, 2, 3, …).

В этих точках интенсивность, создаваемая каждой из щелей в отдельности, равна нулю.

Второй множитель в принимает значение N² в точках, для которых 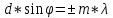(m=0, 1, 2, …).

Для направлений, определяемых этим условием, колебания от отдельных щелей взаимно усиливают друг друга, вследствие чего амплитуда колебаний в соответствующей точке экрана равна

.

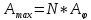Возведя равенство в квадрат, получим, что интенсивность главных максимумо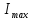в в 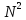раз больше интенсивности 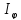, создаваемой в направлении φ одной щелью:

.

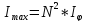Кроме минимумов в промежутках между соседними главными максимумами имеется (N—1) добавочных минимумов. Эти минимумы возникают в тех направлениях, для которых колебания от отдельных щелей взаимно погашают друг друга. Направления добавочных минимумов определяются условием

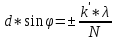(k'≠0, N, 2*N, …).