30. Какие волны называются когерентными? Как их получить? Какова ширина ин­терференционных полос в опыте Юнга? Как влияют размеры источника на ин­терференционную картину?

Когерентные волны – волны, имеющие одинаковые частоты, постоянную разность фаз, а колебания происходят в одной плоскости.

Можно получить: 1) "вырезая" из спонтанного излучения обычного источника часть, содержащую возможно более узкий диапазон длин волн и имеющую возможно более простой волновой фронт. Пример реализации - газоразрядная лампа с узкополосным светофильтром и точечной диафрагмой; 2) формируя параметры излучения при его возникновении, делая излучение "вынужденным". Пример реализации - лазер.

.

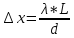Протяженный источник состоит из большого числа точечных взаимно некогерентных элементов. Поэтому интенсивность в любом месте равна сумме интенсивностей в интерференционных картинах, создаваемых отдельными точечными элементами источника.

В интерференционных опытах по методу деления волнового фронта полосы на экране перпендикулярны плоскости, в которой находятся первичный точечный источник S и вторичные источники S1 и S2. Использование вместо S линейного источника, т.е. достаточно узкой щели, вытянутой перпендикулярно этой плоскости, увеличивает интенсивность и не приводит к ухудшению четкости интерференционных полос. Однако увеличение ширины щели приводит к тому, что полосы становятся менее четкими или пропадают совсем.

Если размеры источника (т.е. ширина щели S) много меньше длины световой волны, то интерференционная картина будет резкой, так как разность хода интерферирующих лучей от любой точки источника до некоторой точки наблюдения P будет практически одна и та же. Но обычно размеры источника значительно больше длины волны, поэтому одинаковые интерференционные картины от разных его элементов сдвинуты одна относительно другой. В результате наложения этих картин интерференционные полосы оказываются более или менее размытыми. Их можно наблюдать лишь при выполнении определенных условий, налагаемых на геометрию эксперимента. Эти условия подробно обсуждаются ниже.

31. Опишите явление интерференции в тонкой плёнке. Как изменяется наблюдае­мая картина при изменении толщины плёнки?

Плоскопараллельная пластинка. Обе плоские отраженные волны распространяются в одном направлении, образующем с нормалью к пластинке угол, равный углу падения θ₁. Эти волны смогут интерферировать, если будут соблюдены условия как временной, так и пространственной когерентности.

Для того чтобы имела место временная когерентность, разность хода не должна превышать длину когерентности; равную 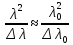. Следовательно, должно соблюдаться условие

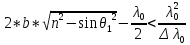или

.

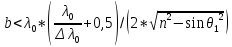В полученном соотношении половиной можно пренебречь по сравнению с 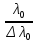. Выражение 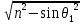имеет величину порядка единицы. Поэтому можно написать

.

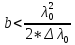(удвоенная толщина пластинки должна быть меньше длины когерентности).

Положив 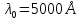и 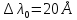, получим предельное значение толщины, равное



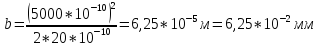
Теперь рассмотрим условия соблюдения пространственной когерентности. Поставим на пути отраженных пучков, экран. Приходящие в точку Р' лучи 1' и 2' отстоят в падающем пучке на расстояние ρ'. Если это расстояние не превышает радиуса когерентности ρ_ког падающей волны, лучи 1' и 2' будут когерентными и создадут в точке P' освещенность, определяемую значением разности хода Δ, отвечающим углу падения θ₁'. Другие пары лучей, идущие под тем же углом θ₁', создадут в остальных точках экрана такую же освещенность. Таким образом, экран окажется равномерно освещенным. При изменении наклона пучка освещенность экрана будет меняться.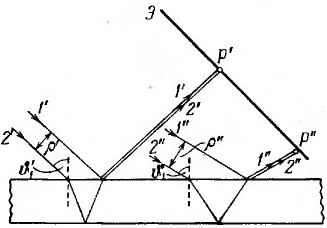

Видно, что расстояние между падающими лучами 1 и 2 равно



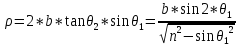
Если принять n=1,5, то для θ₁=45° получается ρ=0,8*b, а для θ₁= 10° – ρ=0,1*b. Для нормального падения ρ=0 при любом n.

Пластинка переменной толщины. Возьмем пластинку в виде клина с углом при вершине φ. Пусть на нее падает параллельный пучок лучей. Теперь лучи, отразившиеся от разных поверхностей пластинки, не будут параллельными. Два до падении на пластинку практически сливающихся луча 1' пересекаются после отражения в точке Q'. Два практически сливающихся луча 1" пересекаются в точке Q". Можно показать, что точки Q, Q' и другие аналогичные им точки лежат в одной плоскости, проходящей через вершину клина О. Отразившийся от нижней поверхности клина луч 1' и отразившийся от верхней поверхности луч 2' пересекутся в точке R', расположенной ближе к клину, чем Q'. Аналогичные лучи 1' и 3' пересекутся в точке P' отстоящей от поверхности клина дальше, чем О'.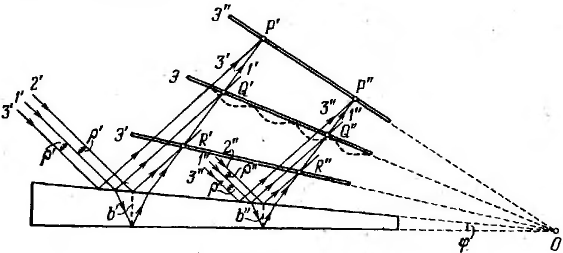

Направления распространения волн, отраженных от верхней и нижней поверхностей клина, не совпадают. Временная когерентность будет соблюдаться только для частей волн, отразившихся от мест клина, для которых толщина удовлетворяет условию 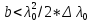. Допустим, что это условие выполняется для всего клина. Кроме того, предположим, что радиус когерентности намного превышает длину клина. Тогда отраженные волны будут когерентными во всем пространстве над клином, и при любом расстоянии экрана от клина на нем будет наблюдаться интерференционная картина в виде полос, параллельных вершине клина О. Так, в частности, обстоит дело при освещении клина светом испускаемым лазером.

Если расположить экран так, чтобы он проходил через точки Q', Q", ..., на экране возникнет интерференционная картина даже в том случае, если пространственная когерентность падающей волны крайне мала. При малом угле клина разность хода лучей можно с достаточной степенью точности вычислять по формуле 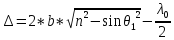, беря в качестве b толщину пластинки в месте падения на нее лучей. Поскольку разность хода для лучей, отразившихся от различных участков клина, теперь неодинакова, освещенность экрана будет неравномерной – на экране появятся светлые и темные полосы (пунктирная кривая). Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, вследствие чего их называют полосами равной толщины.

При смещении экрана из положения Э в направлении от клина или к клину начинает сказываться степень пространственной когерентности падающей волны. Если в положении экрана, Э' расстояние ρ' между падающими лучами 1' и 2' станет порядка радиуса когерентности, интерференционная картина на экране Э' наблюдаться не будет. Аналогично картина исчезает в положении экрана, обозначенном через Э".