35. Что называется разрешающей способностью дифракционной решётки? Что называется дисперсией дифракционной решётки? Как они связаны с парамет­рами решётки?

Разрешающая способность (предел разрешения) – минимальное расстояние, при котором два близко расположенные точечные предмета будут изображаться как раздельные.

Разрешающая способность дифракционной решётки характеризует возможность раздельного наблюдения двух спектральных линий, имеющих близкие волны.

.

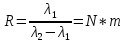Дисперсия:

угловая: .

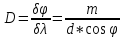(δφ – угловое расстояние между спектральными линиями, отличающимися по длине волны на δλ).

линейная: .

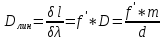(δl – линейное расстояние на экране или фотопластинке между спектральными линиями, отличающимися по длине волны на δλ).

36. Как наблюдать дифракцию рентгеновских лучей? Выведите формулу Вульфа-Врэгга.

Дифракция рентгеновских лучей. Вопрос о том, каким образом лучи, идущие от различных структурных элементов, сводятся в одну точку экрана в случае видимого света это решается с помощью линзы. Для рентгеновских лучей осуществить линзу нельзя, так как показатель преломления этих лучей во всех веществах практически равен единице. Поэтому интерференция вторичных волн достигается путем использования весьма узких пучков лучей, которые и без линзы дают на экране пятна очень малых размеров.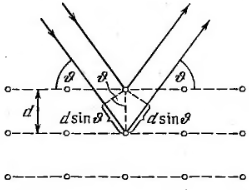

Проведем через узлы кристаллической решетки параллельные равноотстоящие плоскости, которые мы будем называть атомными слоями. Если падающая на кристалл волна плоская, огибающая вторичных волн, порождаемых атомами, лежащими в таком слое, также будет представлять собой плоскость. Таким образом, суммарное действие атомов, лежащих в одном слое, можно представить в виде плоской волны, отразившейся от усеянной атомами поверхности по обычному закону отражения.

Плоские вторичные волны, отразившиеся от разных атомных слоев, когерентны и будут интерферировать между собой подобно волнам, посылаемым в данном направлении различными щелями дифракционной решетки. При этом, как и в случае решетки, вторичные волны будут практически погашать друг друга во всех направлениях, кроме тех, для которых разность хода между соседними волнами является кратной λ. Видно, что разность хода двух волн, отразившихся от соседних атомных слоев, равна 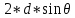. Следовательно, направления, в которых получаются дифракционные максимумы, определяются условием 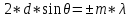(m=1, 2, …). Это соотношение называется формулой Брэгга-Вульфа.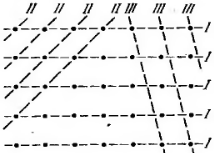

Атомные слои в кристалле можно провести множеством способов. Каждая система слоев может дать дифракционный максимум. Однако заметную интенсивность имеют лишь те максимумы, которые получаются за счет отражений от слоев, достаточно густо усеянных атомами.

37. Покажите с помощью формул Френеля, что степень поляризации света при от­ражении изменяется. Когда отражённый свет оказывается полностью поляри­зованным? Каково при этом направление поляризации отражённого света?

Если угол падения света на границу раздела двух диэлектриков отличен от нуля, отраженный и преломленный лучи оказываются частично поляризованными. В отраженном луче преобладают колебания, перпендикулярные к плоскости падения, в преломленном луче – колебания, параллельные плоскости падения. Степень поляризации зависит от угла падения.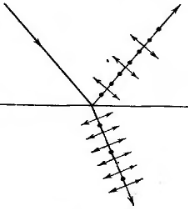

Обозначим через θ_пр угол, удовлетворяющий условию 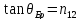. При угле падения θ₁, равном θ_Бр, отраженный луч полностью поляризован. Степень поляризации преломленного луча при угле падения, равном θ_Бр, достигает наибольшего значения, однако этот луч остается поляризованным только частично.

Степень поляризации отраженного и преломленного лучей при различных углах падения можно получить с помощью формул Френеля. Формулы Френеля устанавливают соотношения между комплексными амплитудами падающей, отраженной и преломленной волн. Равенство двух комплексных амплитуд означает равенство как обычных амплитуд, так и начальных фаз обоих колебаний:

.

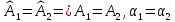В случае, когда комплексные амплитуды отличаются знаком, обычные амплитуды одинаковы, а начальные фазы отличаются на π ().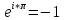

.

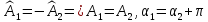Представим падающую волну в виде наложения двух некогерентных волн, в одной из которых колебания совершаются в плоскости падения, а в другой перпендикулярно к этой плоскости. Обозначим:

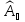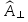и – амплитуды падающих волн;

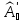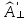и – амплитуды отражённых волн;

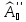и 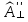– амплитуды преломлённых волн.

Формулы Френеля имеют следующий вид*:

;

;

;

;

.

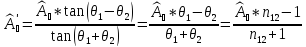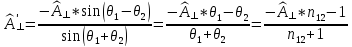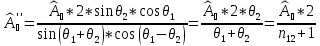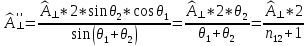Возведя уравнения в квадрат и умножив получившиеся выражения на показатель преломления соответствующей среды, получим соотношения между интенсивностями падающего, отраженного и преломленного лучей для случая малых углов падения.

;

.
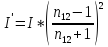
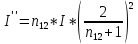