ЭКЗАМЕН ЭЛЕКТРОМАГНЕТИЗМ И ОПТИКА.

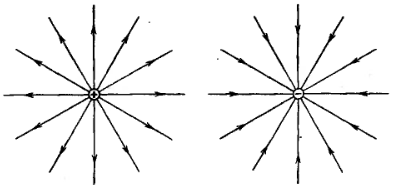
1. Что называется точечным зарядом? Сформулируйте закон сохранения элек­трического заряда. Сформулируйте закон Кулона. Дайте определение напря­жённости электрического поля. Какова напряжённость поля, созданного то­чечным зарядом на расстоянии r от него? Сформулируйте принцип суперпози­ции для электрического поля. Как изображается электрическое поле? Как вы­глядят силовые линии точечного заряда?

Электрический заряд является неотъемлемым свойством некоторых элементарных частиц. Заряд всех элементарных частиц (если он не равен нулю) одинаков по абсолютной величине. Его можно назвать элементарным зарядом.

q.

Закон сохранения электрического заряда: суммарный заряд электрически изолированной системы не может изменяться.

.

Закон Кулона: сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними. Направление силы совпадает с соединяющей заряды прямой.

.

Напряжённость электрического поля – векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы, действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда.

.

.

Принцип суперпозиции (наложения) электрических полей: напряженность поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности.

2. Дайте определение потока вектора напряжённости электрического поля. Сфор­мулируйте теорему Гаусса. Найдите с её помощью напряжённость электриче­ского поля равномерно заряженной сферы, бесконечной нити и бесконечной плоскости, объемно-заряженного шара.

Поток вектора напряжённости – условное обозначение количества силовых линий поля, проходящих через сечение определённой площади.

.

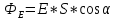Теорема Гаусса: поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на ε₀.

Поле бесконечной однородно заряженной плоскости. Представим себе мысленно цилиндрическую поверхность с образующими, перпендикулярными к плоскости, и основаниями величины ΔS, расположенными относительно плоскости симметрично. Применим к поверхности теорему Гаусса. Поток через боковую часть поверхности будет отсутствовать, поскольку Е_n в каждой ее точке равна нулю. Для оснований Е_n совпадает с Е., следовательно, суммарный поток через поверхность равен 2Е*ΔS. Внутри поверхности заключен заряд σ*ΔS. Согласно теореме Гаусса, должно выполняться условие:

, из которого .

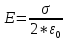Поле бесконечного заряженного цилиндра. Пусть поле создается бесконечной цилиндрической поверхностью радиуса R. Представим себе мысленно коаксиальную с заряженной поверхностью замкнутую цилиндрическую поверхность радиуса r и высоты h. Для оснований цилиндра E_n=0, для боковой поверхности Е_n=Е(r). Следовательно, поток вектора Е через рассматриваемую поверхность равен E(r)*2*π*r*h. Если r>R, внутрь поверхности попадает заряд q=λ*h. Применив теорему Гаусса, получим: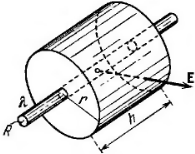

, откуда .

Поле заряженной сферическом поверхности. Поле, создаваемое сферической поверхностью радиуса R. Вообразим концентрическую с заряженной сферой поверхность радиуса r. Для всех точек этой поверхности Е_n=Е(r). Если r>R, внутрь поверхности попадает весь заряд q, распределенный по сфере. Согласно теореме Гаусса:

, откуда .

Вне этой поверхности поле тождественно с полем точечного заряда той же величины, помещенного в центр сферы.

Поле объемно-заряженного шара. Для поля вне шара получается тот же результат, что и в случае поверхностно-заряженной сферы. Сферическая поверхность радиуса r (r<R) заключает в себе заряд, равный ρ*4/3*π*r³. Теорема Гаусса для такой поверхности запишется следующим образом:

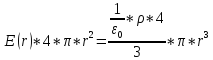, отсюда, заменив ρ на , получим.

3. Какую работу совершает электрическое поле над зарядом при переносе его вдоль замкнутого контура? Дайте определение потенциала электрического поля. Как связаны потенциал и напряжённость? Найдите с помощью этого со­отношения потенциал точечного заряда на расстоянии r от него.

Работа электрического поля, как консервативного, совершается только при переносе заряда вдоль линий действия сил. При возврате заряда в начальное положение работа равна нолю.

Электростатический потенциал – скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля.

.

.

.

4. Что называется электрическим диполем? Найдите потенциал, созданный дипо­лем в точке с радиус-вектором r, начало которого выбрано в середине диполя. Какие силы действуют на диполь в электрическом поле? Какова его потенци­альная энергия?

Электрический диполь – система двух одинаковых по величине разноименных точечных зарядов +q и -q, расстояние между которыми значительно меньше расстояния до тех точек, в которых определяется поле системы. Прямая, проходящая через оба заряда, называется осью диполя.

Это поле обладает осевой симметрией. Поэтому картина поля в любой плоскости, проходящей через ось диполя, будет одной и той же, причем вектор Е лежит в этой плоскости. Положение точки относительно диполя будем характеризовать с помощью радиуса-вектора r либо с помощью полярных координат r и φ. Введем вектор l, проведенный от отрицательного заряда к положительному. Положение заряда +q относительно центра диполя определяется вектором a, заряда -q – вектором -а. Очевидно, что l=2*a. Расстояния до данной точки от зарядов +q и -q обозначим соответственно через r₊ и r_-. Ввиду малости a по сравнению с r можно положить приближенно, что

.

.

.

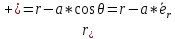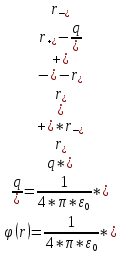Произведение r₊+r_- можно заменить через r². Разность r₊-r_- равна 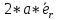. Следовательно,

.

Из рисунка видно, что 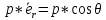, откуда

.

Силы, действующие на диполь в электрическом поле. Если диполь поместить в однородное электрическое поле, образующие диполь заряды +q и -q окажутся под действием равных по величине, но противоположных по направлению сил F₁ и F₂. Момент сил стремится повернуть диполь так, чтобы его электрический момент р установился по направлению поля. Эти силы образуют пару, плечо которой равно а, т. е. зависит от ориентации диполя относительно поля. Модуль каждой из сил равен q*E. Умножив его на плечо, получим величину момента пары сил, действующих на диполь:

.

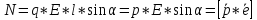Потенциальная энергия диполя во внешнем электрическом поле.

.

.

5. Какой энергией обладает система точечных зарядов?

Энергия взаимодействия системы зарядов. Выражение можно рассматривать как взаимную потенциальную энергию зарядов q и q'. Обозначив заряды через q₁ и q₂, получим для их энергии взаимодействия формулу

.

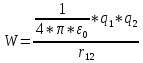Рассмотрим систему, состоящую из N точечных зарядов. Энергия взаимодействия такой системы равна сумме энергий взаимодействия зарядов, взятых попарно:

.

6. Какие тела называются проводниками? Какова напряжённость поля внутри проводника? Как направлены силовые линии на поверхности проводника?

Проводник – вещество, среда, материал, хорошо проводящие электрический ток.

В проводнике имеется большое число свободных носителей заряда, то есть заряженных частиц, которые могут свободно перемещаться внутри объёма проводника и под действием приложенного к проводнику электрического напряжения создают электрический ток.

Напряжённость внутри проводника равна нолю, так как заряды в проводнике способны свободно перемещаться. Потенциалы во всех его точках равны.

Силовые линии на поверхности проводника направлены по нормали к ней. Поверхность проводника является эквипотенциальной.

7. Как связаны напряжённость поля на поверхности проводника и поверхностная плотность зарядов? Как изменяется потенциал вдоль поверхности проводника?

Напряжённость вблизи поверхности проводника равна: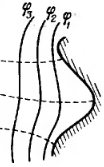

.

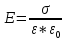При заданном потенциале проводника плотность зарядов определяется кривизной поверхности – она растет с увеличением положительной кривизны (выпуклости) и убывает с увеличением отрицательной кривизны (вогнутости). Особенно велика бывает плотность зарядов на остриях. Поэтому напряженность поля вблизи остриев может быть настолько большой, что возникает ионизация молекул газа, окружающего проводник.

8. Дайте определение ёмкости конденсатора. Вычислите ёмкость плоского, цилиндрического и сфе­рического конденсаторов. Чему равна ёмкость системы последовательно со­единённых конденсаторов? Чему равна ёмкость системы параллельно соеди­нённых конденсаторов?

Электрическая ёмкость – характеристика конденсатора, мера его способности накапливать электрический заряд.

Ёмкость плоского конденсатора. Напряженность поля между обкладками равна

.

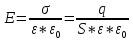Разность потенциалов между обкладками равна

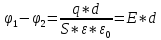, откуда

.

Ёмкость цилиндрического конденсатора. Если пренебречь рассеянием поля вблизи краев обкладок, она равна

.

Емкость сферического конденсатора равна

.

Емкость системы последовательно соединённых конденсаторов.

.

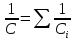Емкость системы параллельно соединённых конденсаторов.

.

С резисторами обратным образом.

9. Какие вещества называются диэлектриками? Дайте определение вектора поля­ризации. Как связаны вектор поляризации и плотность поляризационных заря­дов на поверхности диэлектрика? Как связаны вектор поляризации и объёмная плотность поляризационных зарядов?

Диэлектрики (изоляторы) – вещества, не способные проводить электрический ток. Идеальных изоляторов в природе не существует. Вещества, называемые диэлектриками, проводят ток в 10¹⁵-10²⁰ раз хуже, чем вещества, называемые проводниками.

Вектор поля­ризации диэлектрика – величина, численно равная отношению дипольного момента диэлектрика, возникшего при поляризации, к объёму диэлектрика.

.

Связь между поляризованностью и поверхностной плотностью поляризационных зарядов.

Величина выделенного объема равна

.

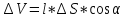Объем имеет дипольный электрический момент

.

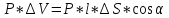С макроскопической точки зрения рассматриваемый объем эквивалентен диполю, образованному зарядам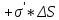и и , электрический момент можно представить в виде .

, откуда

.

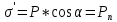Связь между поляризованностью и объёмной плотностью поляризационных зарядов.

При включении поля через площадку ΔS переносится в направлении нормали к ней заряд

.

.

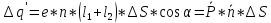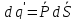Введя объемную плотность связанных зарядов ρ', можно написать

.

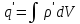(интеграл берется по объему, ограниченному поверхностью S). Таким образом, мы приходим к формуле

.

Преобразуем поверхностный интеграл по теореме Остроградского-Гаусса. В результате получится соотношение

.

Это соотношение должно выполняться для любого произвольно выбранного объема V, что возможно лишь в том случае, если в каждой точке диэлектрика выполняется равенство

.
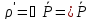