Matlab. Основы работы

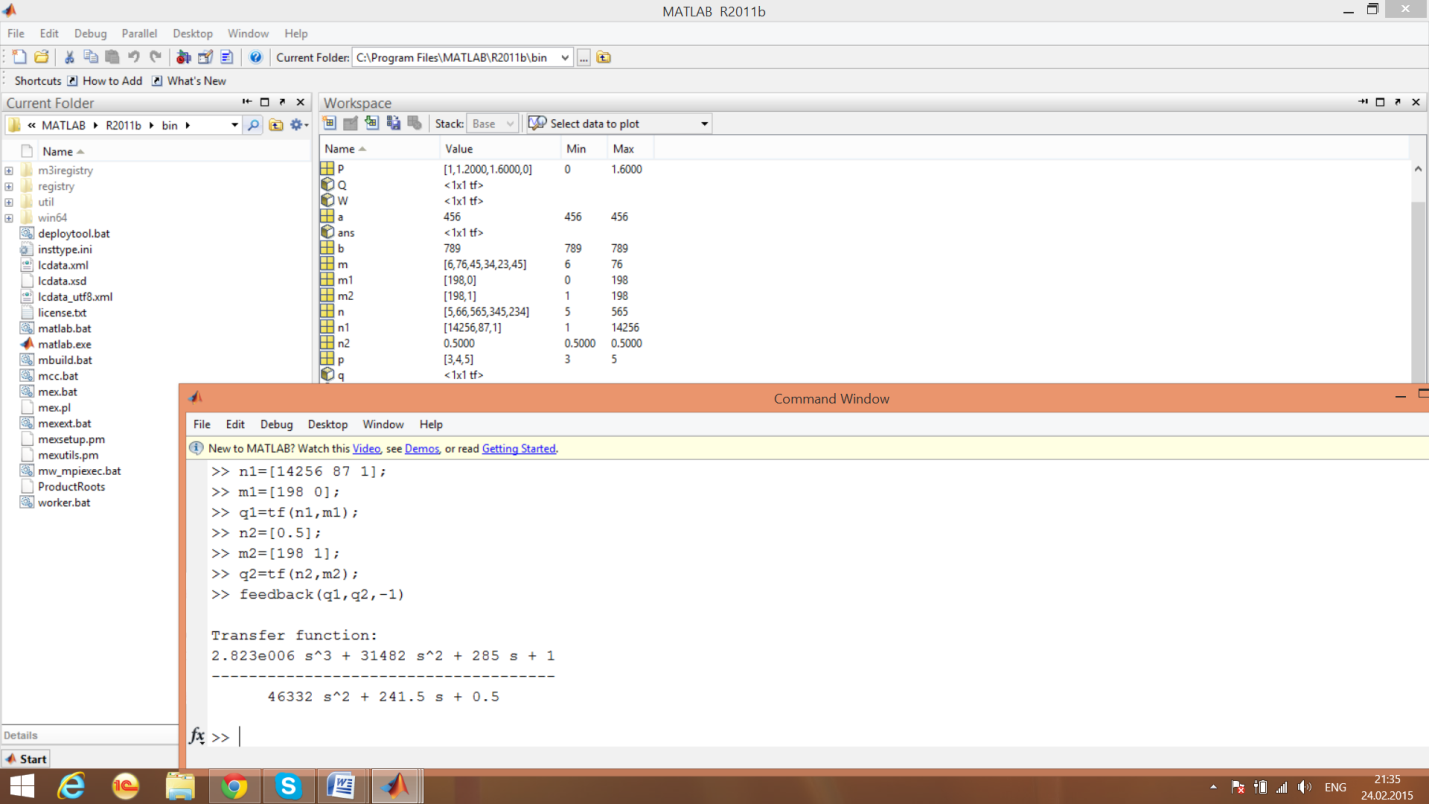
Командное окно MATLAB после выполнения вычислений

. Рабочее пространство пакета MATLAB

Структура рабочего пространства MATLAB, после выполнения команд

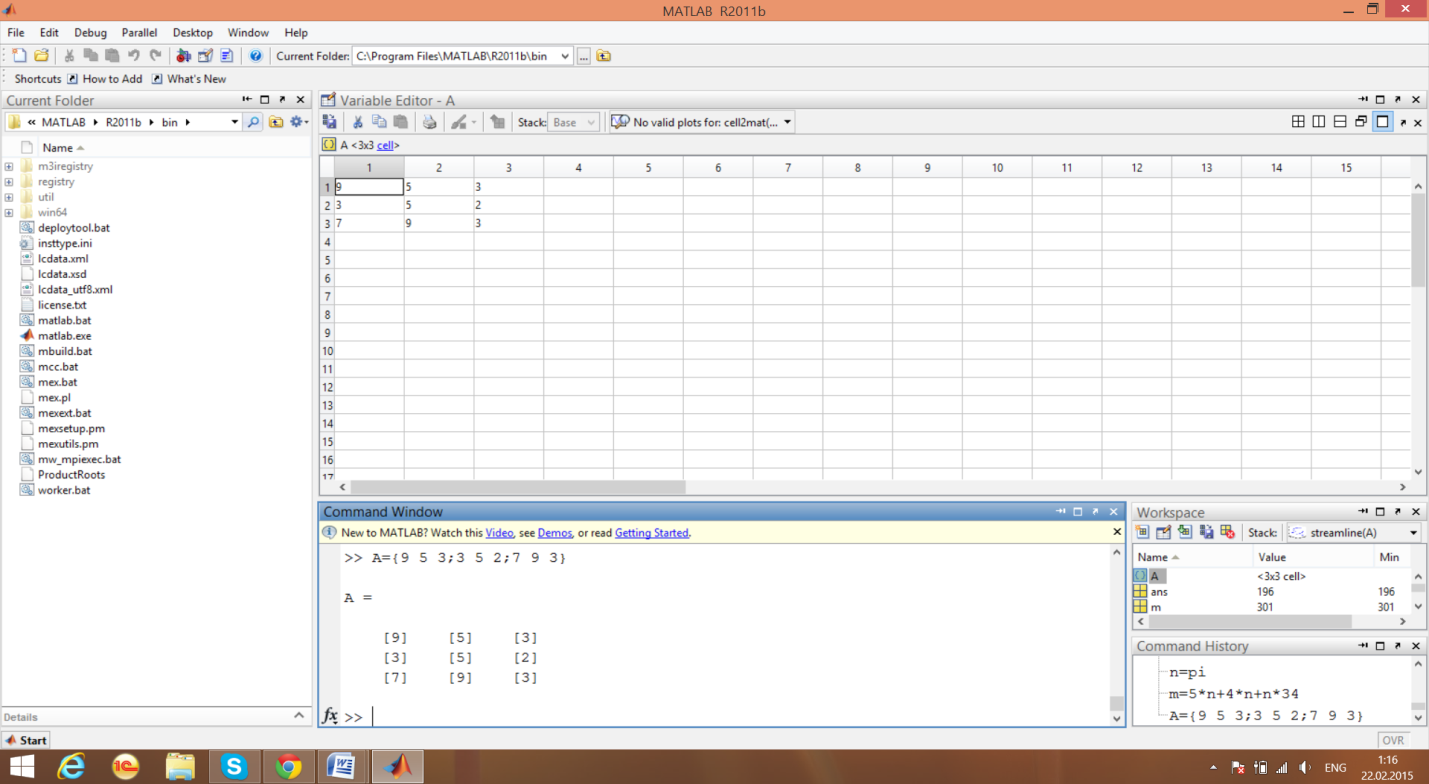
Окно справочной системы MATLAB

комплексные числа

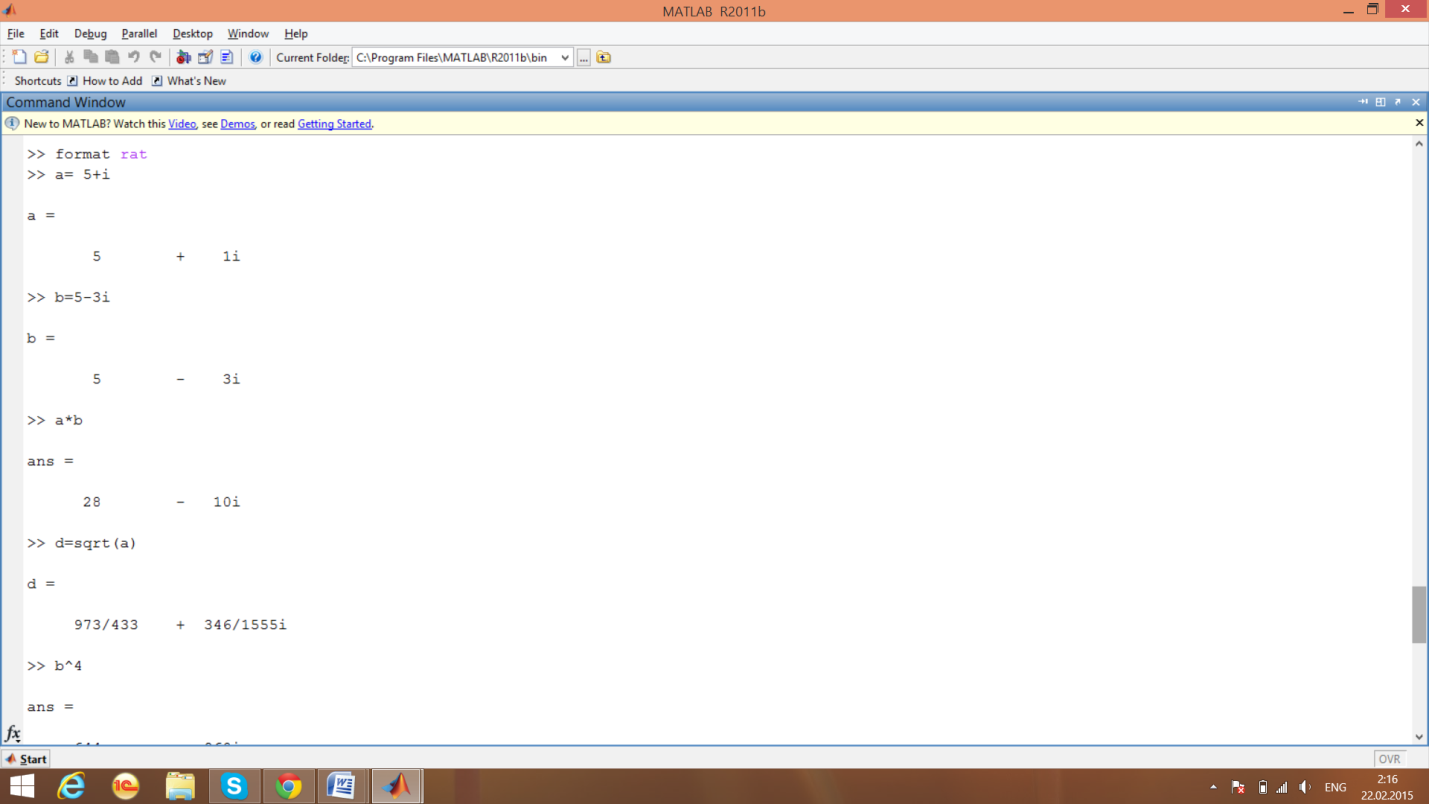
Основные приемы работы с комплексными числами поясним на следую­щих примерах

1)Зададим комплексные числа:

2)Вычислим произведение комплексных чисел

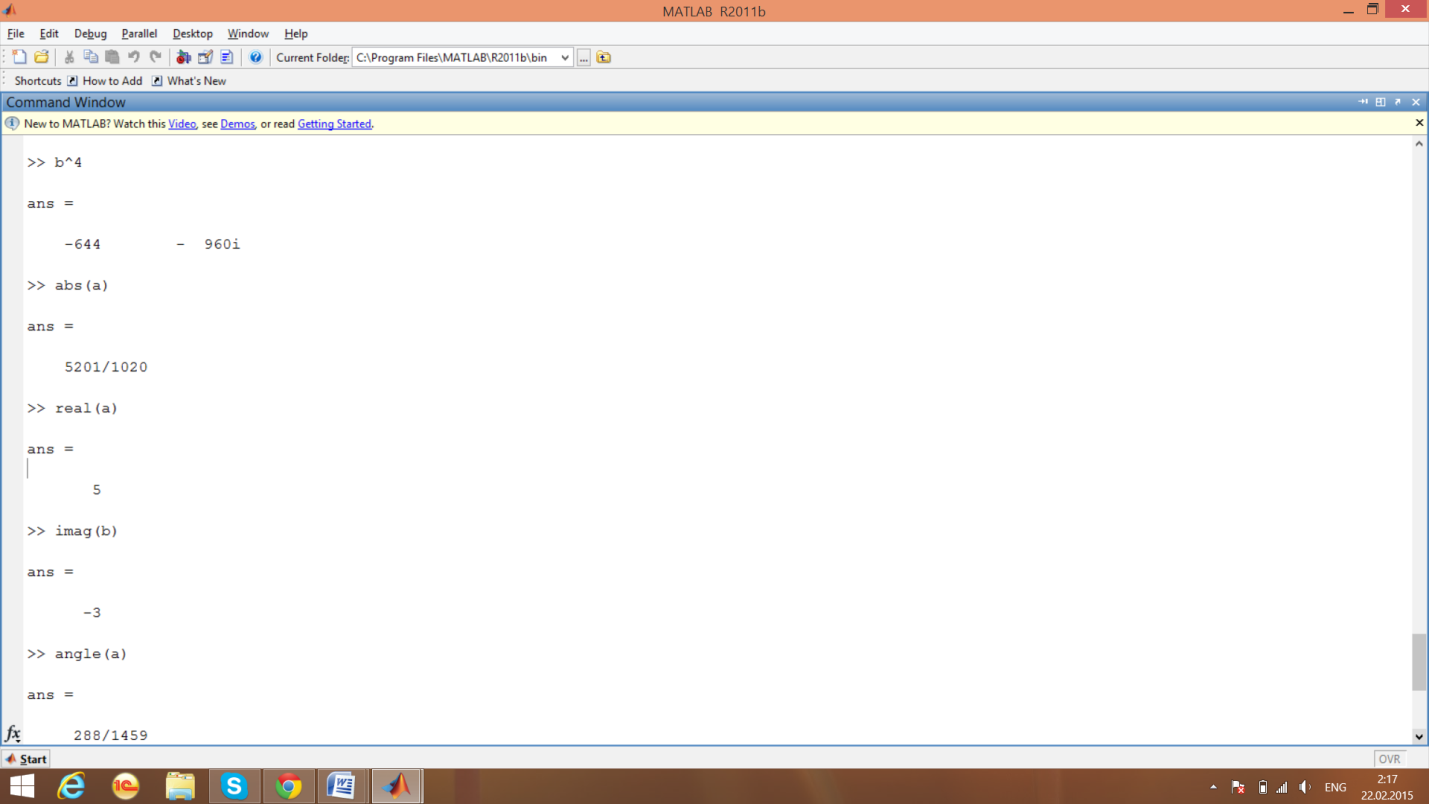
3)Вычислим действительную (re(b)) и мнимую (im(b)) части комплексного числа

4)Вычислим аргумент комплексного числа (arg(a))

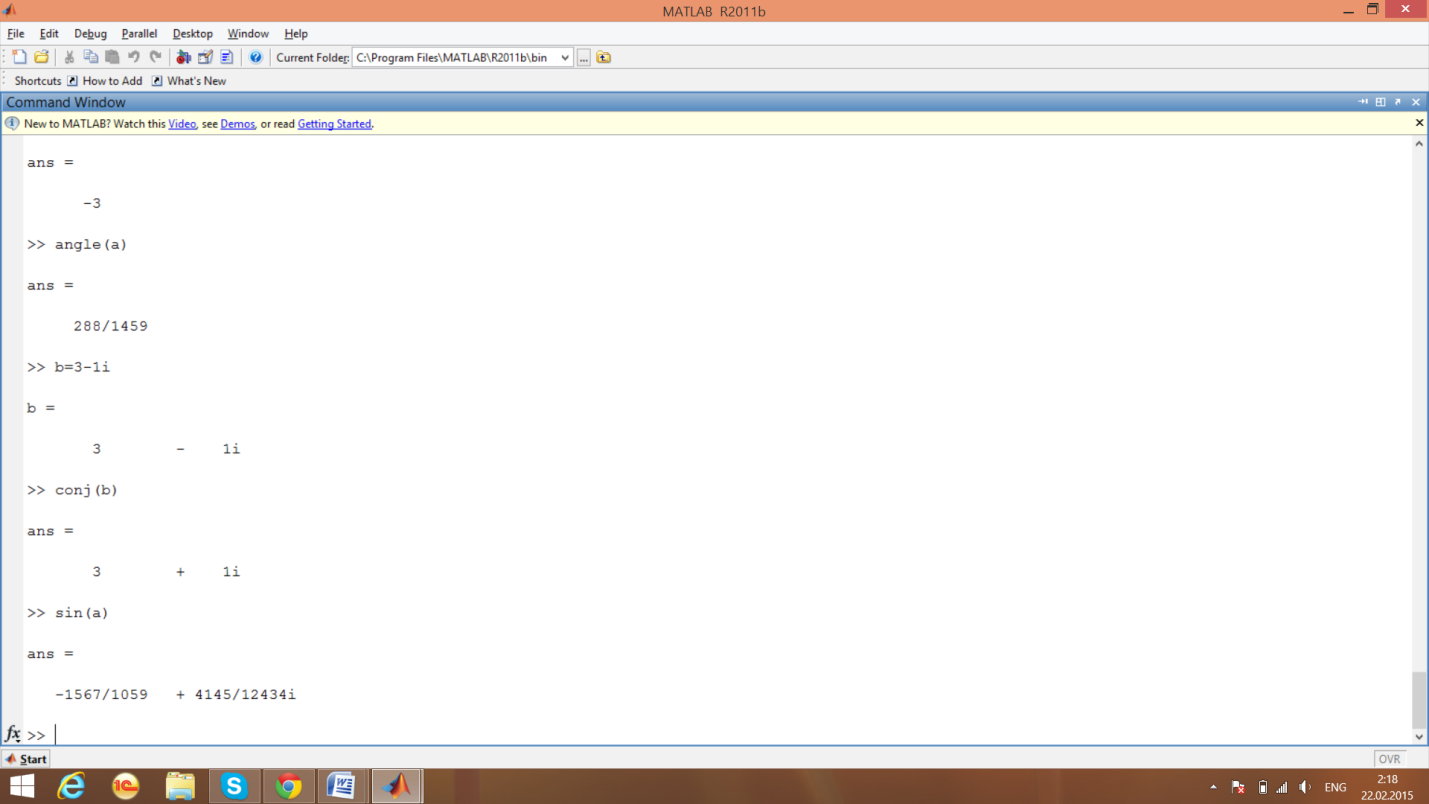
5)вычислим число комплексно сопряженное числу

6)Вычислим sin(a)

векторы и матрицы

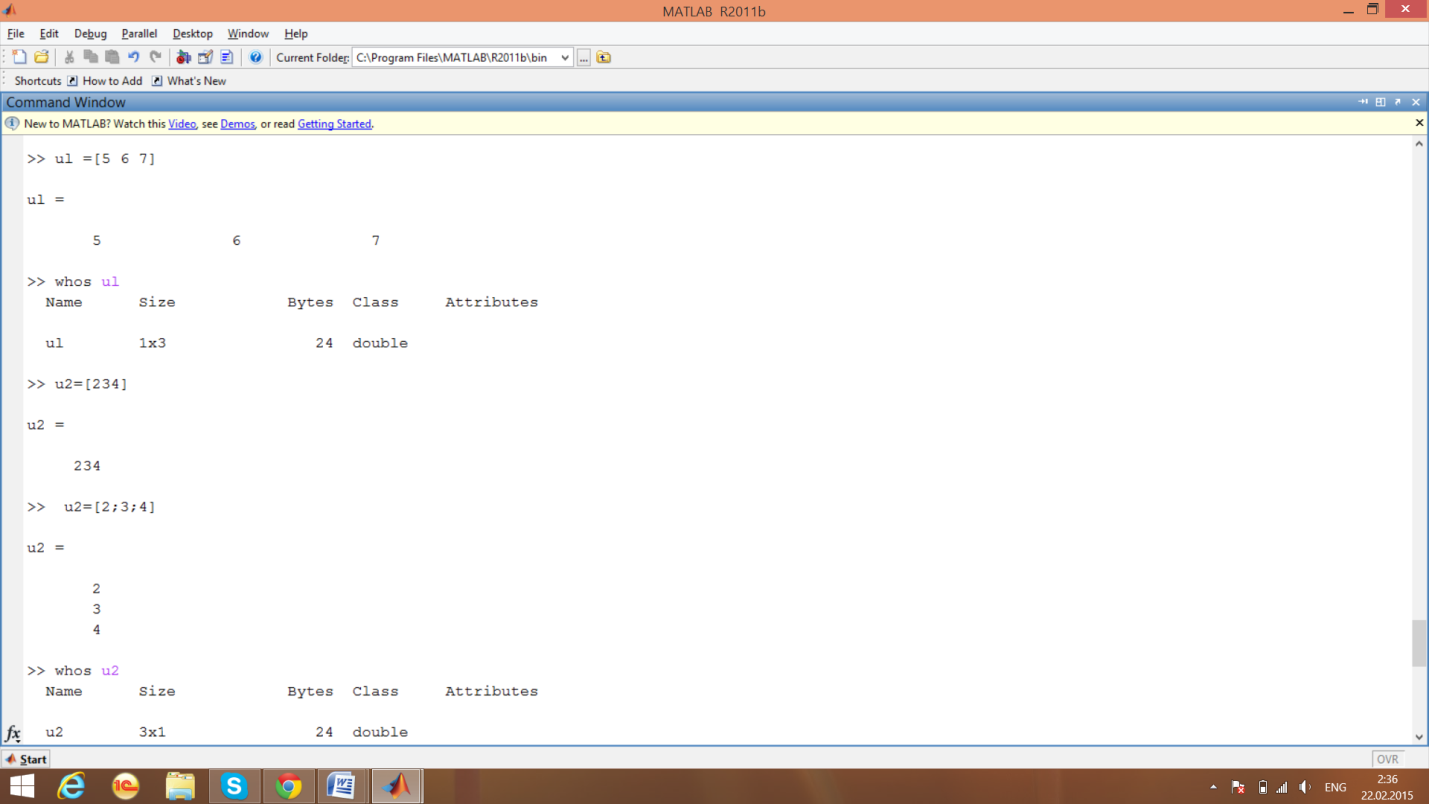
1)Зададим вектор-строку:

2)Зададим вектор-столбец

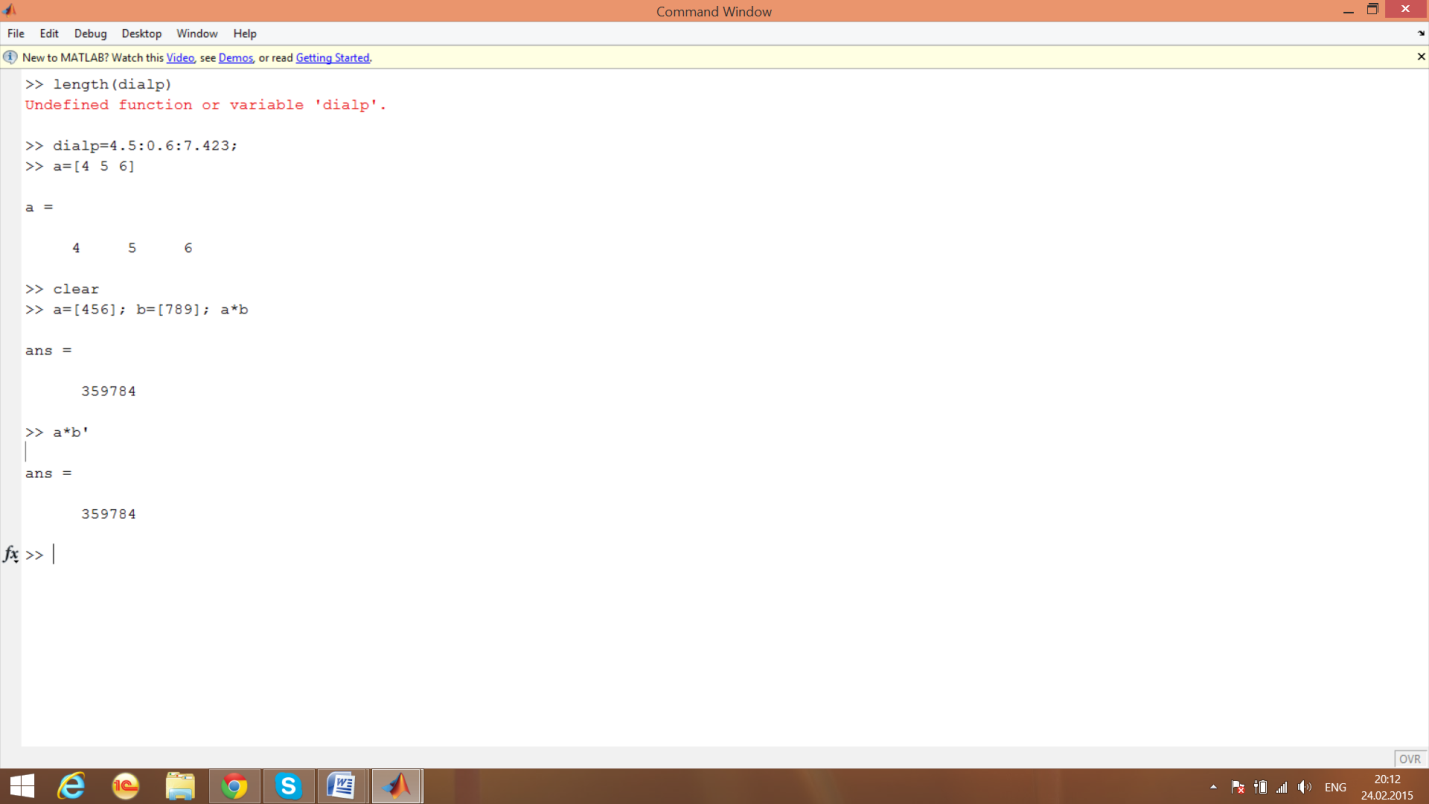
3)Вычислим скалярное произведение векторов

4)Поэлементное умножение векторов

5)Создадим матрицу

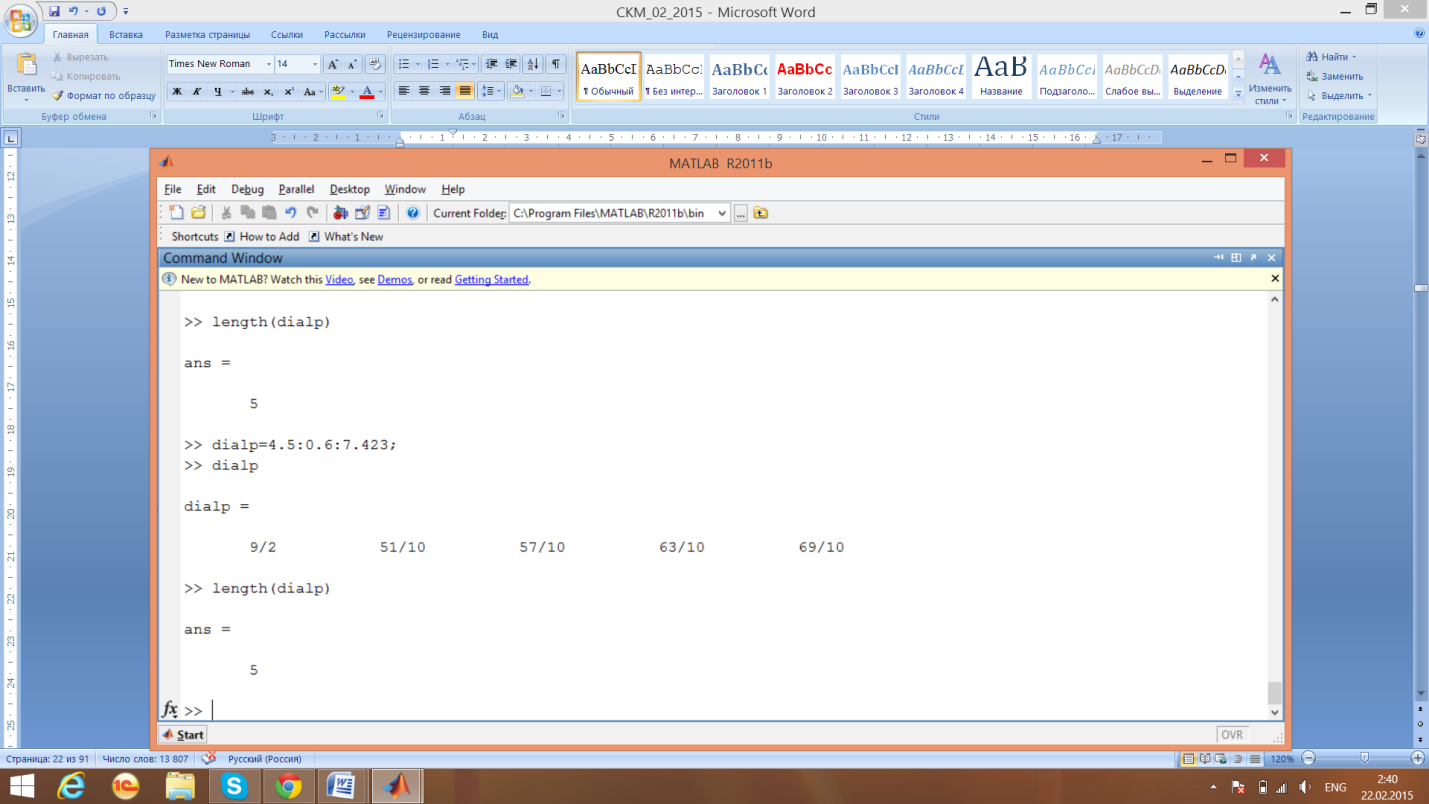
Вычислим скалярное произведение векторов

6. Создадим матрицу

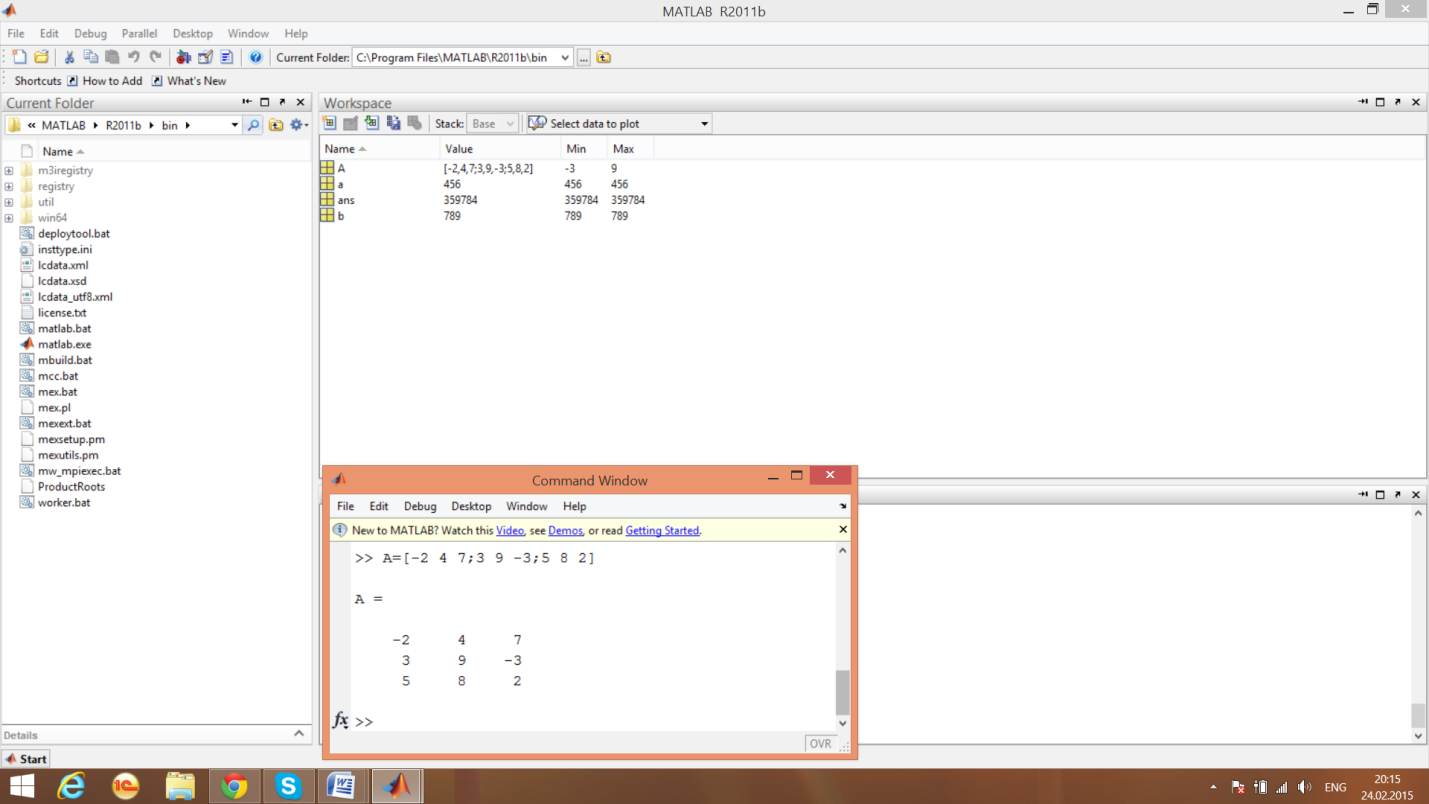
7. Выделим заданный столбец матрицы

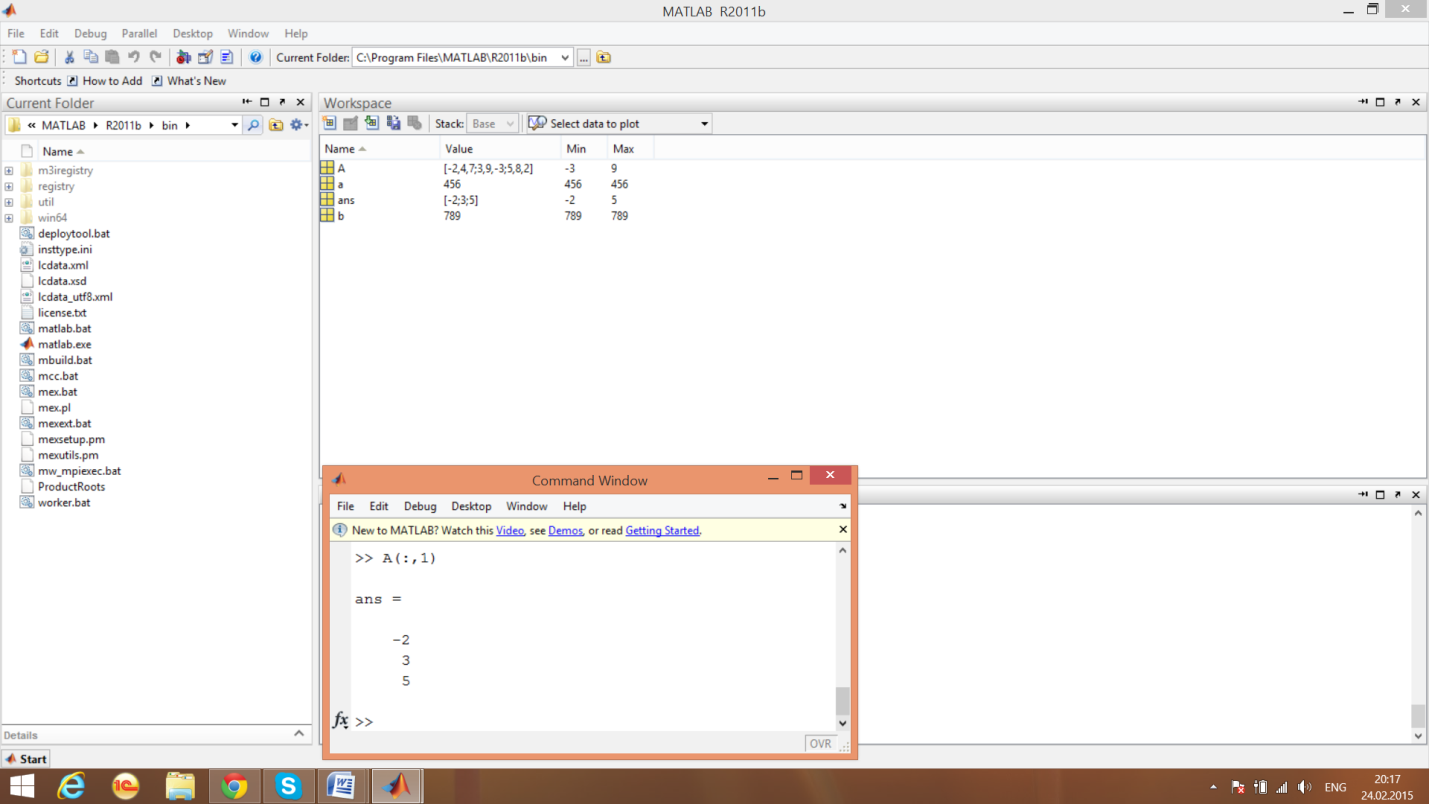
. Выделим заданную строку матрицы

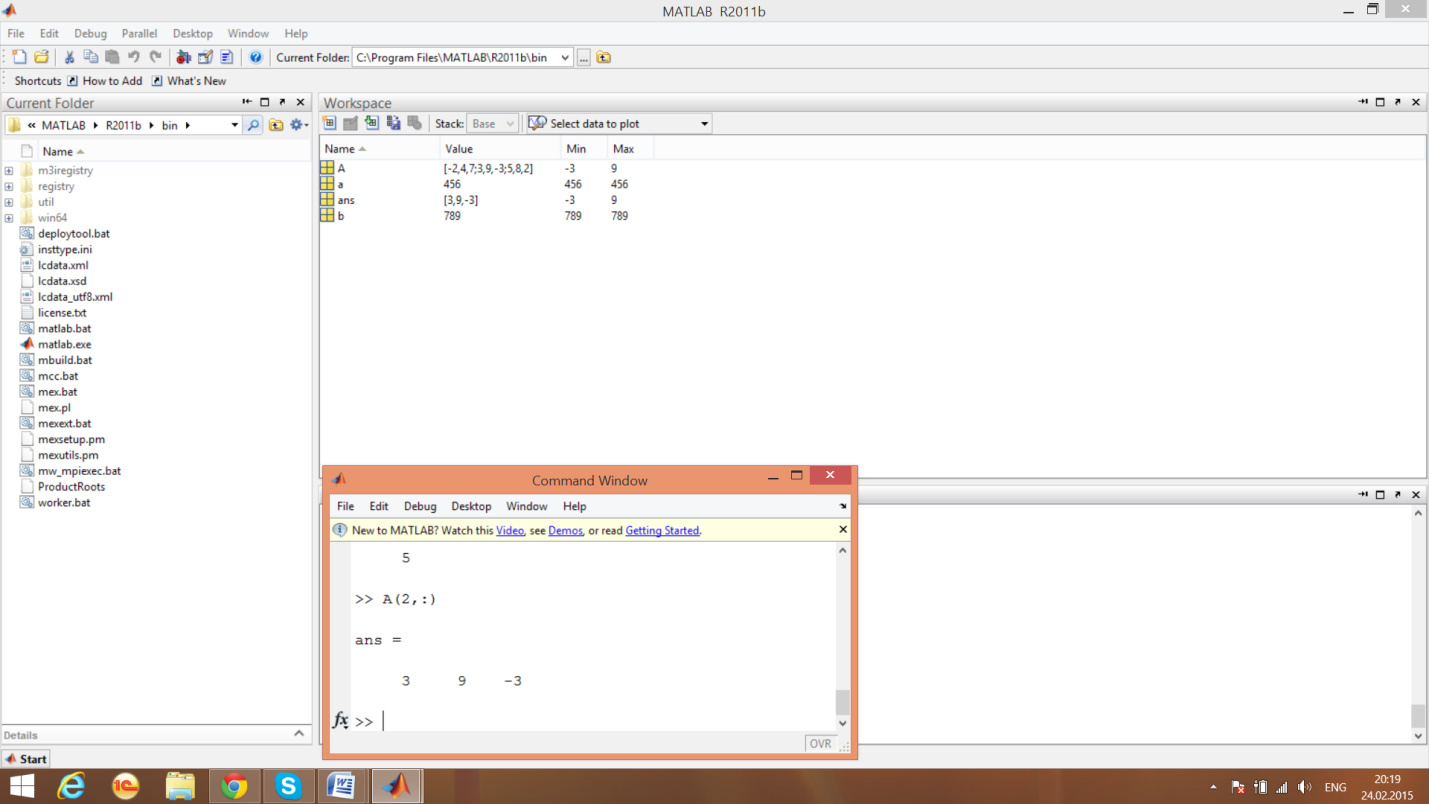
Выделим определитель матрицы

Вычислим обратную матрицу

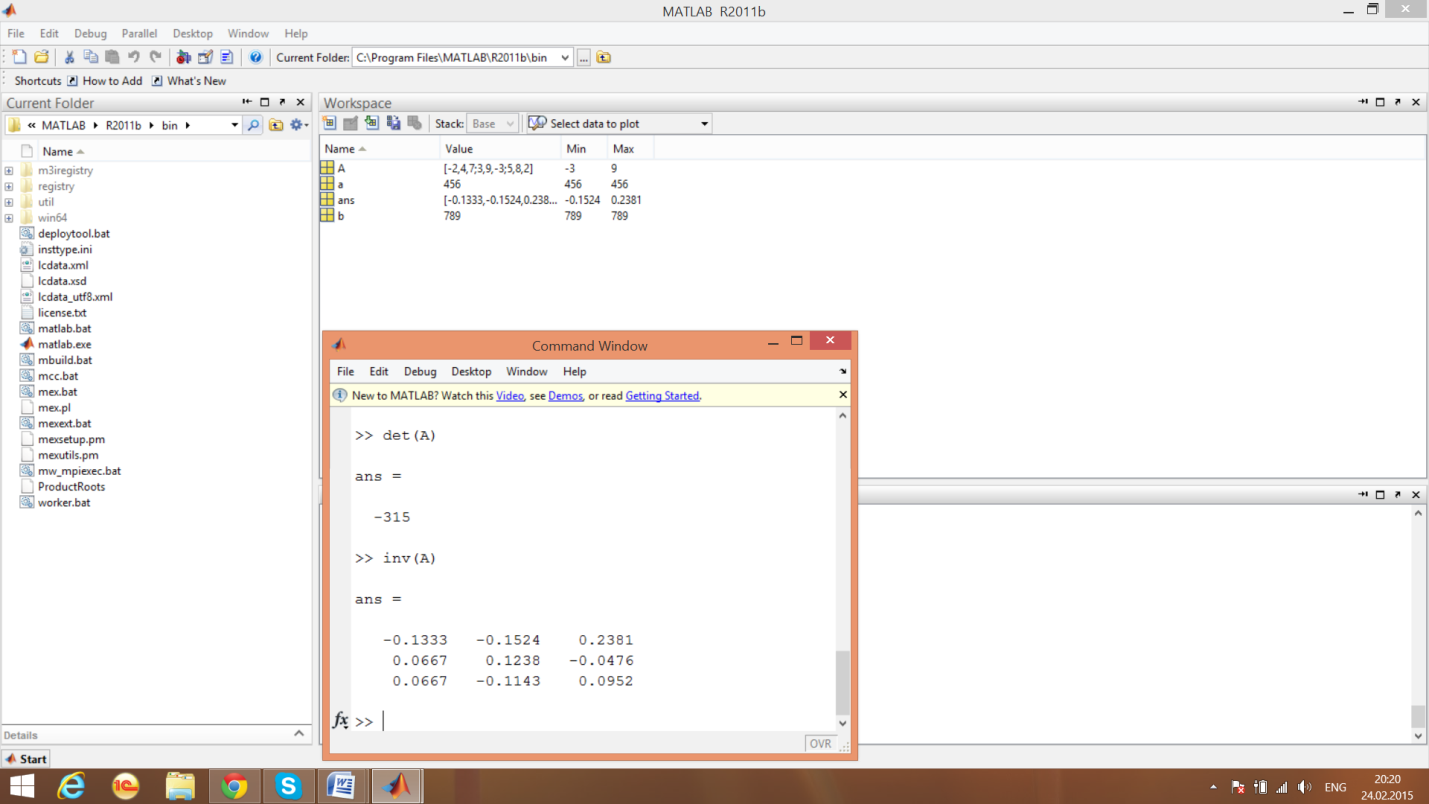
Элементарные функции

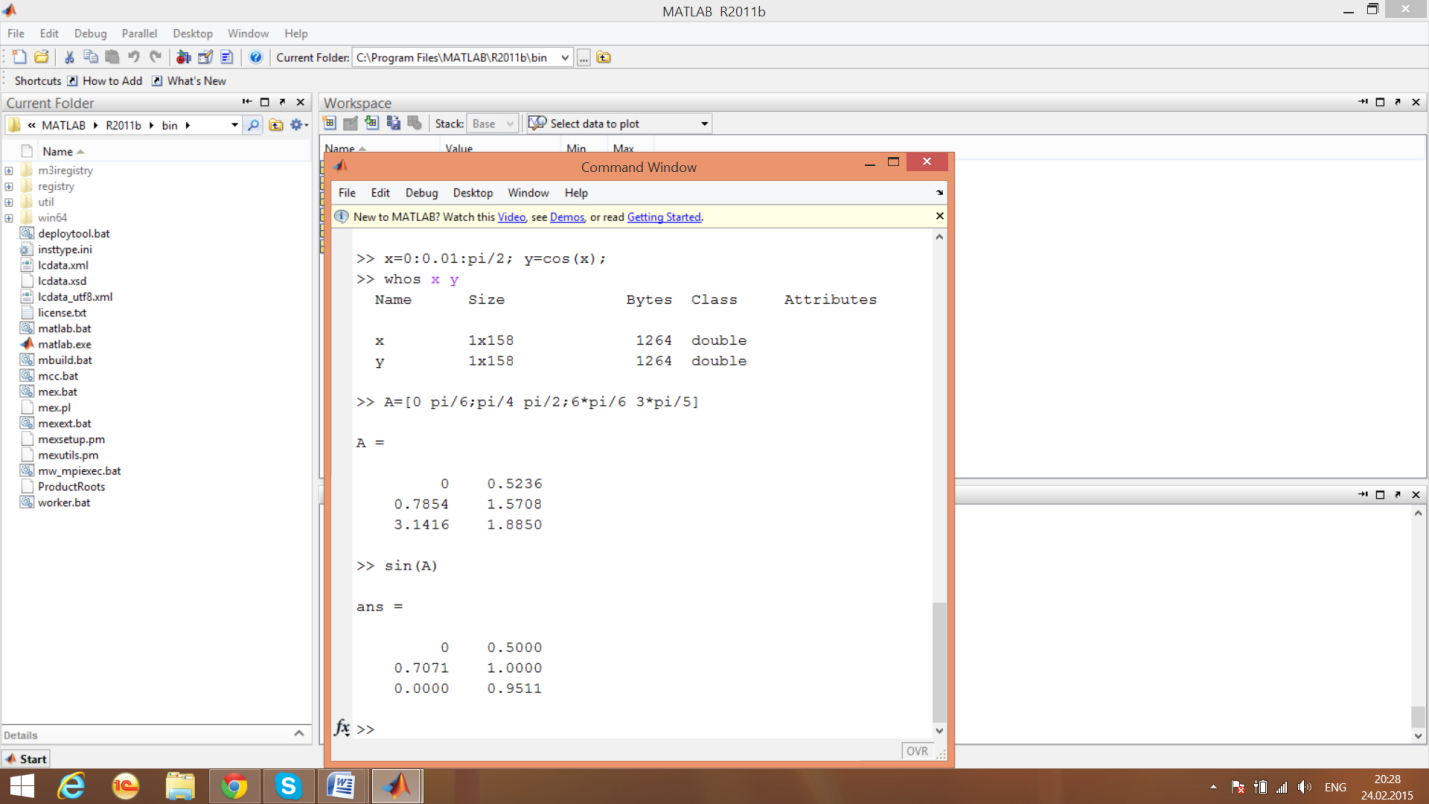Функции MATLAB для создания

передаточных функций звеньев системы

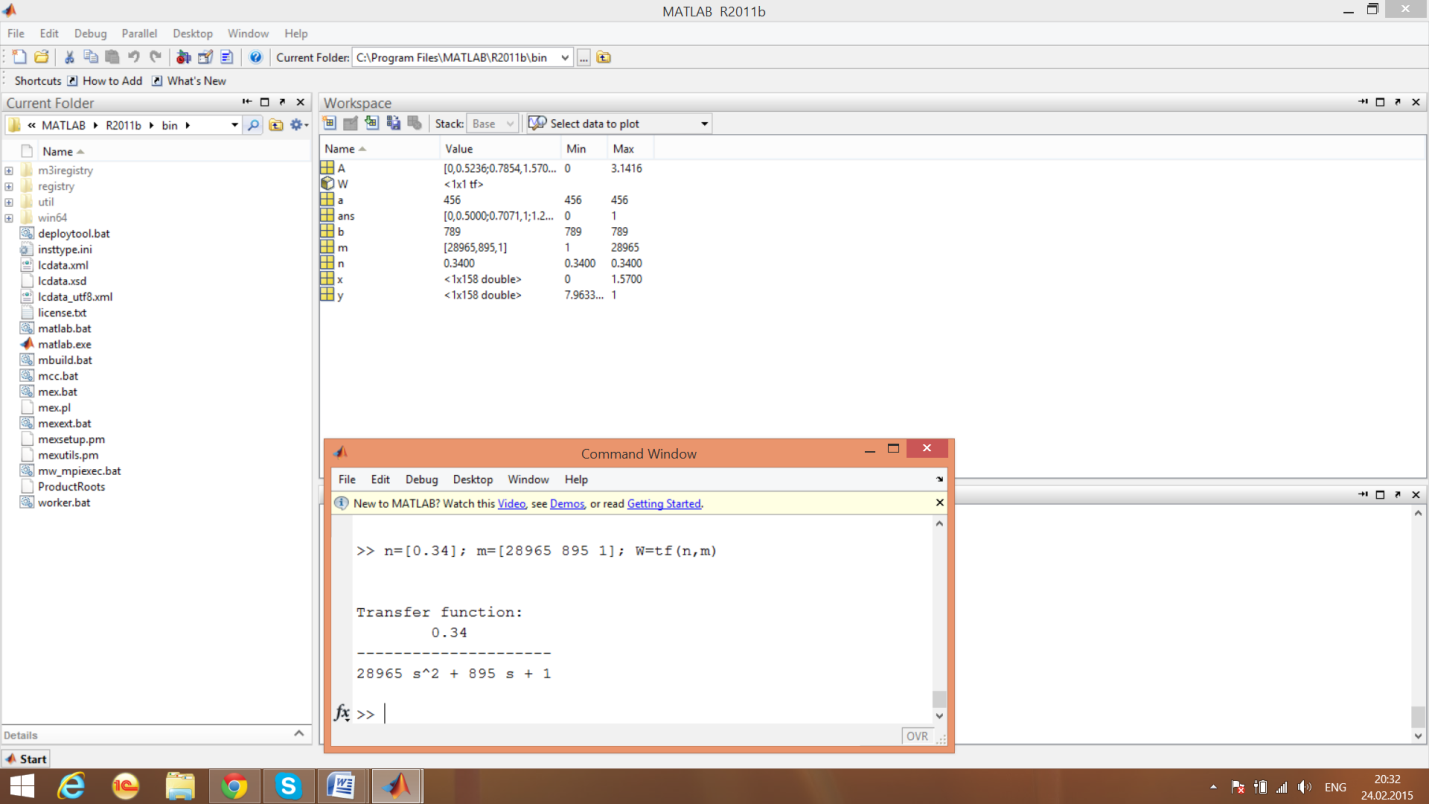
Образование передаточной функции

Функции pole() и zero()

Функции предназначены для определения, соответственно, по­люсов и нулей передаточной функции G(S).

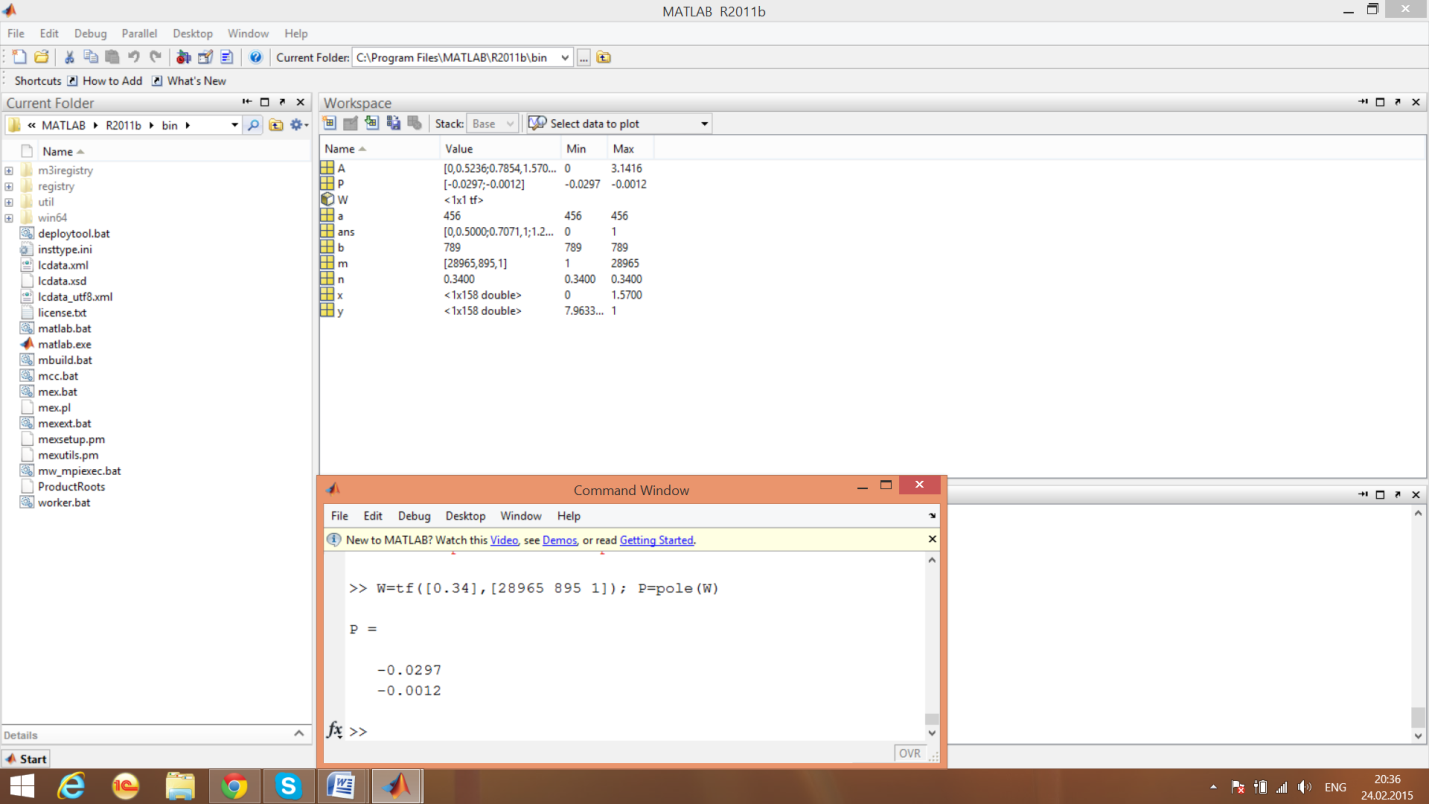
Определение нулей и полюсов передаточной функции

Функции roots() и poly()

Функции предназначены, соответственно, для вычисления корней полинома и его восстановления по значениям корней

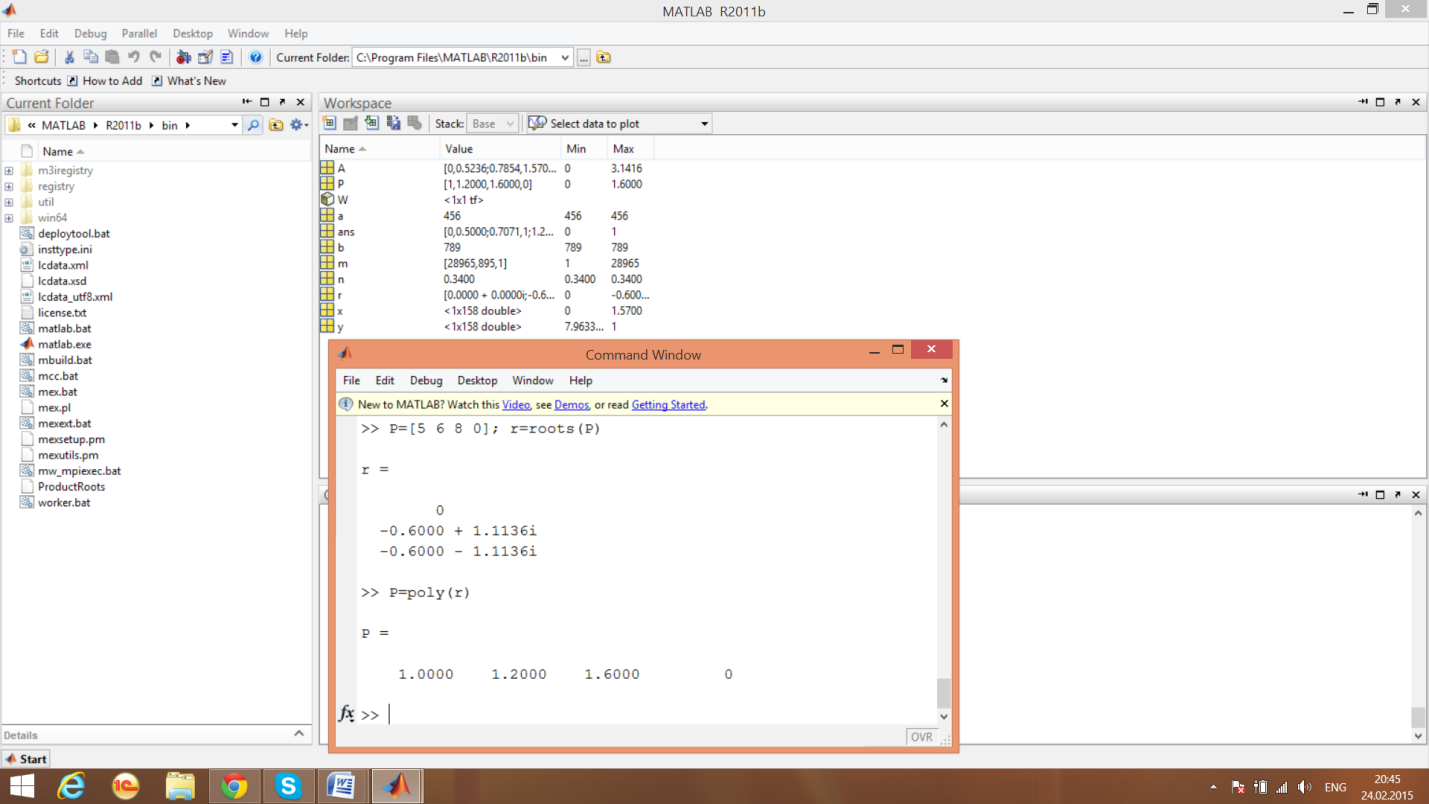
Функции определения корней полинома и его восстановления

Функция conv()

Функция применяется для умножения полиномов p(s) и q (s).

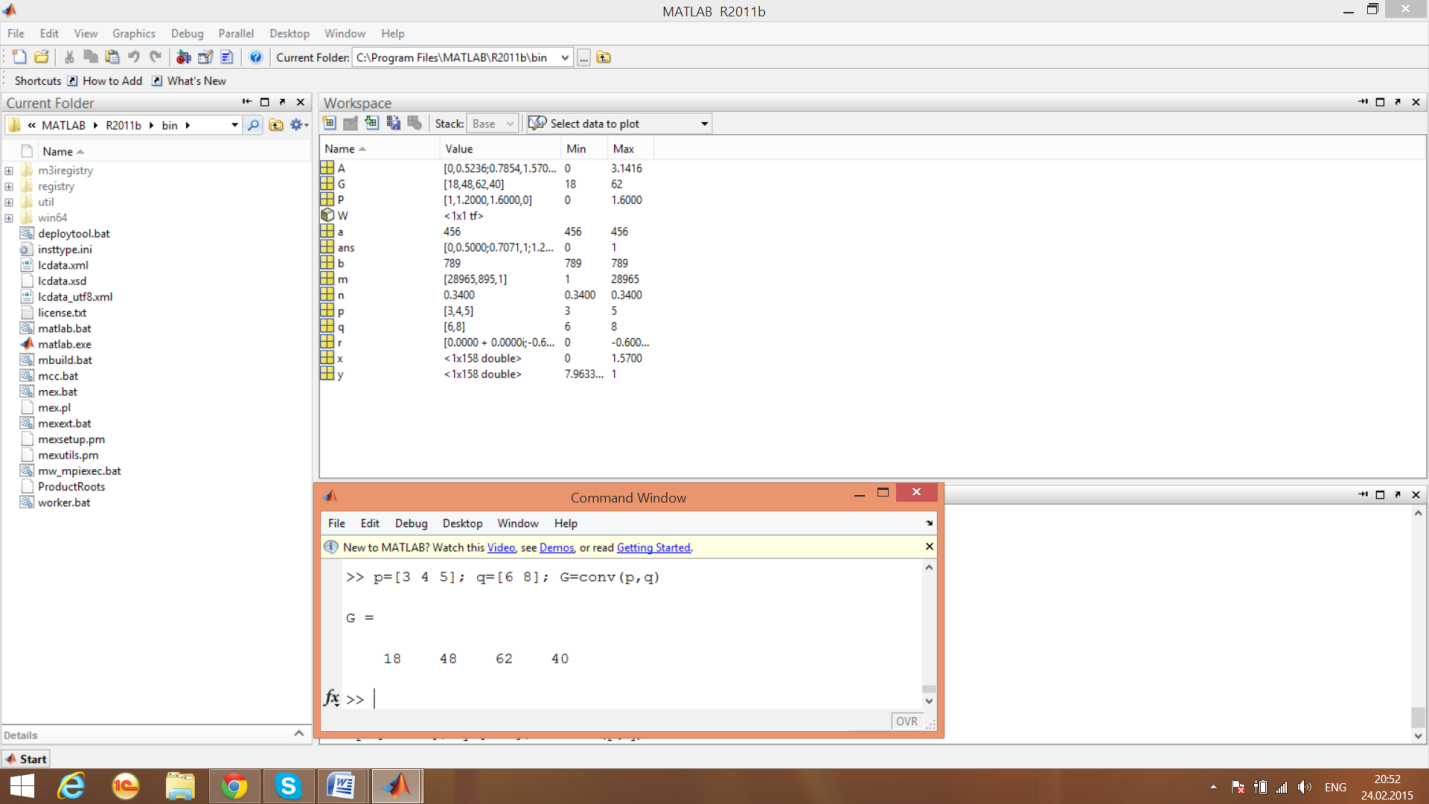
Процедуры умножения полиномов

Функция polyval ()Функция предназначена для вычисления значений полинома при заданном значении переменной

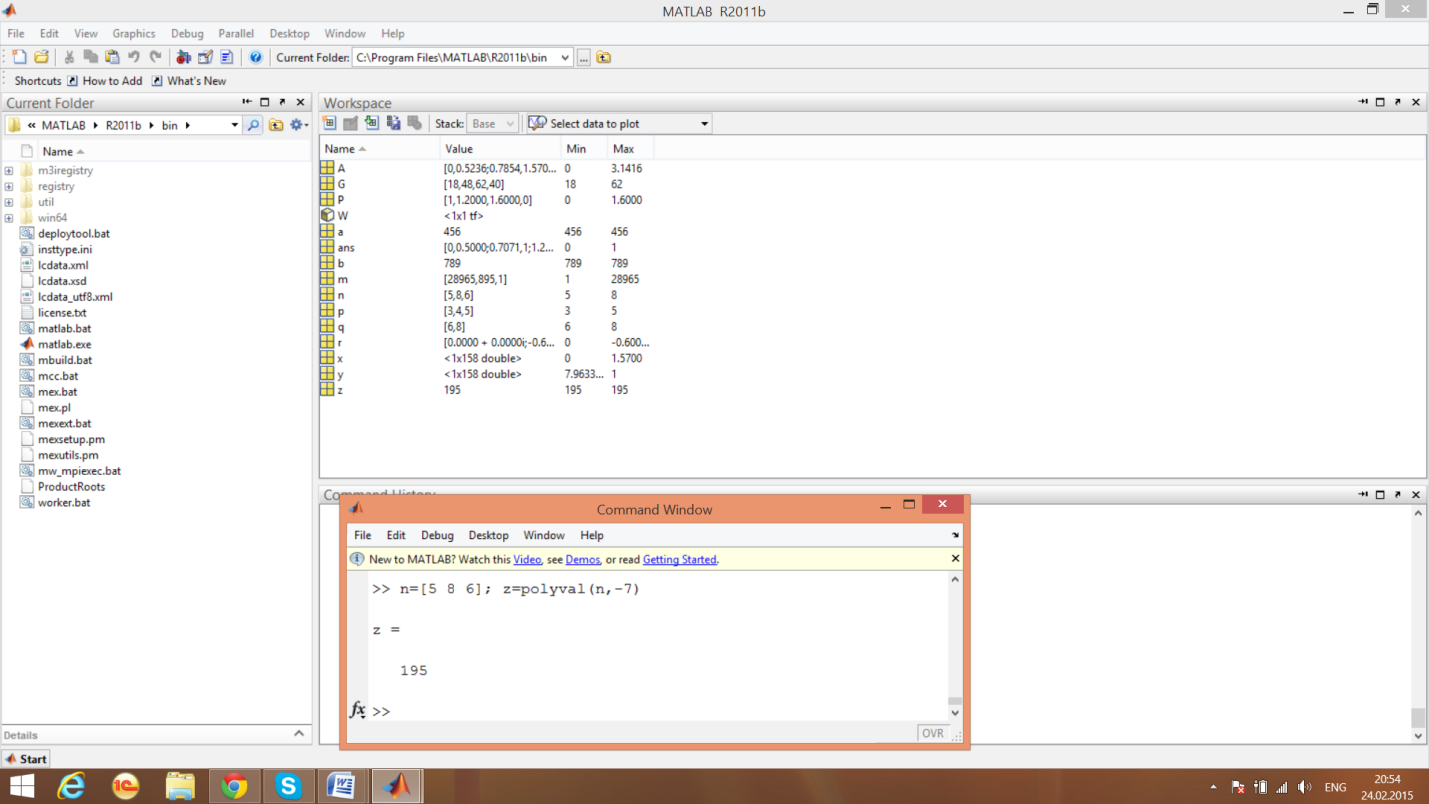
. Вычисление значений полинома

1.3. Операции с передаточными функциями звеньев

1.3.1. Сложение передаточных функций

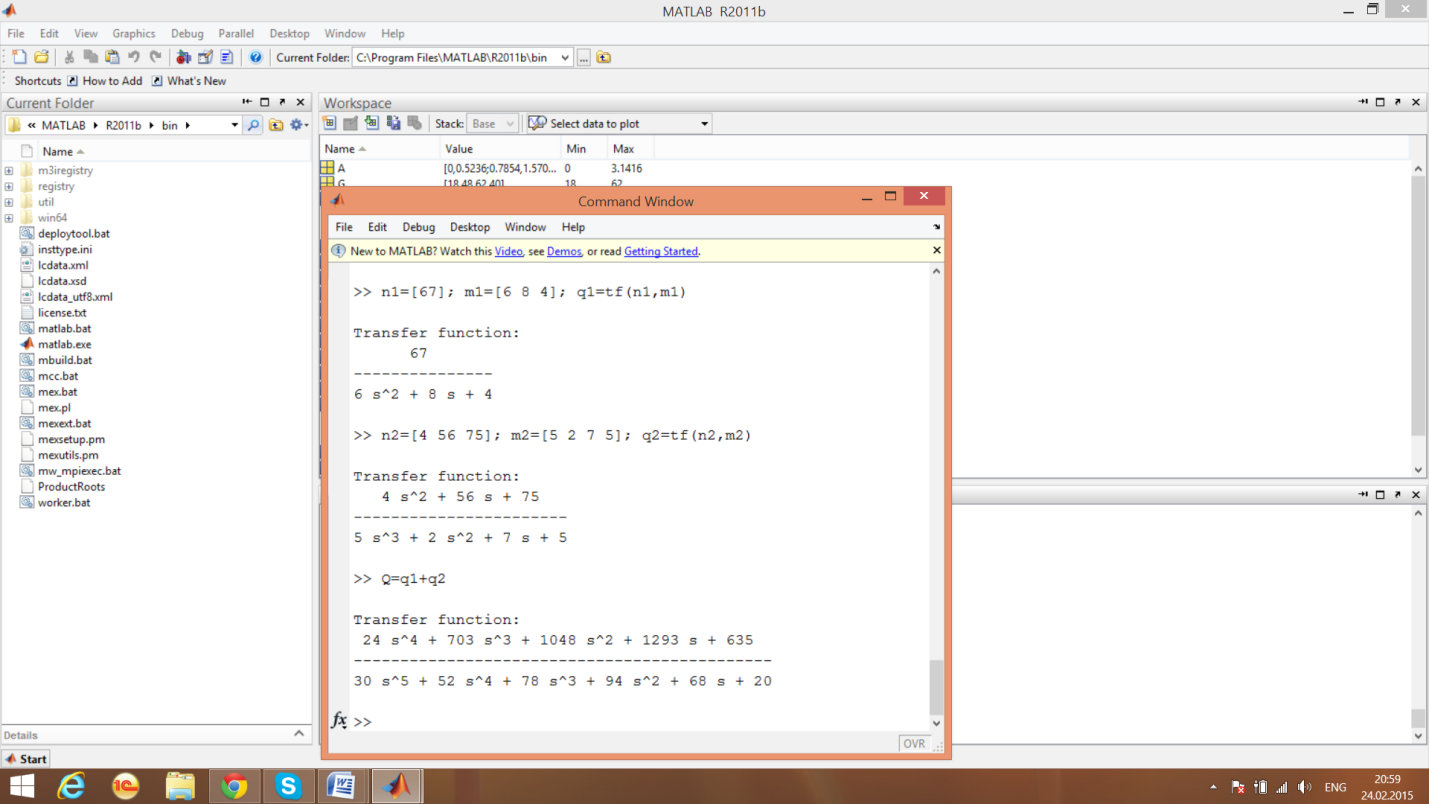
операции вычитания, умножения и сложения передаточных функций с помощью операторов –, *, /.

Функция pz map ()

Функция pzmap() показывает расположение полюсов и нулей передаточной функции на комплексной плоскости S.

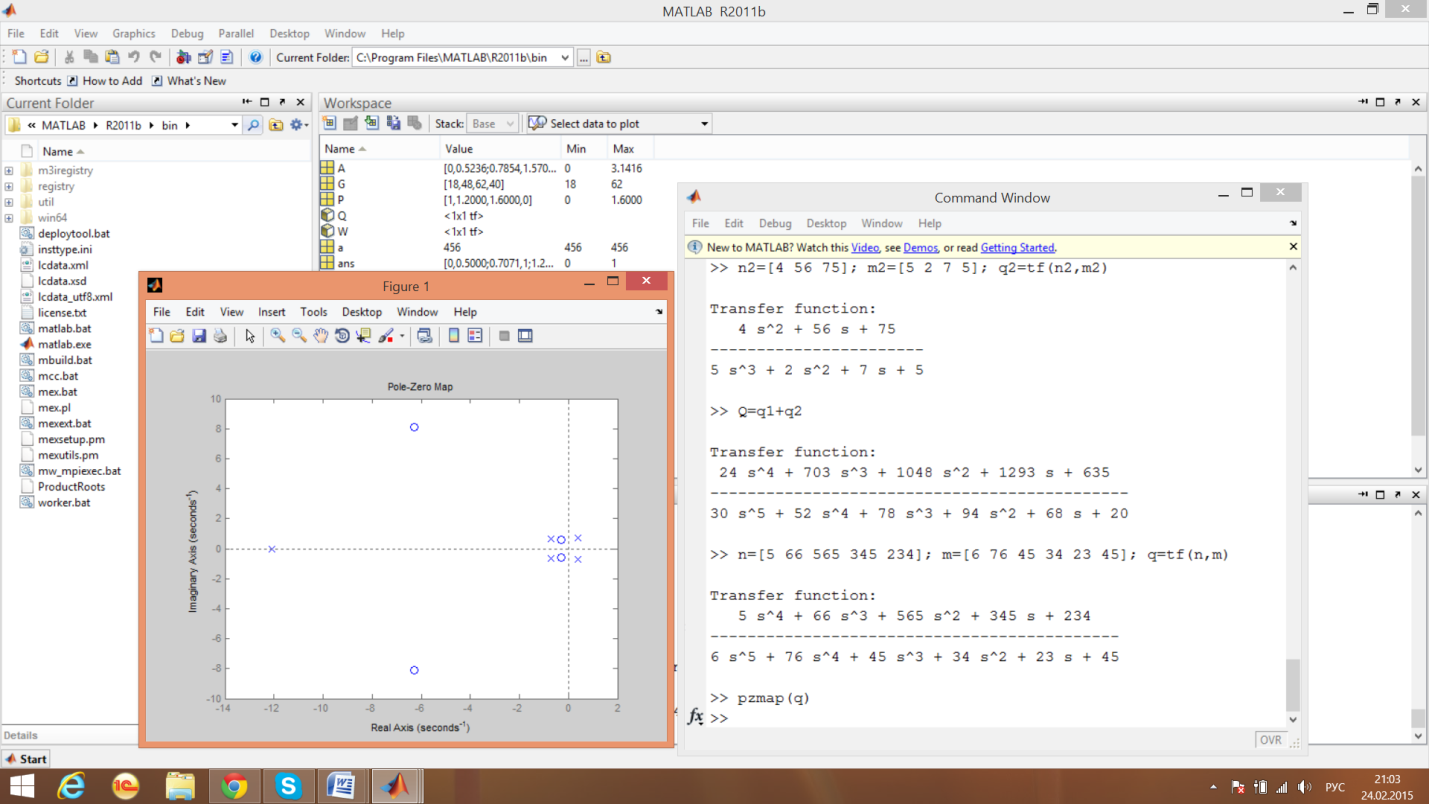Определение нулей и полюсов передаточной функции

Нули и полюсы передаточной функции

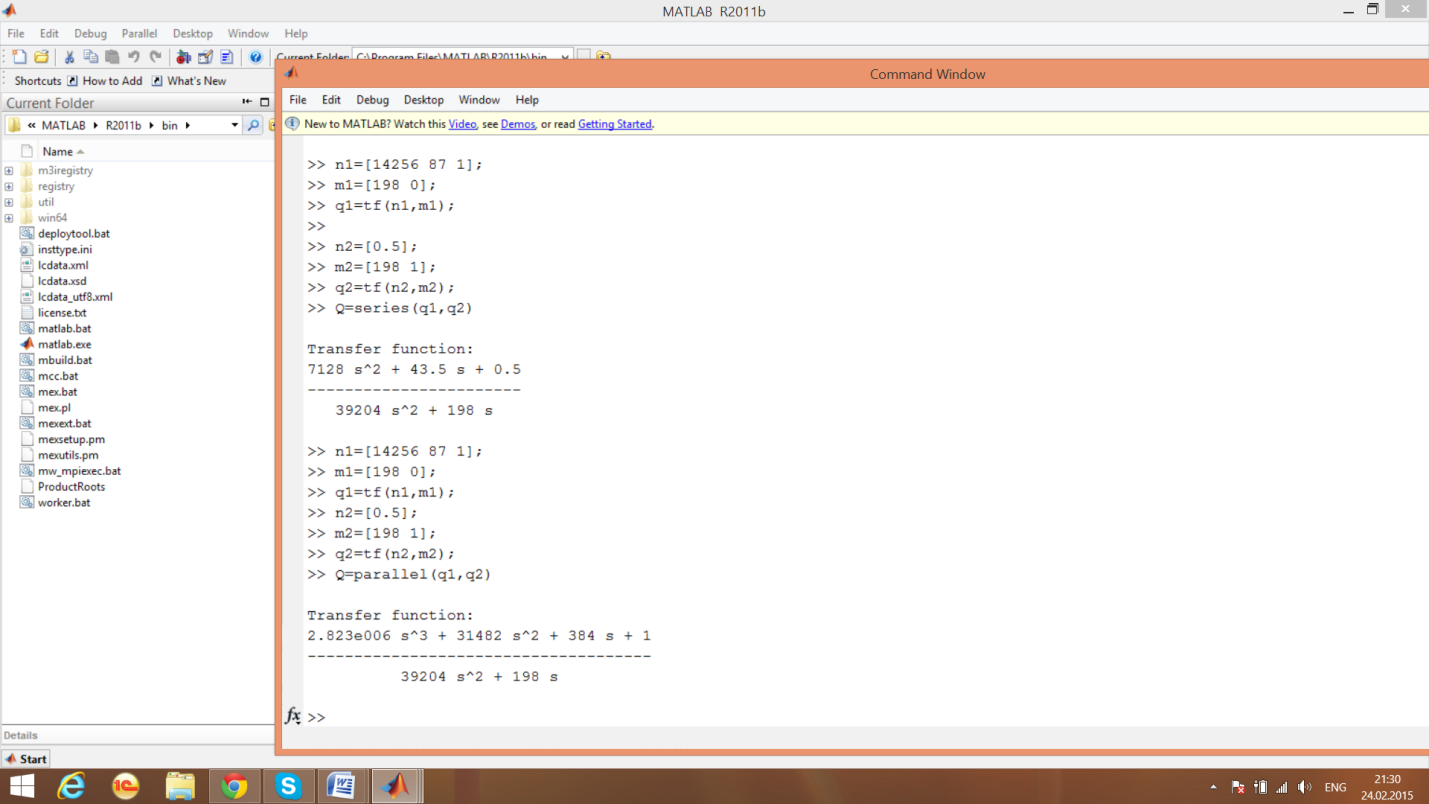
Функция series ()

Структурная схема системы управления

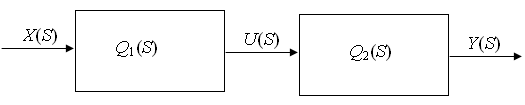
Функция parallel ()

Структурная схема системы,состоящая из параллельных звеньев

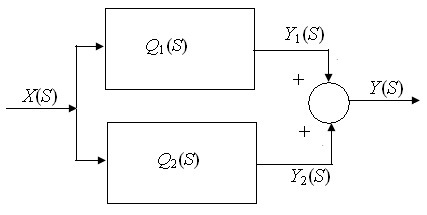
Функция feedback ()

Структурная схема системы управления

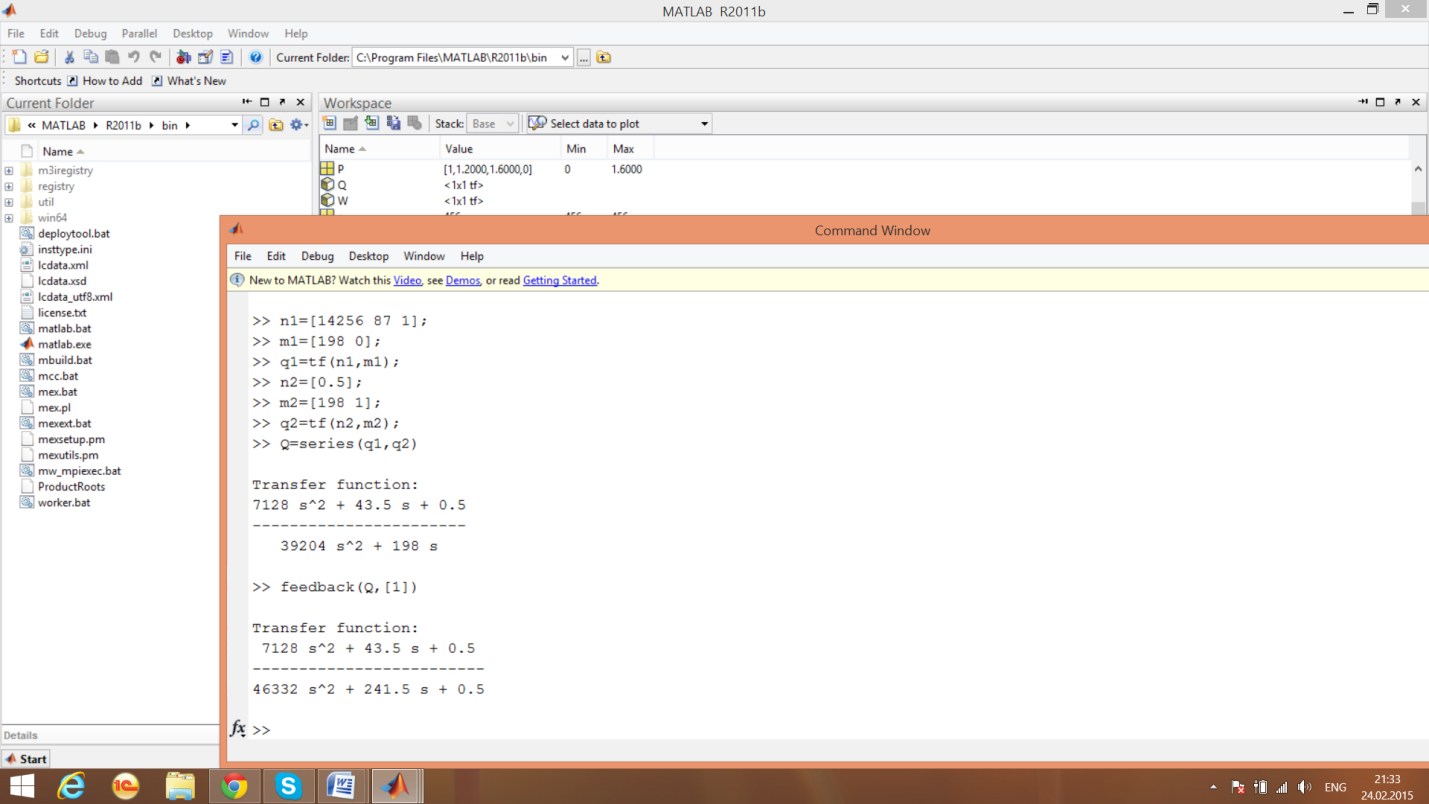
Образование передаточной функции системы

с жесткой отрицательной обратной связью

Структурная схема системы

с гибкой отрицательной обратной связью

Передаточные функции звеньев имеют вид

Пропускаю часть 3.1

Сложение комплексных чиcел

Пример 1

Z1=1+4i, Z2= 4-6i;

Z1+Z2=1+4i+4-6i=5-2i;

Вычитание комплексных чисел

Пример 2

Z1=1+4i, z2=4-6i;

Z1-z2= 1+4i-4-6i=-3-2i;

Умножение комплексных чисел

Пример 3

Z1=1-i, z2= 2+6i;

Z1*z2=

Построим на комплексной плоскости следующие комплексные числа

Z1=1,Z2=-2 , , , , , ,

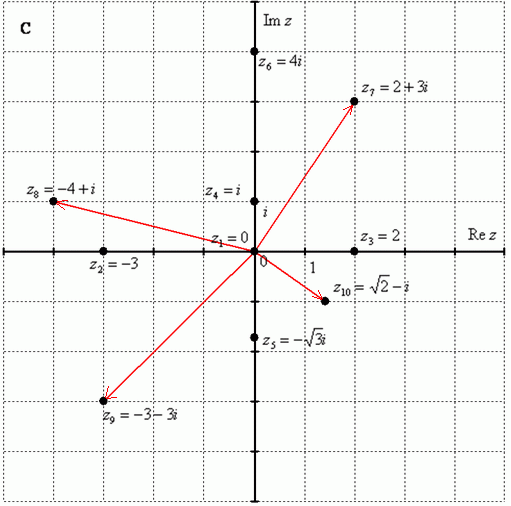
Изобразим на комплексной плоскости число . Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что :

Представить в тригонометрической форме комплексные числа: , , , . Выполним чертёж:

Представить в тригонометрической форме комплексные числа: , , , .

3.2. Операции с числами

3.2.1. Ввод действительных чисел

Рис. 3.1. Командное окно

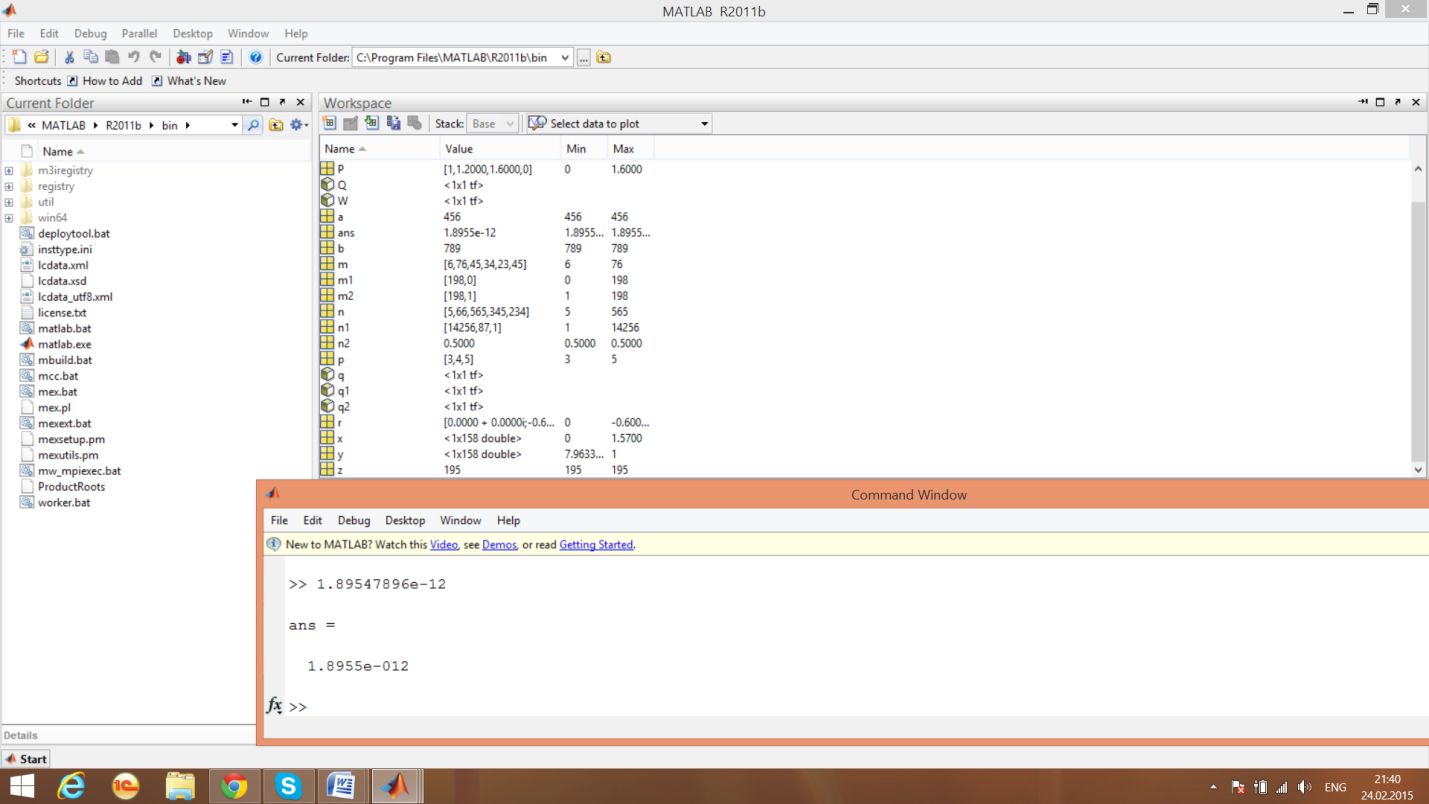
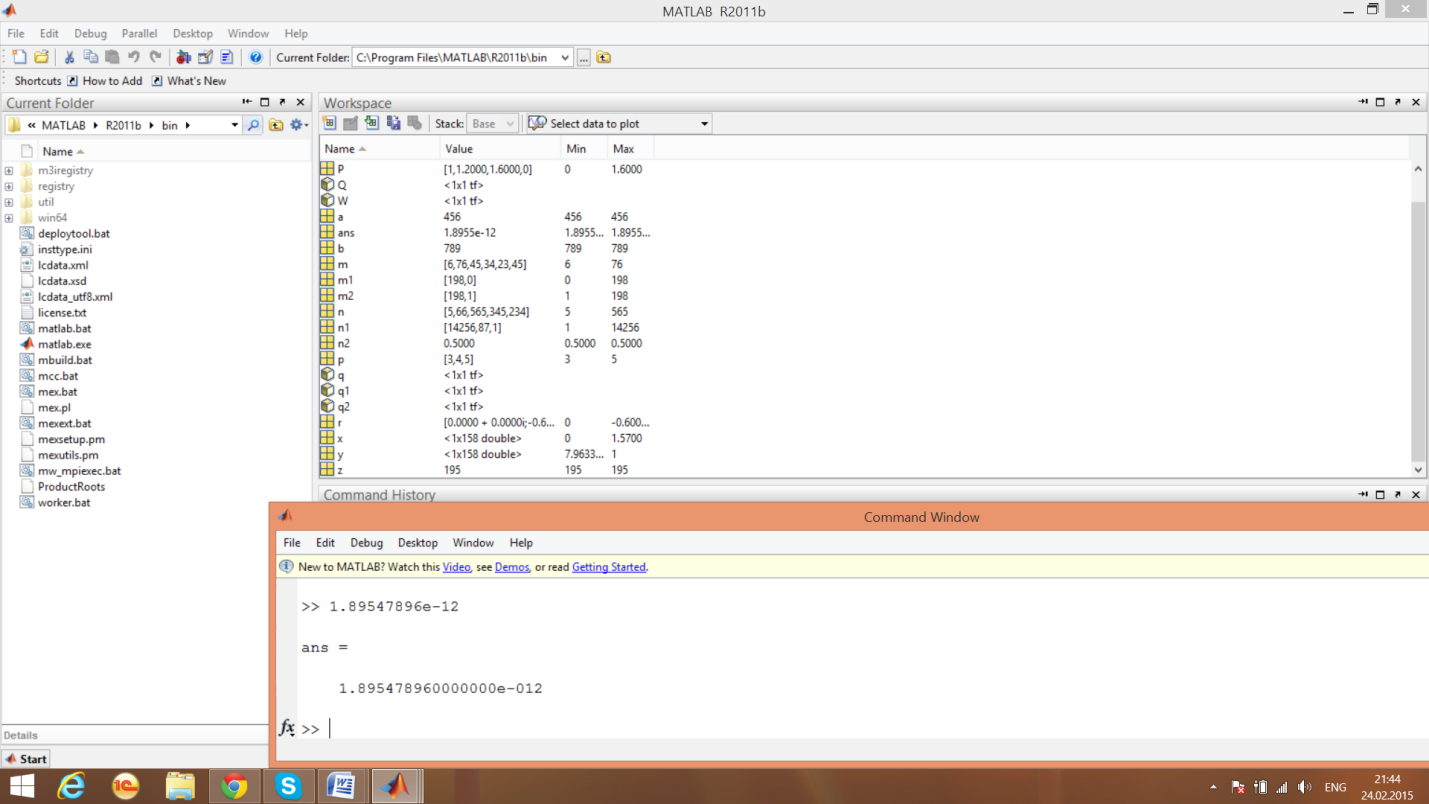. Ввод комплексных чисел

Обозначение мнимой части

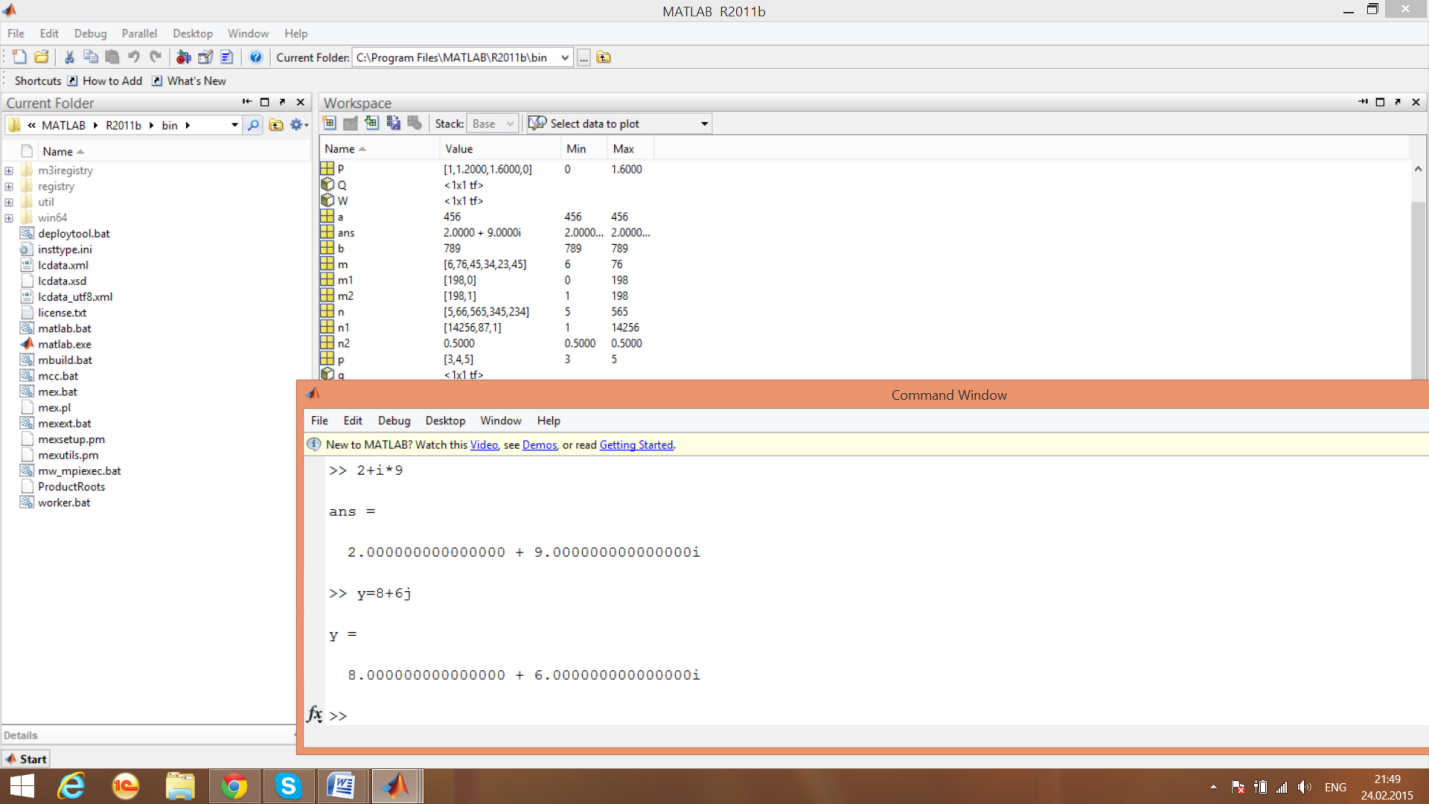Элементарные математические функции

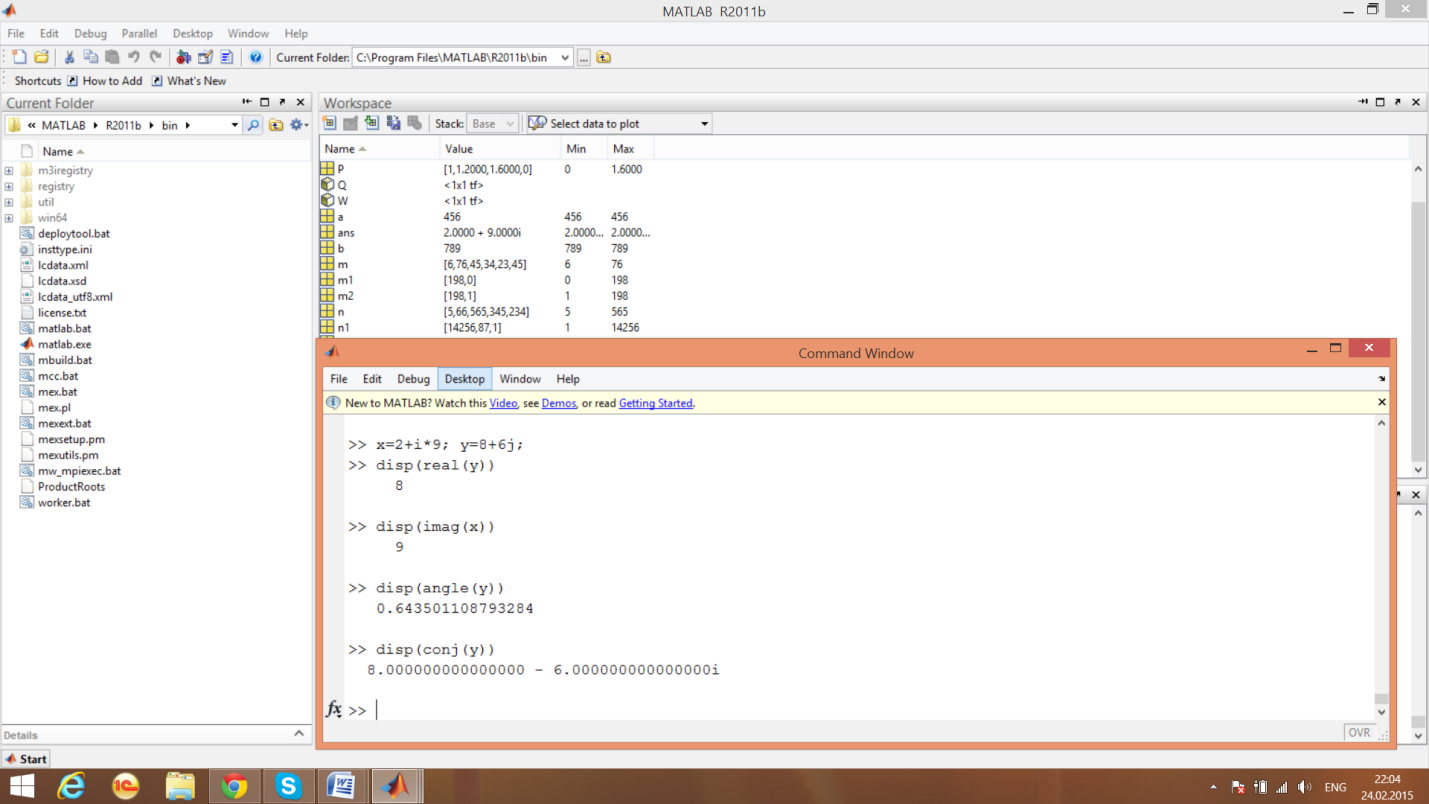
3.2.5. Элементарные действия с комплексными числами

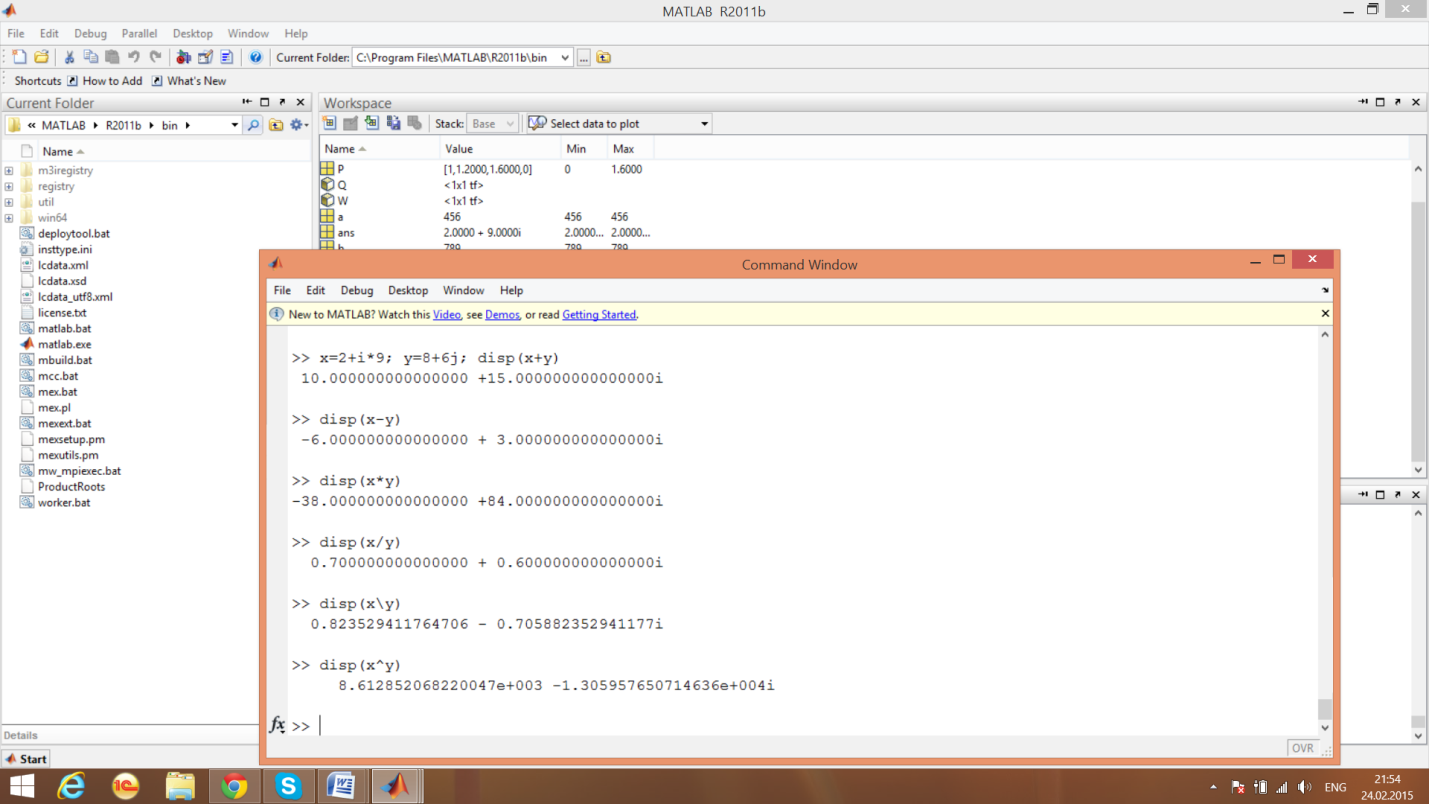
Функции комплексного аргумента

Комплексные числа от элементарных функций

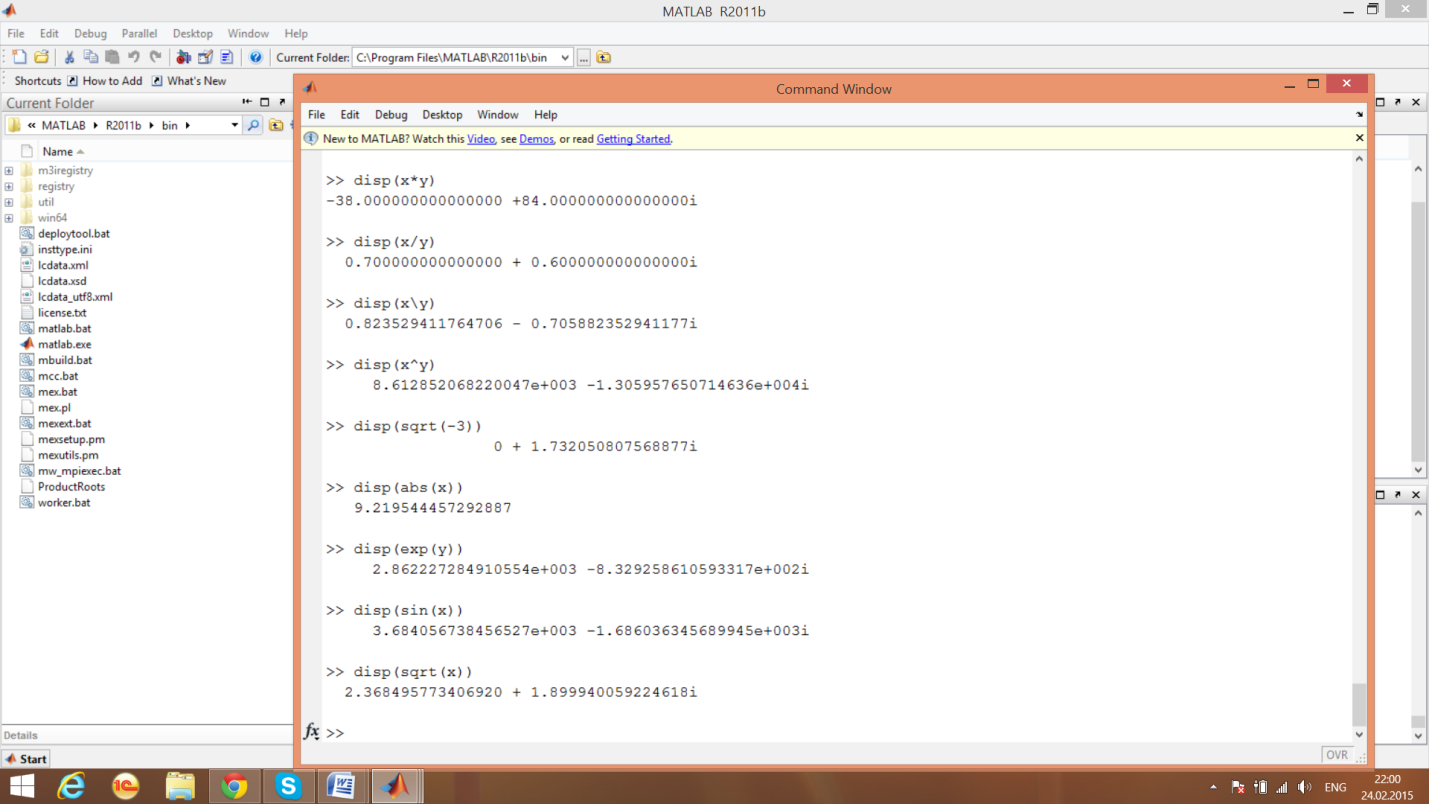
Комплексные числа от дополнительных функций

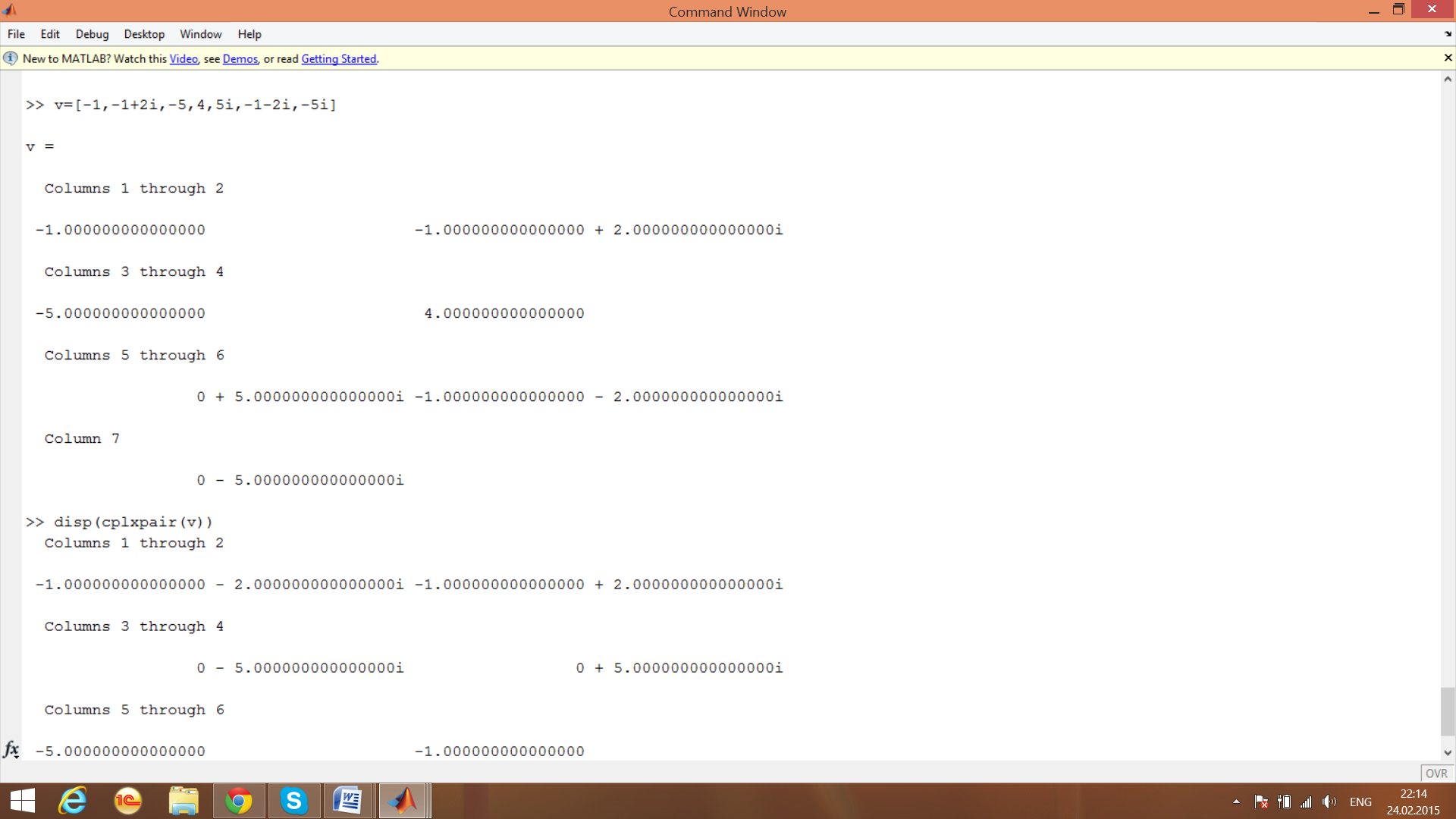
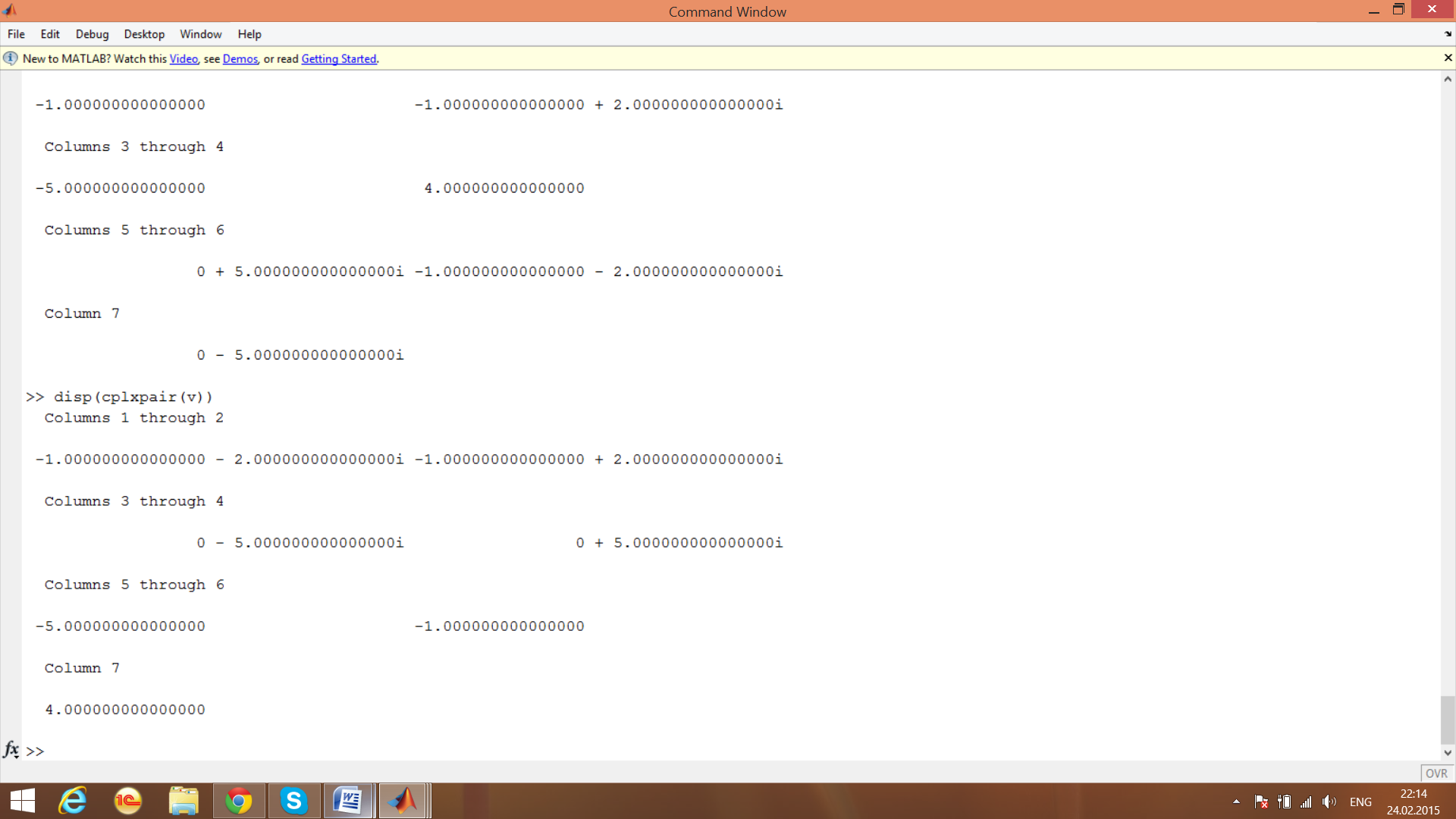
пропускаю 14 примеров

4. Алгебра вектор и матриц

4.1. Создание векторов и матриц

пример1

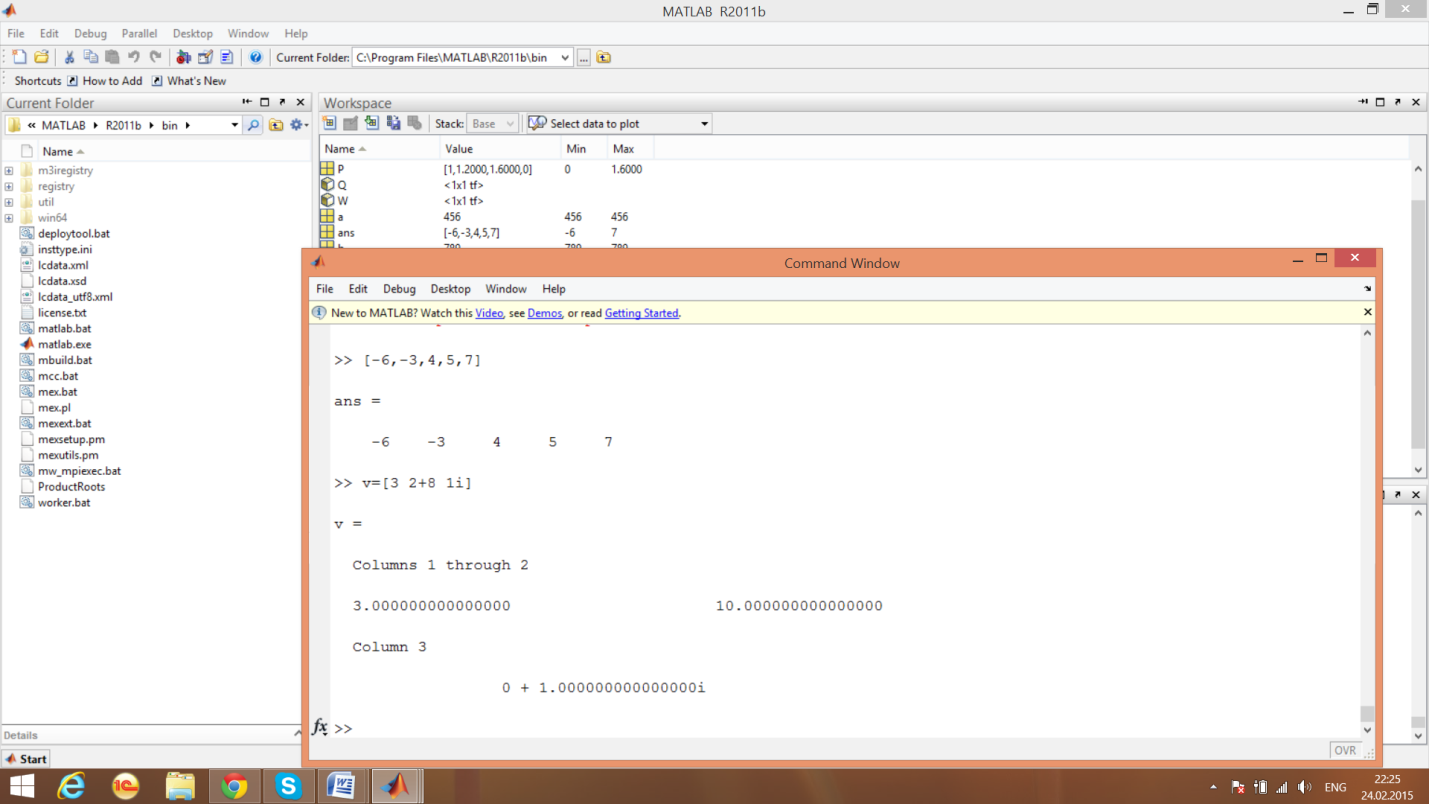
пример 2

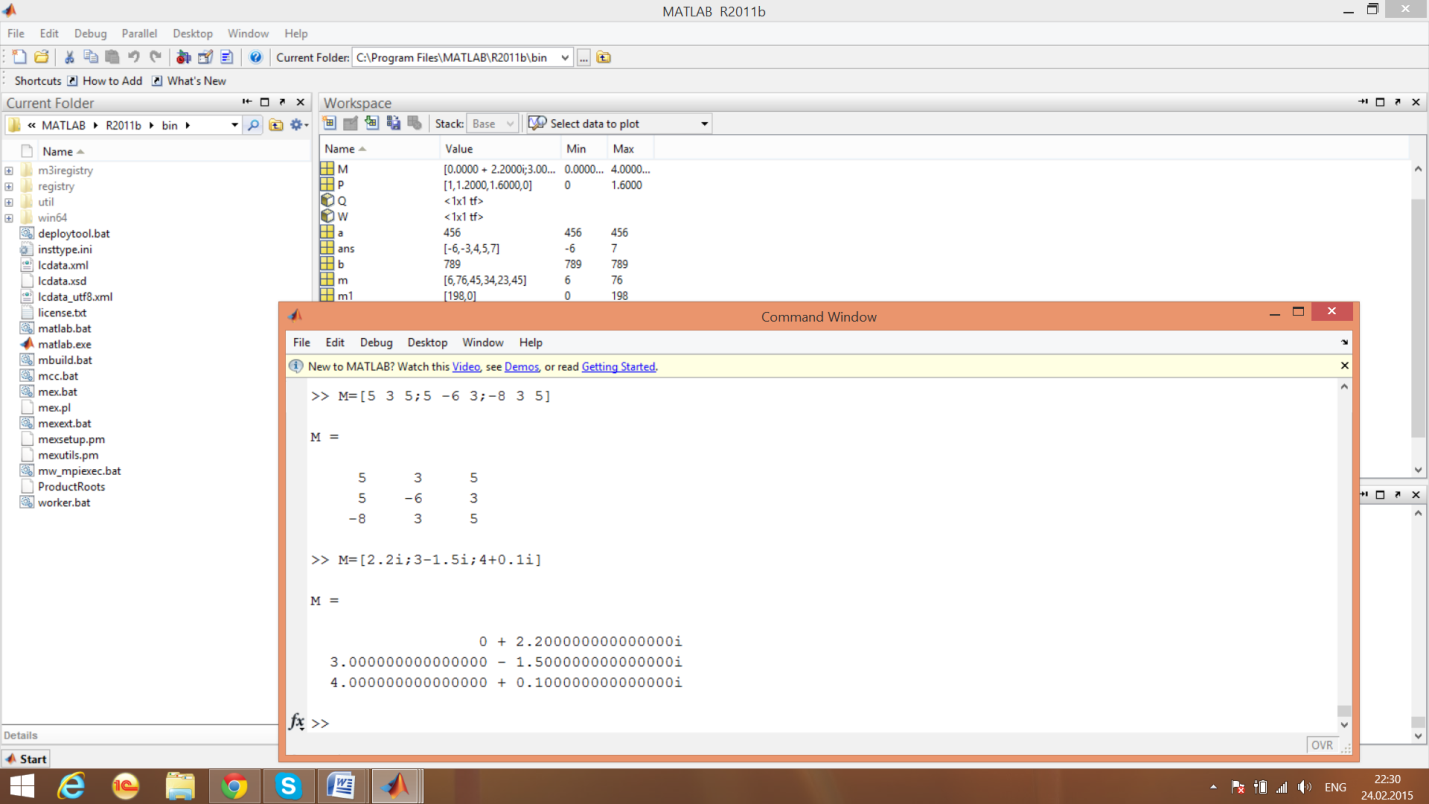
Пример 3

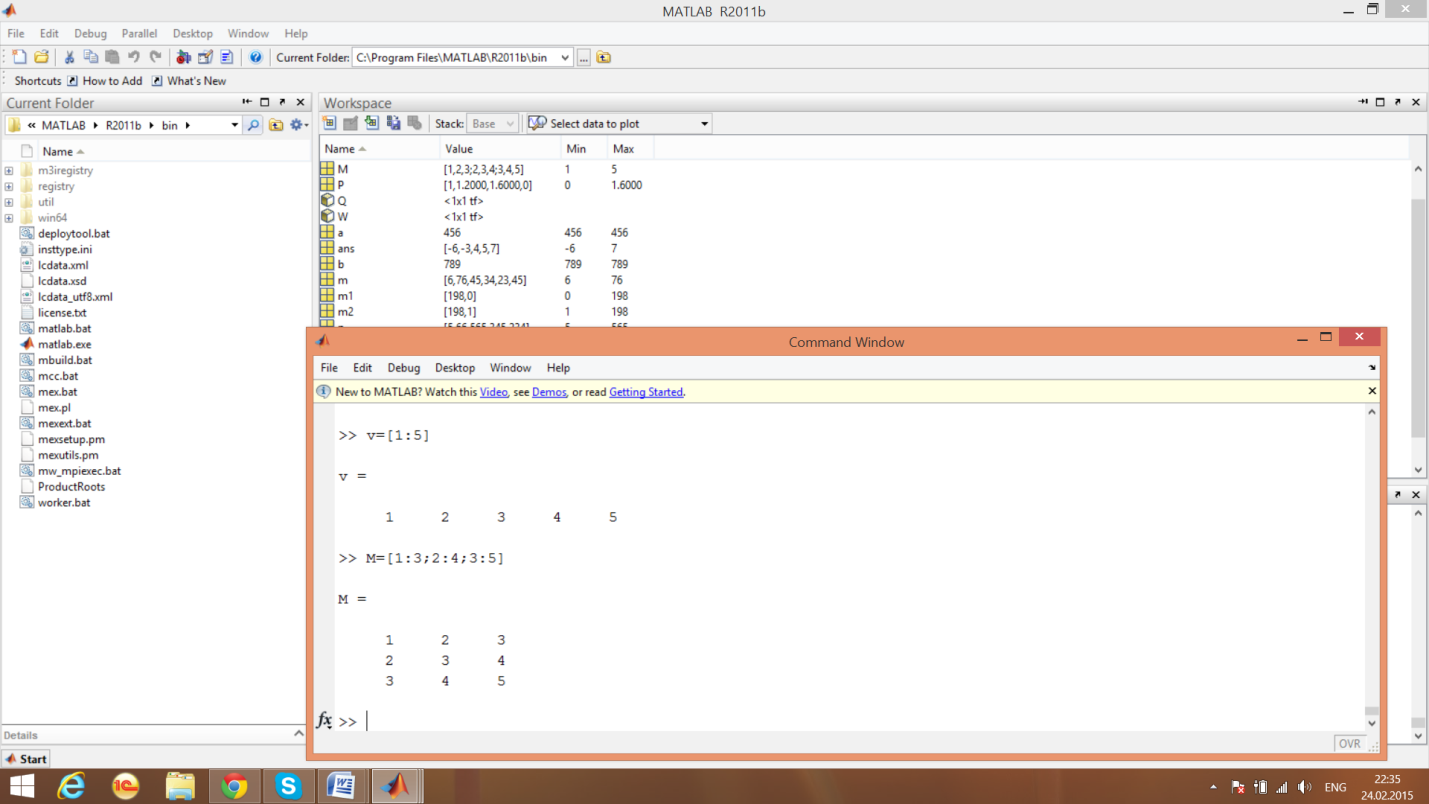
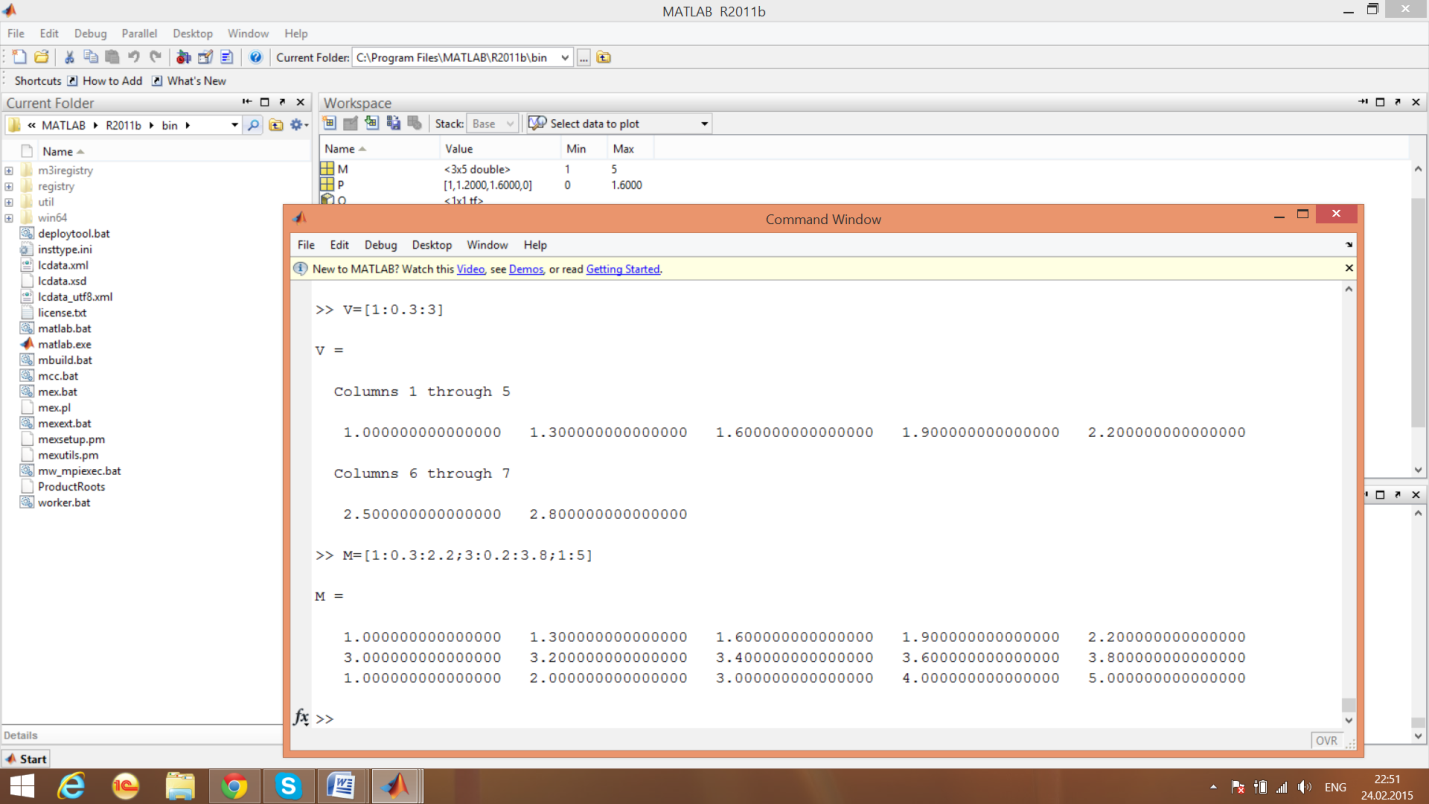
Пример4

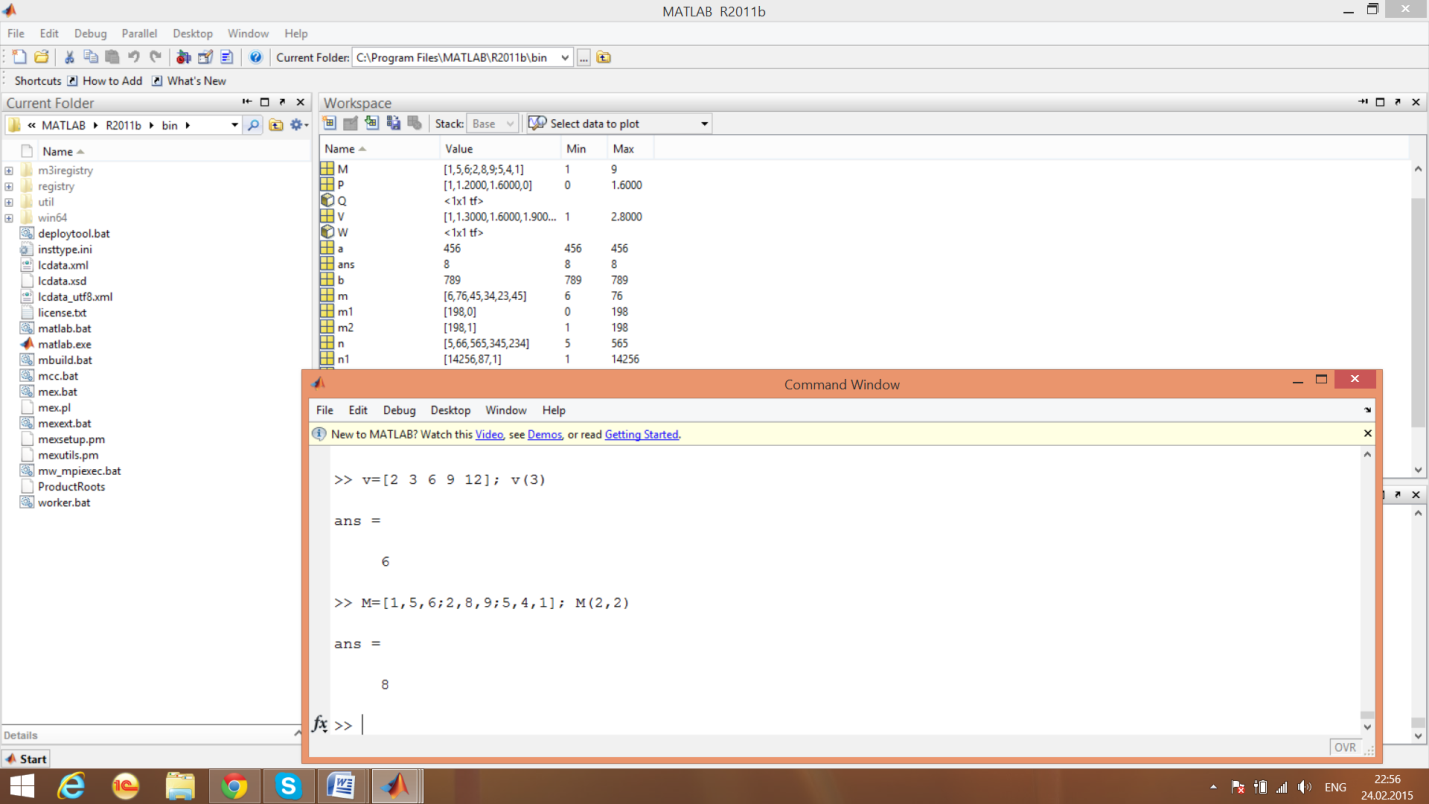
пример 5

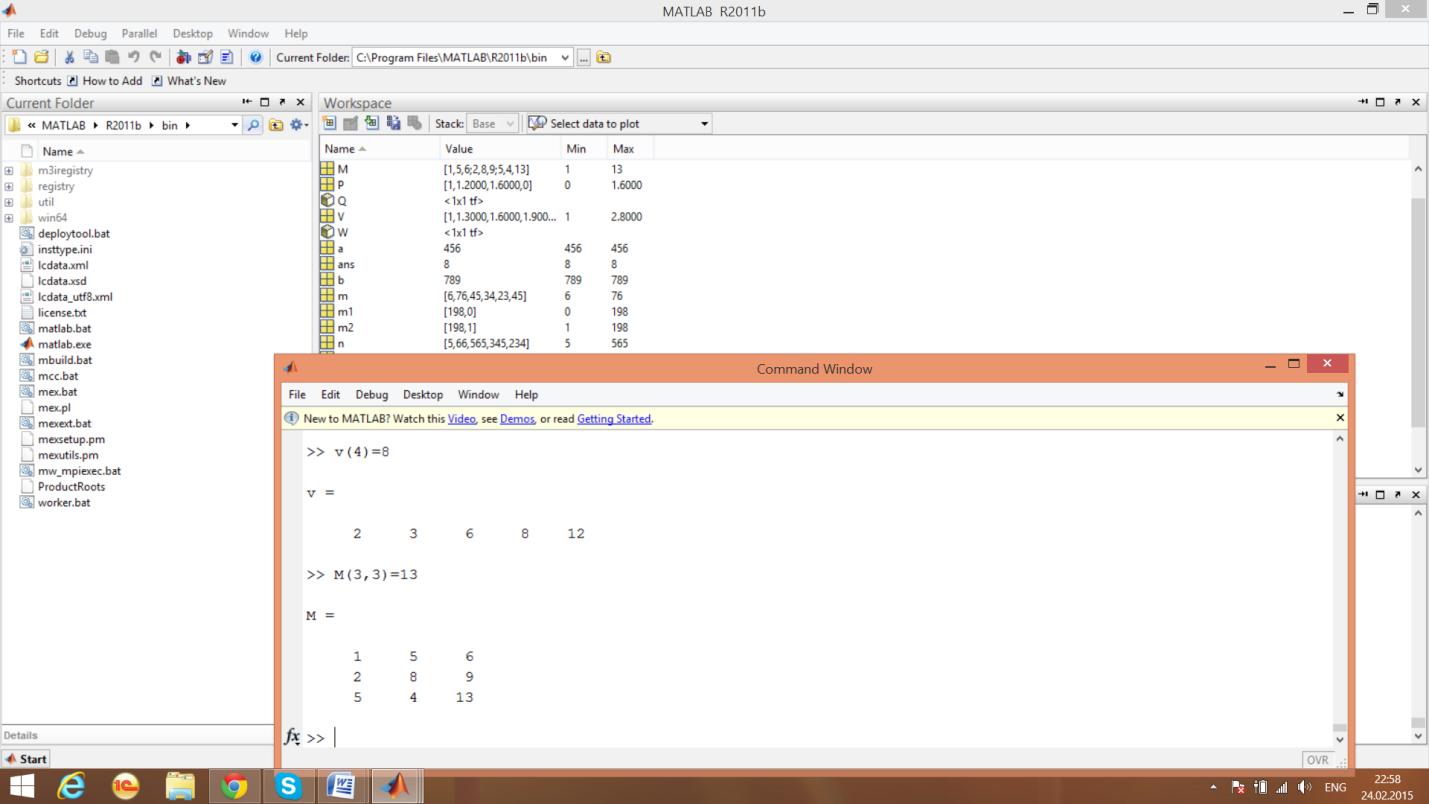
пример 6

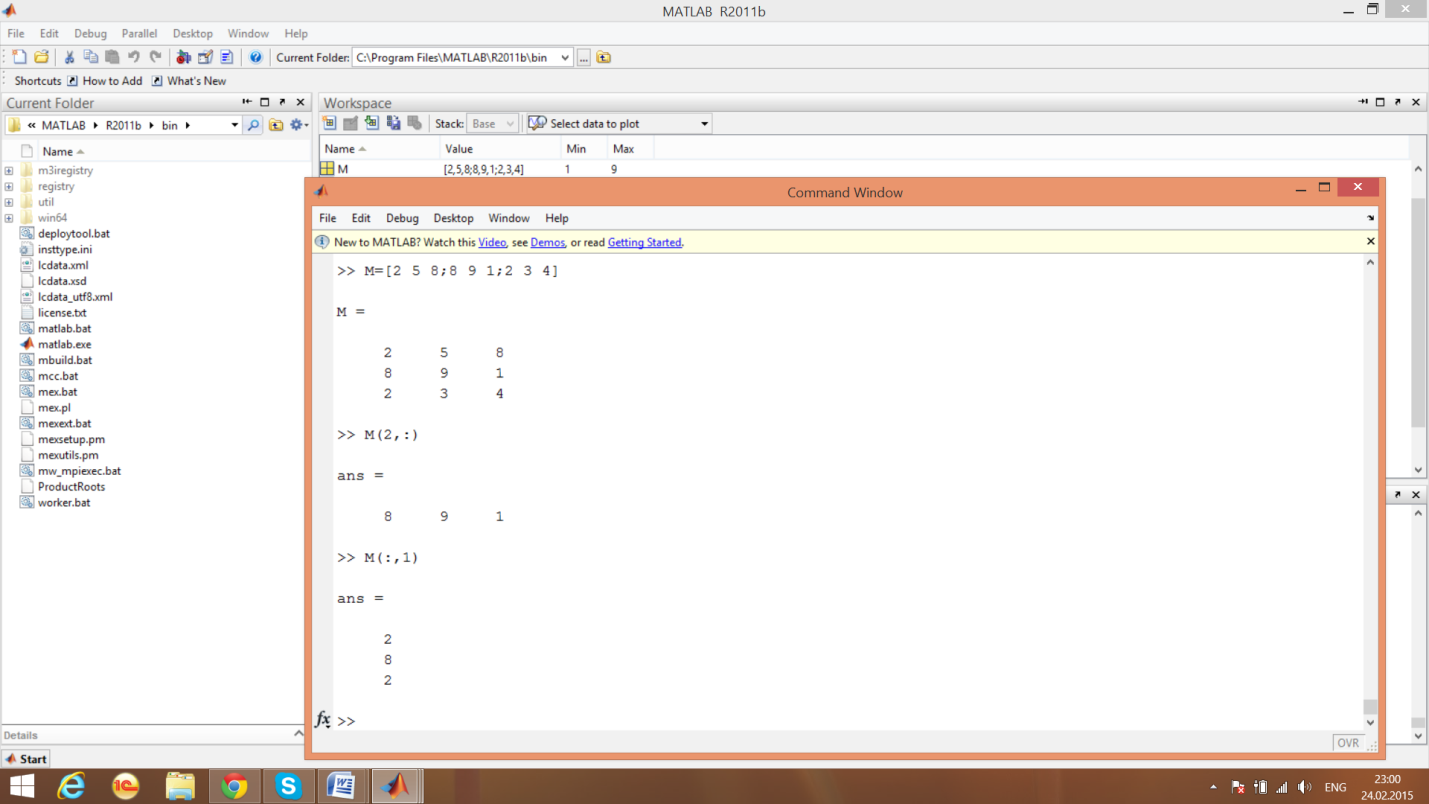
пример 7

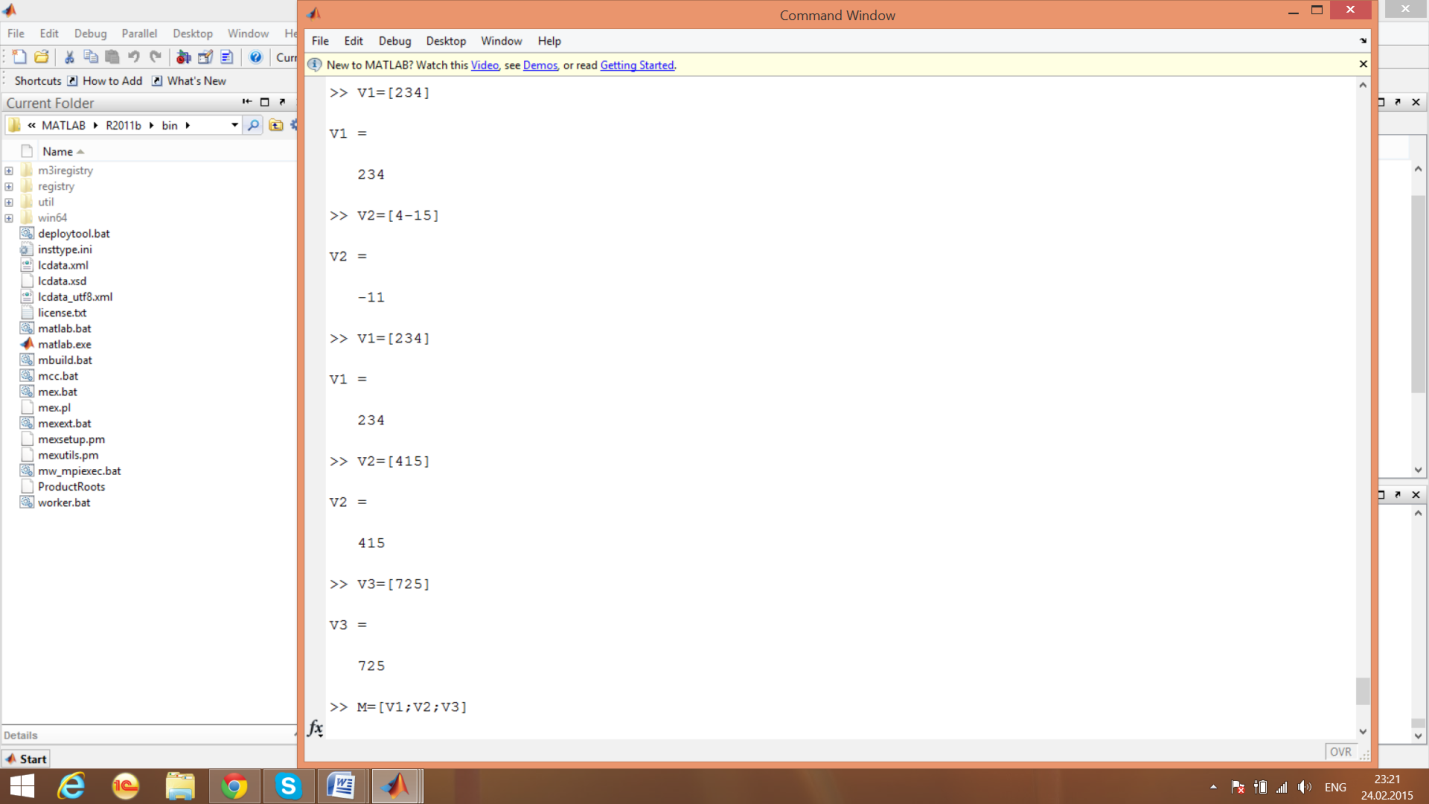
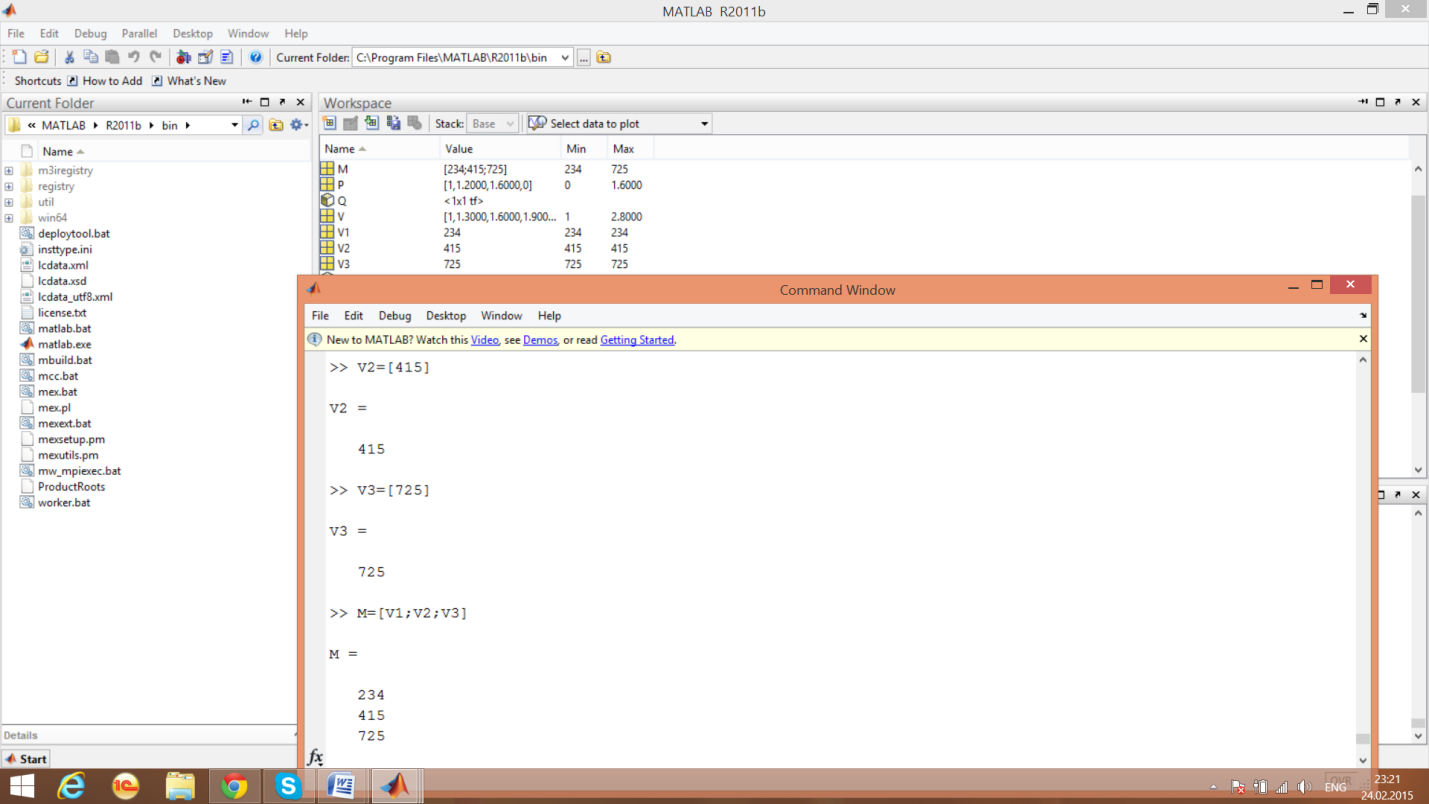
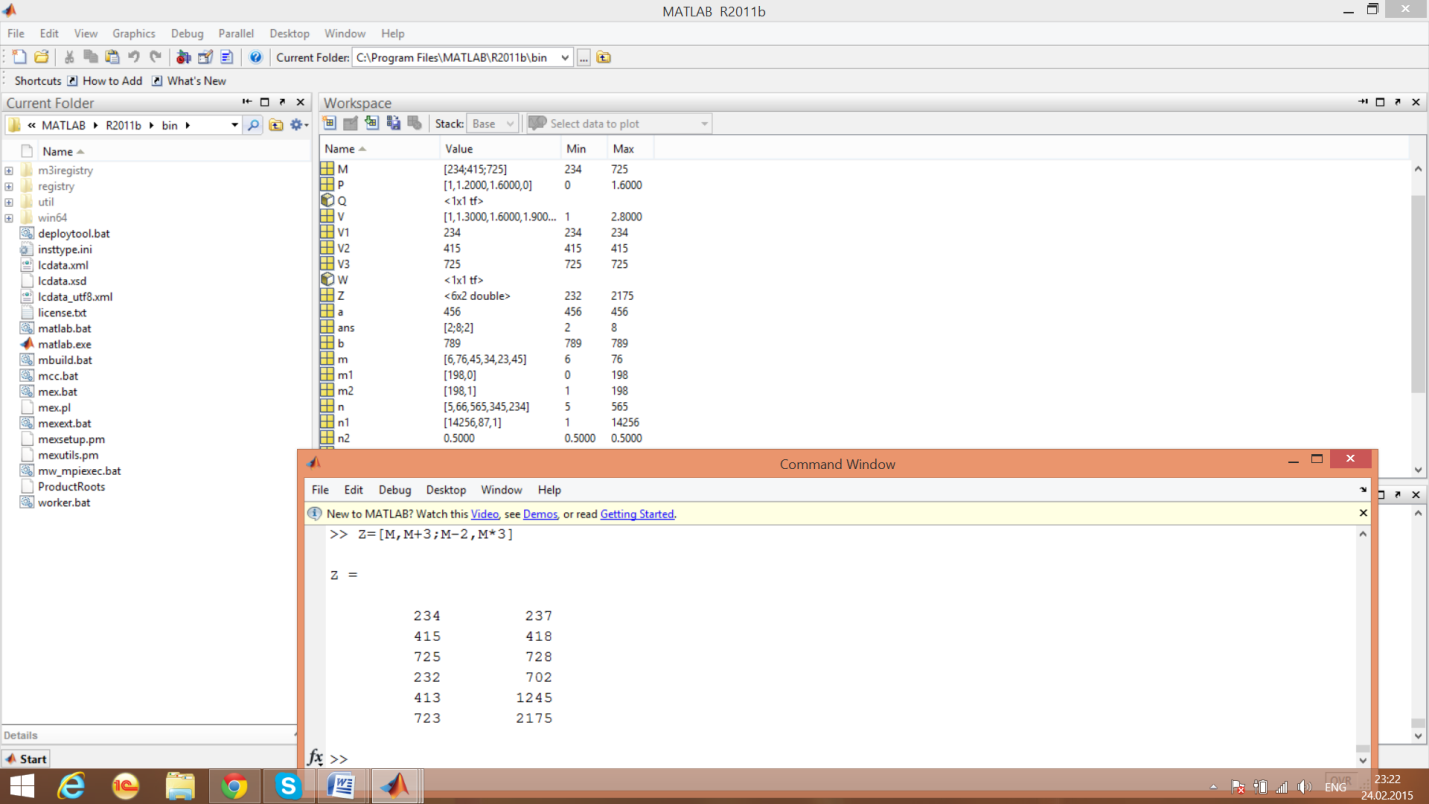
3. Математические операции с векторами и матрицами

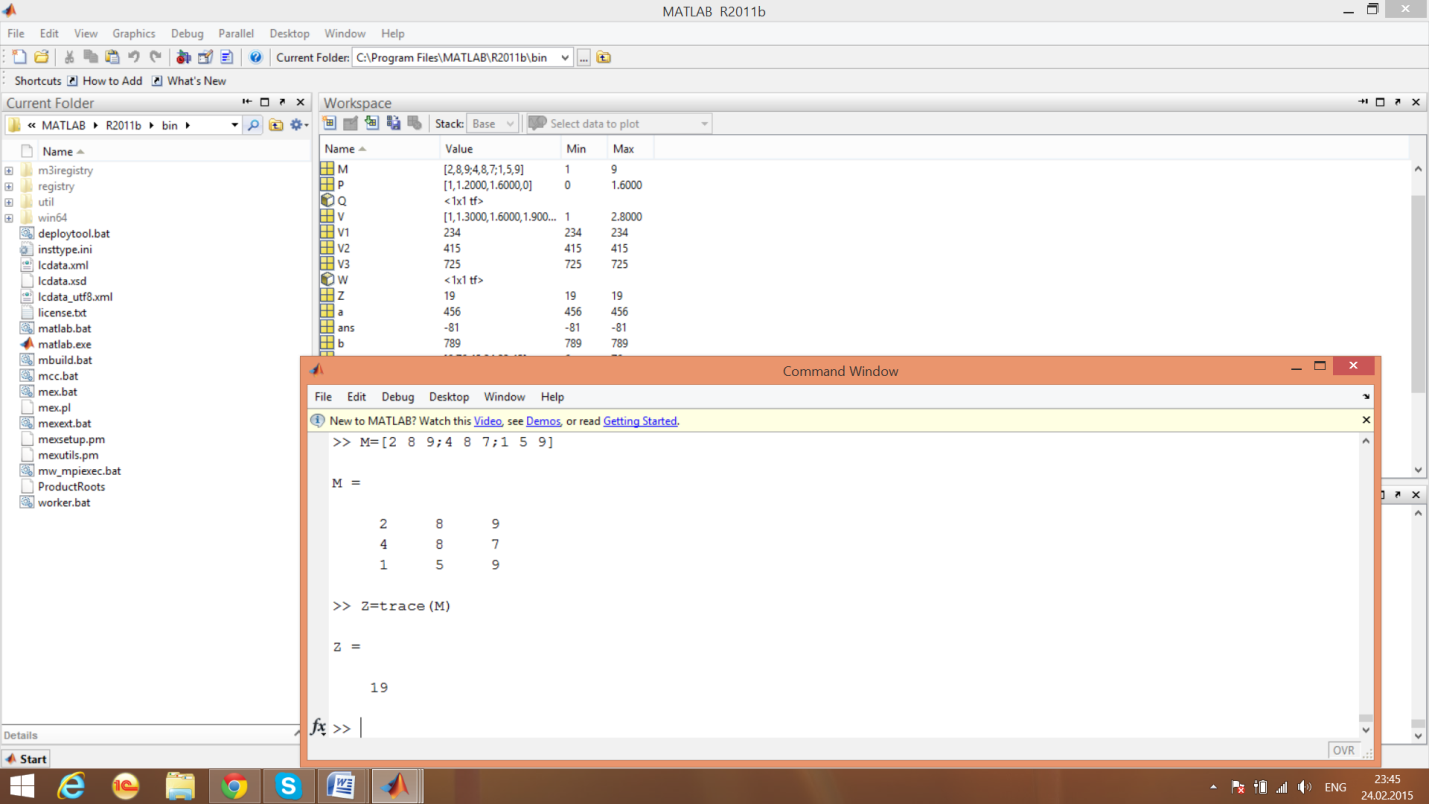
Определитель матрицы

пример 8

???

пример 9

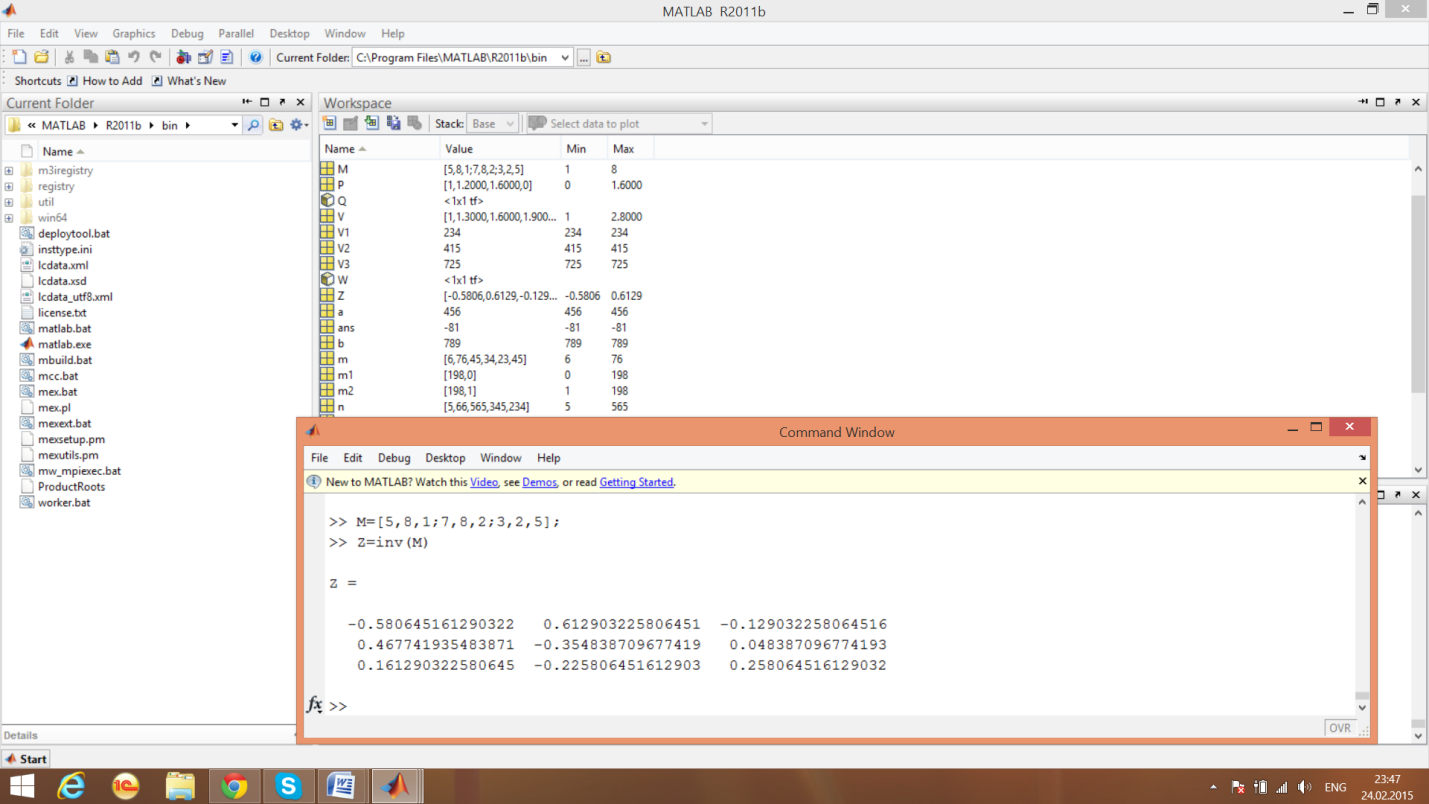
Обратная матрица

пример 11

Единичная матрица

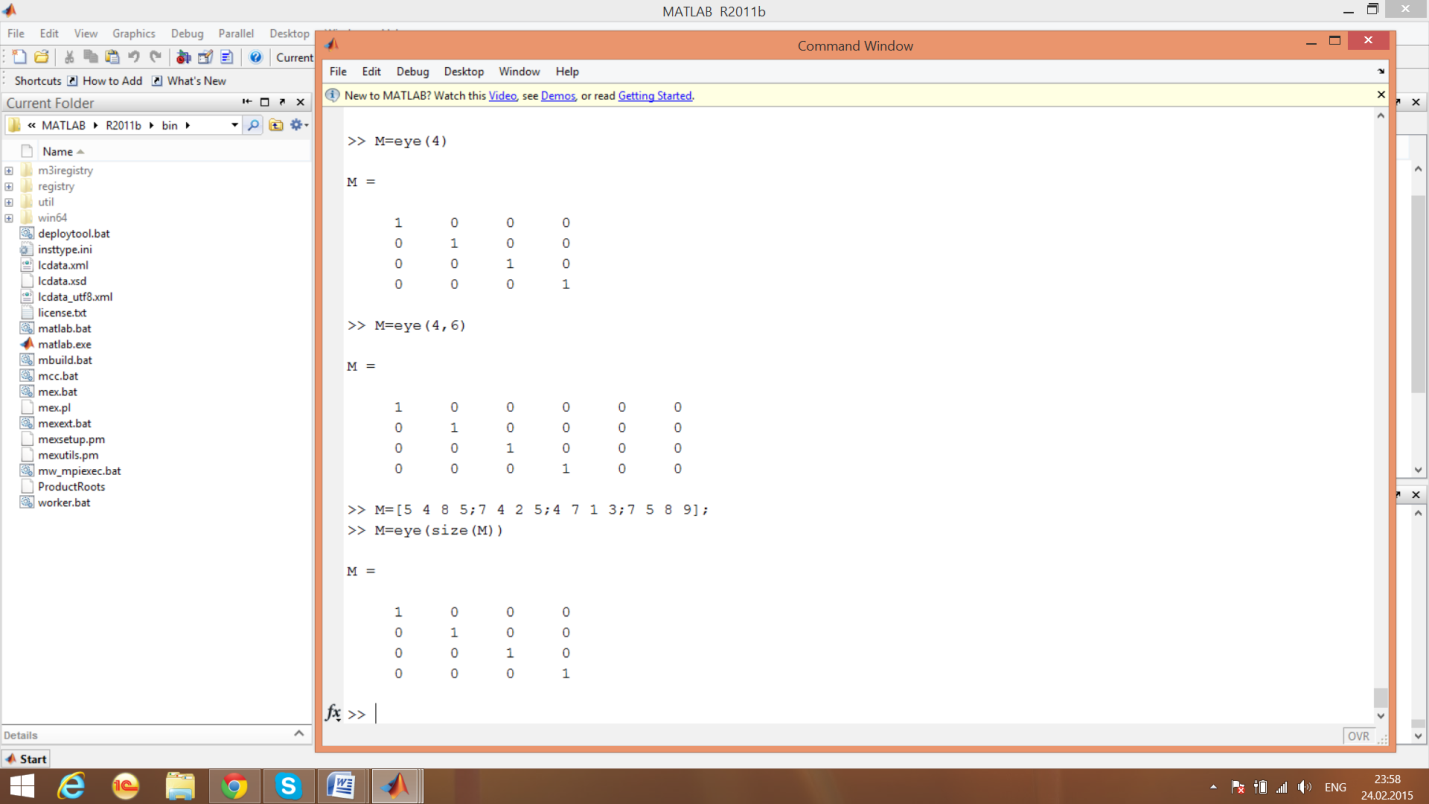пример 12

Образование матрицы с единичными элементами

пример 13

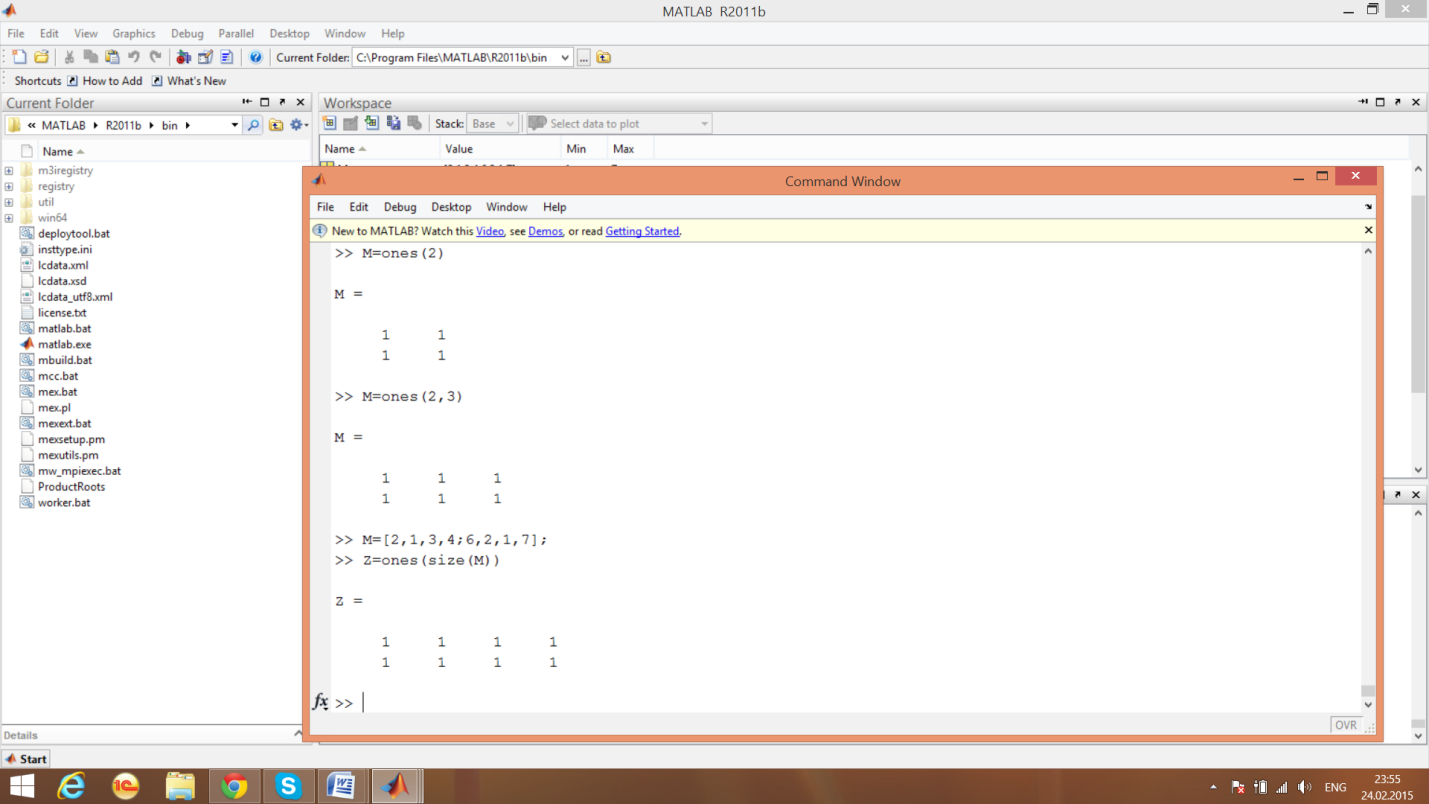
пример 14

Образование матрицы с нулевыми элементами

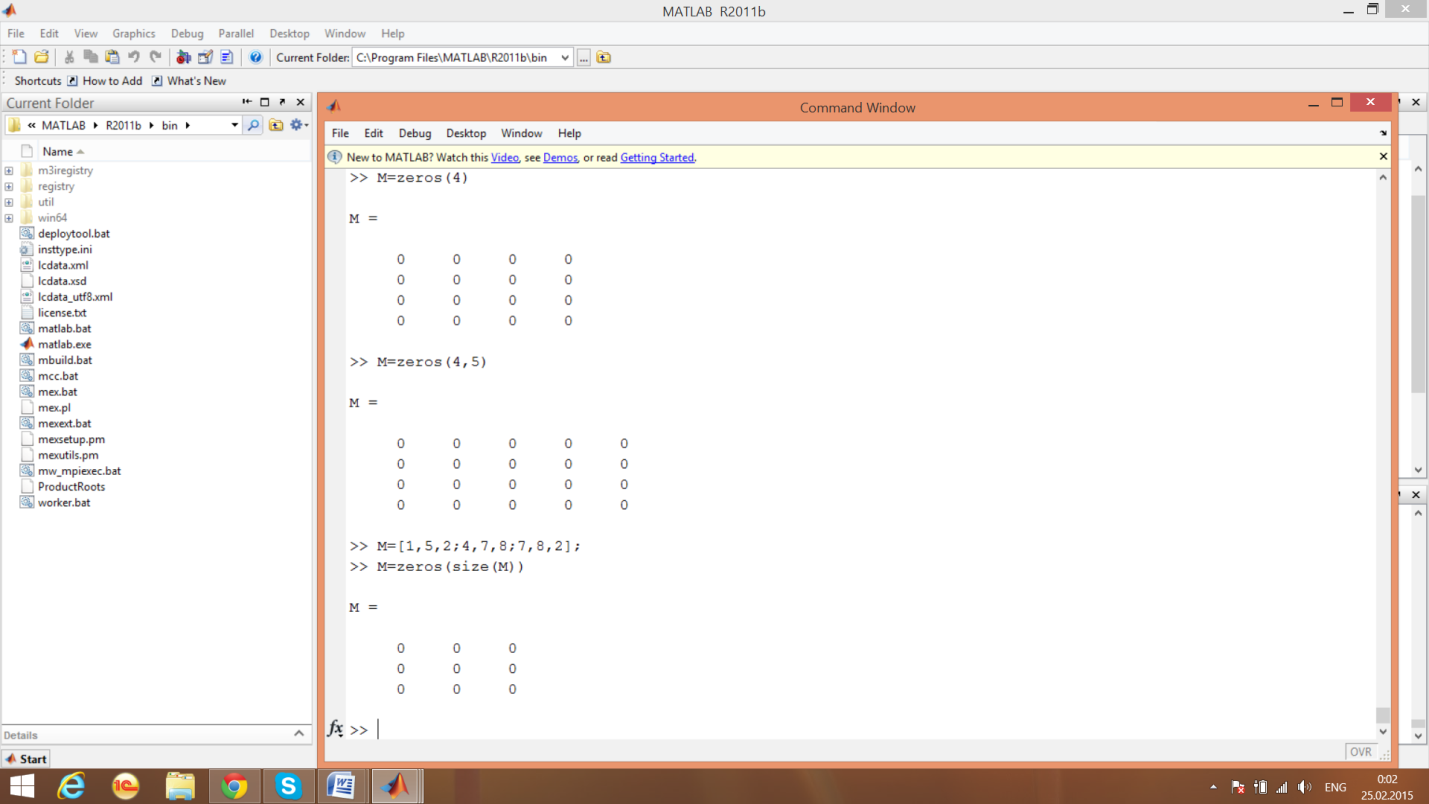
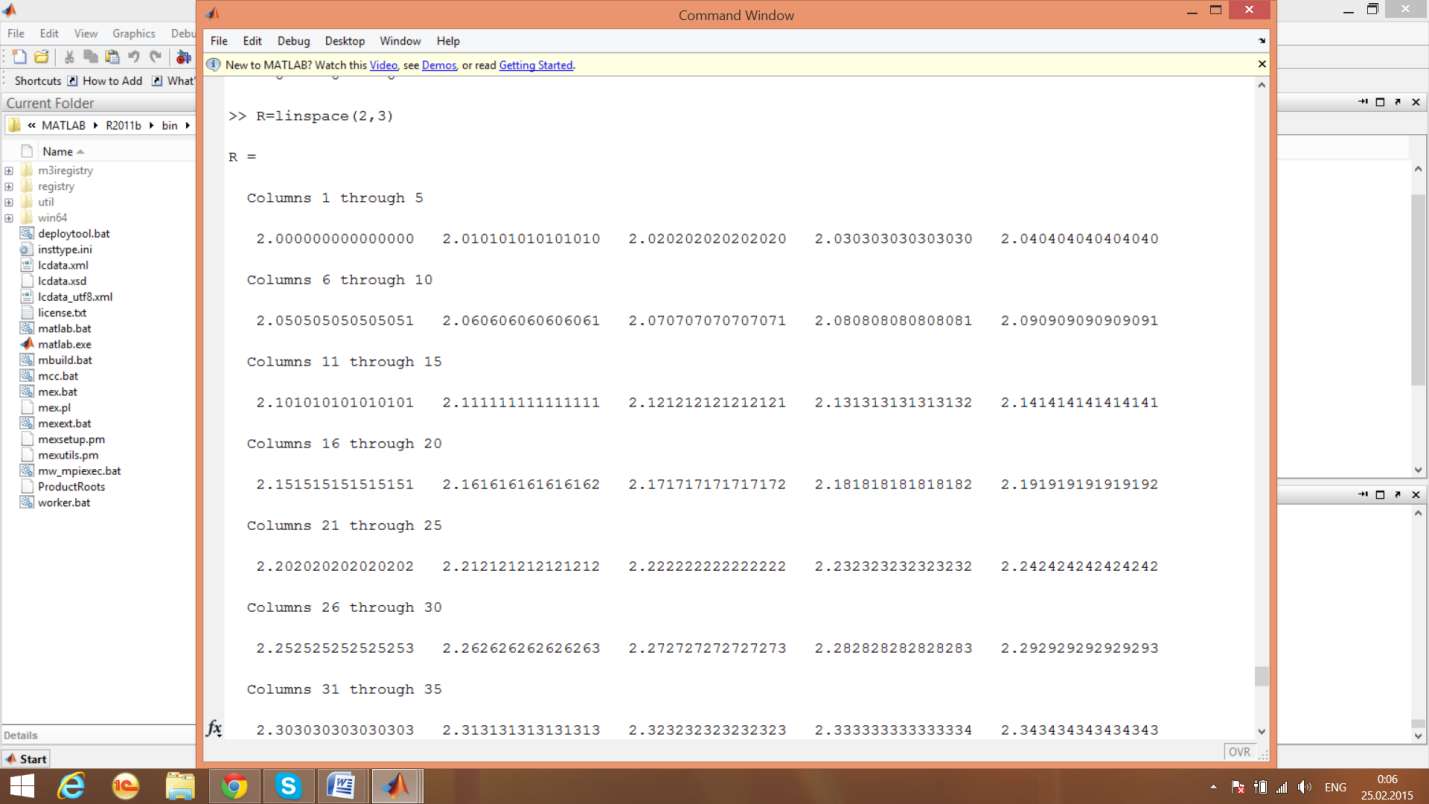
Вектор равностоящих точек

пример 15

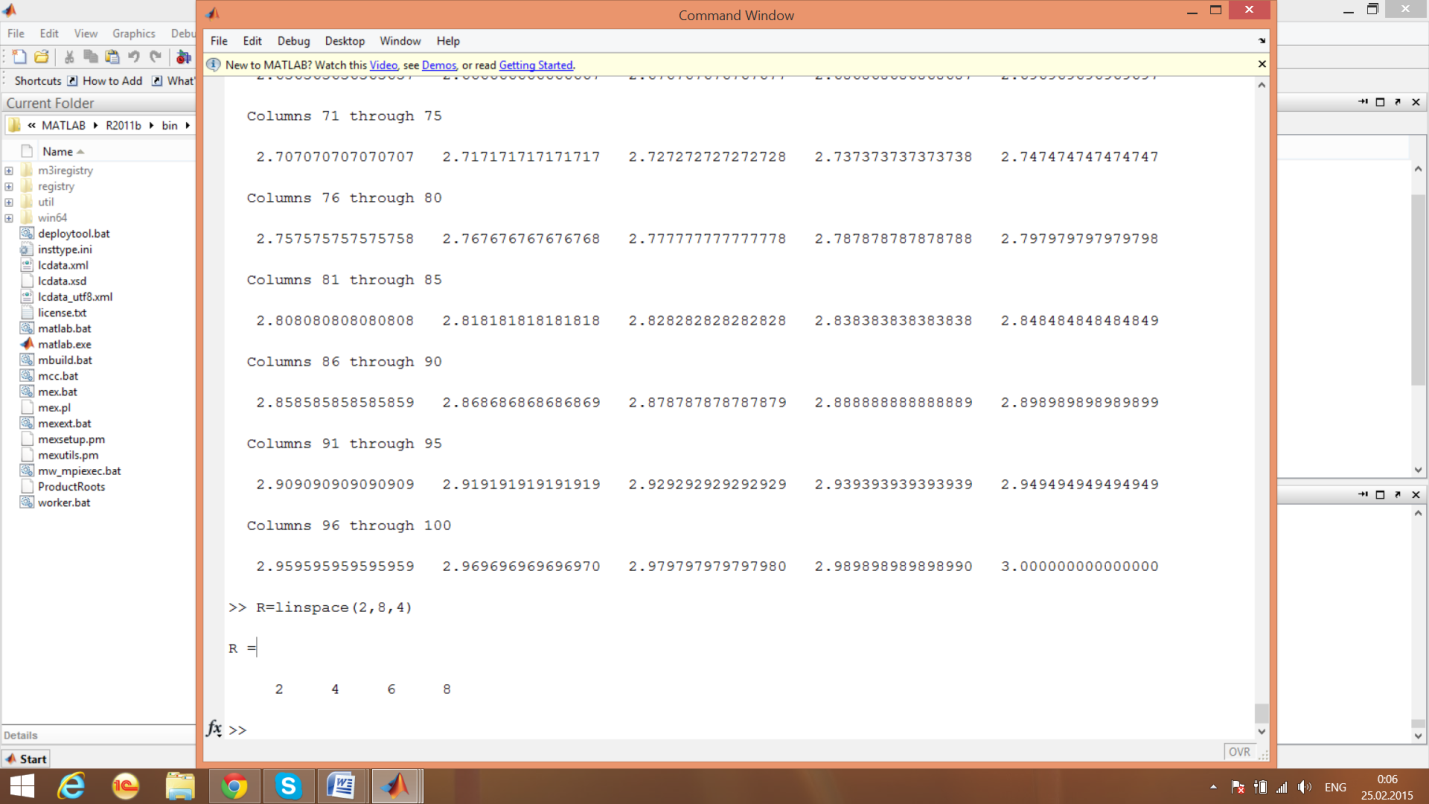
Перестановка элементов матрицы

пример 16