
Физика_Контр№3Вар№5
.pdfФизика Контрольная работа №3 Вариант №5
№№5, 15, 25, 35, 45, 55, 65, 75
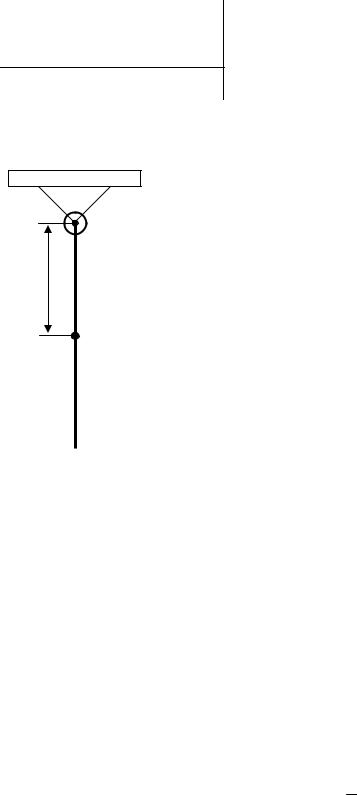
5. Физический маятник представляет собой тонкий стержень, подвешенный за один из его концов. При какой длине стержня период колебаний этого маятника будет равен 1 с?
Дано:
Т =1 с
Найти: l =?
Решение:
ось вращения |
l/2
Момент инерции стержня относительно его середины (оси, проходящей через центр инерции):
I = |
ml2 |
(1) |
1 |
12 |
|
|
|
где m −масса стержня, l − длина стержня.
По теореме Штейнера (по теореме о переносе осей инерции) момент инерции тела I относительно произвольной оси равен сумме момента инерции этого тела I0 относительно оси, проходящей через центр инерции тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат
расстояния между осями, т.е. в данном случае a = 2l .
2
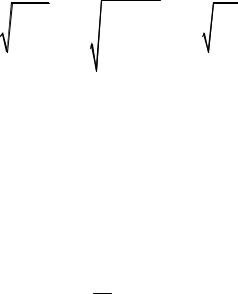
Момент инерции стержня относительно его конца:
|
l |
2 |
|
ml2 |
|
ml2 |
|
4ml2 |
|
ml2 |
||
I = I0 |
+ m |
|
|
= |
|
+ |
|
= |
|
= |
|
|
2 |
12 |
4 |
12 |
3 |
||||||||
|
|
|
|
|
|
|
||||||
Период колебаний физического маятника:
T = 2π |
I |
= 2π |
ml2 |
|
|
= 2π |
2l |
mga |
3mg |
l |
|
3g |
|||
|
|
|
|
||||
|
|
|
2 |
|
|
|
где g −ускорение свободного падения.
Из (3) находим: |
|
|
|
|
|
|
|
||||
|
T 2 |
3g |
|
|
1 с 2 |
3 9,8 |
м |
|
|
||
|
2 |
|
|
||||||||
l = |
|
|
|
= |
|
|
|
|
с |
|
= 0,37 м |
|
2 |
2 |
|
|
|||||||
|
2π |
|
|
2π |
|
|
|
|
|||
Проверим размерность формулы (4):
[l]=[T ]2 [g]= c2 cм2 = м
Вычисления:
|
1 2 |
3 9,8 |
|
(м) |
||
l = |
|
|
|
2 |
= 0,37 |
|
|
||||||
|
2π |
|
|
|
||
Ответ: l = 0,37 м.
(2)
(3)
(4)
3

15. В среде (ε =3; µ =1) распространяется плоская электромагнитная волна. Амплитуда напряженности магнитного поля волны 0,5 А/м. На ее пути перпендикулярно направлению распространения расположена поглощающая поверхность, имеющая форму круга радиусом 0,1 м. Чему равна энергия поглощения этой поверхности за время t =30 с? Период волны Т t.
Дано:
ε=3
µ=1
H = 0,5 А/ м r = 0,1 м
t =30 с
T t
Найти: W =?
Решение:
Плотность потока энергии электромагнитной волны определяется вектором Пойнтинга:
р = |
|
|
|
(1) |
Е |
×Н |
|||
где Е и Н −векторы напряженности электрического и магнитного по-
лей. Учитывая, что векторы Е и Н электромагнитной волне взаимноперпен-
дикулярны, для модуля вектора р получим: |
|
р = Е Н |
(2) |
Т.к. величины Е и Н в каждой точке волны меняются со временем по гармоническому закону, находясь в одинаковых фазах, то мгновенное значе-
ние р равно: |
|
|
|
|
|
|
|
|
p = E |
sinωt H |
m |
sinωt = E |
H |
m |
sin2 |
ωt |
(3) |
m |
|
m |
|
|
|
|
||
Энергия, переносимая через площадку S, перпендикулярную направ-
лению распространения волны, в единицу времени:
4
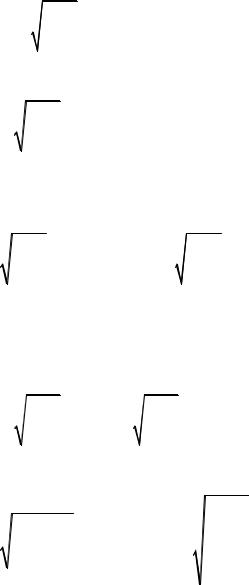
dW |
= ∫pdS = P S = S Em Hm sin2 ωt |
(4) |
dt |
S |
|
Учитывая, что в электромагнитной волне:
1 |
ε εE2 |
= |
1 |
µ |
µH 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5) |
|||||
2 |
0 |
m |
|
|
2 |
0 |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
ε0 −диэлектрическая |
постоянная; |
ε −диэлектрическая проницае- |
||||||||||||||||||||||||||||
мость среды; |
µ0 −магнитная постоянная; |
|
|
µ −магнитная проницаемость сре- |
|||||||||||||||||||||||||||
ды. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из (5): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Em = Hm |
|
µ0 µ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6) |
|||||
|
ε ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставим (6) в (4): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
dW |
= |
µ0µ H |
2 S sin2 ωt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7) |
|||||||||||
dt |
|
ε ε |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Энергия, переносимая волной за время t или энергия поглощения, рав- |
|||||||||||||||||||||||||||||||
на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
µ |
µ |
|
|
|
t |
|
|
|
|
|
|
µ |
µ |
|
|
|
|
t |
|
sin 2ωt |
|
|
|||||||
|
|
|
2 |
|
∫ |
|
2 |
|
|
|
|
2 |
|
|
|
|
|||||||||||||||
W = |
|
0 |
|
HmS |
sin |
|
|
ωtdt = |
0 |
|
HmS |
|
|
− |
|
4ω |
|
(8) |
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
ε ε |
|
|
|
|
|
|
|
|
|
ε ε |
|
|
|
|
2 |
|
|
|
|
||||||||||
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по условию задачи T t, |
поэтому |
|
t |
sin 2ωt ; |
тогда (учитываем, что |
||||||||||||||||||||||||||
2 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4ω |
|
|
|||||
площадь поглощающей поверхности S =πr2 ): |
|
|
|
|
|||||||||||||||||||||||||||
W = |
1 |
µ0µ H |
2 St = |
|
1 |
µ0µ H 2πr2t |
|
|
|
|
|
|
|
|
|
|
(9) |
||||||||||||||
|
|
2 |
ε ε |
|
m |
|
|
2 |
ε ε |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Проверим размерность формулы (9): |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
[µ0 ][µ] |
|
|
|
|
2 |
|
2 |
|
Гн |
1 |
|
|
А2 |
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
[r] [t]= |
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
м2 |
|
|
|
|
|
||||||||||||||
W = [ε0 ][ε] Hm |
|
|
Ф |
1 |
м с = |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
м |
|
|
|
|
|
|
|
|
|
|
|
||||
5
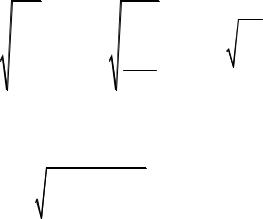
|
Вб |
|
|
|
В с |
|
|
|
В2 |
|
|
|
B |
|
|
|
|
= |
А |
А |
2 |
с = |
А |
|
А |
2 |
с = |
А |
2 |
с = |
А |
2 |
с = |
||
Кл |
|
А |
с |
|
A2 |
|
A |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ВВ
=В А с = В Кл = Дж
Вычисления:
W = |
1 |
4π 10−7 1 |
(0,5)2 π (0,1)2 30 с = 25,61 (Дж) |
|
2 |
8,85 10−12 3 |
|||
|
|
Ответ: W = 25,61 Дж.
6
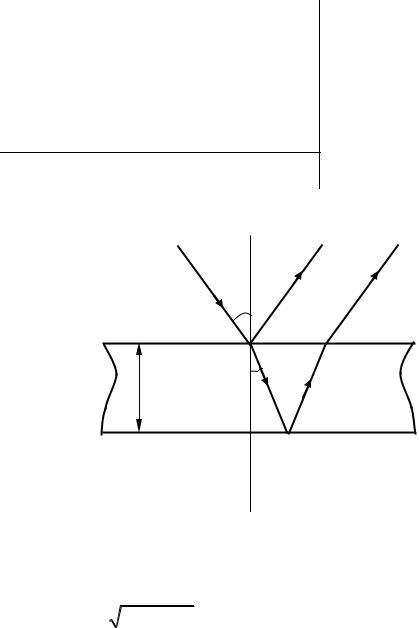
25. Для устранения отражения света на поверхность стеклянной линзы наносится пленка вещества с показателем преломления 1,3 меньшим, чем у стекла. При какой наименьшей толщине этой пленки отражение света с длиной волны 0,48 мкм не будет наблюдаться, если угол падения лучей 30°?
Дано:
n1 =1,3
п1 > n2
λ= 0,48 мкм = 0,48 10−6 м
i=30°
Найти: dmin =?
Решение:
i
d |
r |
n1
п2
Оптическая разность хода световых волн, отраженных от верхней и нижней поверхностей пленки, находящейся в воздухе (п1 > n2 ):
∆ = 2d n2 −sin2 i |
(1) |
|
где |
i −угол падения света; n −показатель |
преломления пленки; |
d −толщина пленки. |
|
|
Условие минимума отражения: |
|
|
∆ = |
λ (2k +1) |
(2) |
|
2 |
|
7
где k = 0, 1, 2, ... – порядок минимума.
Из (2):
2d |
n2 −sin2 i = λ (2k +1) |
|
|
|
(3) |
||||||
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d будет минимально при k = 0 : |
|
|
|
|
|||||||
dmin |
= |
|
λ |
= |
|
|
0,48 10−6 м |
= 0,1 |
10 |
−6 |
м |
4 |
n2 −sin2 i |
|
4 |
1,32 −sin2 30° |
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
Ответ: dmin = 0,1 10−6 |
м. |
|
|
|
|
|
|||||
8
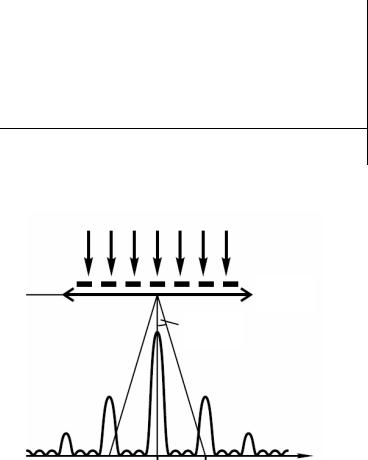
35. Постоянная дифракционной решетки равна 5 мкм. Определить наибольший порядок спектра, общее число главных максимумов в дифракционной картине и угол дифракции в спектре четвертого порядка при нормальном падении монохроматического света с длиной волны 0,625 мкм.
Дано:
d =5 мкм =5 10−6 м k = 4
λ = 0,625 мкм = 0,625 10−6 м
Найти: kmax =? М =? ϕ4 =?
Решение:
ЛИНЗА
φ
ЭКРАН
Условие наблюдения максимумов:
d sinϕ=kλ |
(1) |
где d −постоянная решетки; k − порядок максимума; ϕ −угол откло-
нения лучей, соответствующий максимуму; λ −длина волны, падающего света.
Наибольший порядок максимумов:
kmax |
= Целоечислоот d sin 900 |
|
= Целоечислоот |
5 мкм 1 |
=8 |
|
|||||
|
λ |
|
|
0,625 мкм |
|
9
Определим общее число максимумов дифракционной картины, полученной посредством дифракционной решетки. Влево и вправо от центрального максимума будет наблюдаться по одинаковому числу максимумов, равному kmax , т. е. всего 2kmax . Если учесть также центральный нулевой максимум,
получим общее число максимумов:
M = 2k +1 = 2 8 +1 =17
Угол дифракции в спектре |
четвертого порядка: |
||||||
ϕ4 |
|
4λ |
|
4 |
0,625 мкм |
=30° |
|
= arcsin |
|
= arcsin |
|
5 мкм |
|
||
|
|
d |
|
|
|
|
|
Ответ: kmax =8; М =17; ϕ4 =30°.
10
