Мгновенное значение мощности.

При синусоидальных токах и напряжениях

, как и для любой цепи.

Подставив в это выражение синусоидальный ток через какой-либо участок цепи и напряжение на этом участке, получим, приняв, что ток отстает от напряжения на угол :

.

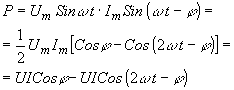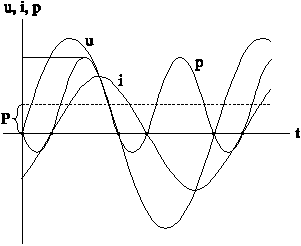
Рис. 4-8

Из формулы и осциллограммы видно, что мгновенная мощность состоит из двух слагаемых: одно, не зависящее от времени, - постоянная составляющая, а другое - синусоидальная функция времени двойной частоты. График p проходит через ноль в точках, где пересекают ось абсцисс либо ток, либо напряжение (рис. 4-8).

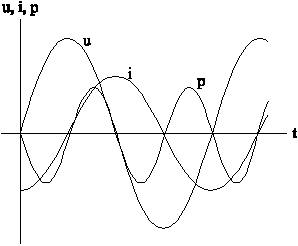
Интересно отметить, что если ток и напряжение сдвинуты по фазе на угол (чисто емкостная или чисто индуктивная цепь), то первое слагаемое равно нулю (рис. 4-9).

Из формулы:

.

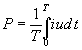следует, что для измерения мощности требуется иметь прибор, перемножающий две функции времени и вычисляющий среднее значение (постоянную составляющую) такой функцию.

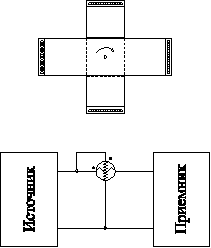
Для измерения мощности в реальных цепях применяют электродинамические ваттметры. Они состоят из двух магнитно-связанных катушек, одна из которых может вращаться вокруг оси. С подвижной катушкой связана стрелка, показывающая на шкале угол ее отклонения от нулевого положения, которое поддерживается специальной пружинкой.

Противодействующий момент пружинки по закону Гука пропорционален углу отклонения стрелки - .

Вращающий момент определяется изменением энергии запасенной системой при пропускании токов через катушки при повороте подвижной катушки

.

Равновесие достигается при .

.

Энергия, запасенная системой двух катушек:

.

Первые два слагаемых от угла не зависят

.

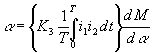Т.к. механическая инерционность системы приведет к тому, что угол отклонения стрелки будет пропорционален среднему значению момента.

Таким образом, если через одну из катушек пропускать ток пропорциональный току приемника, а через другую - пропорциональный его напряжению, получим (в предположении ), что уголбудет пропорционален активной мощности

.

На рис. 4-11 показана схема включения ваттметра. Точками (или звездочками) отмечены зажимы, которые следует объединить, т.к. направление вращающегося момента зависит от согласования направлений тока и напряжения.

13. Комплексный метод расчета при последовательно-параллельном соединении двухполюсников. Построение векторной диаграммы.

(рассмотрим поподробнее) (рис. 4-18) при

.

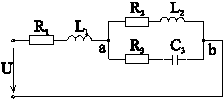
Рис. 4-18

Комплексные сопротивления двухполюсников:

,

,

.

Сопротивление двухполюсника аb:

.

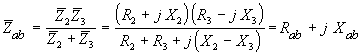Эквивалентное сопротивление всей цепи:

.

Входной ток - ток через первый двухполюсник:

, где 

; ;

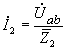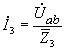
или по формуле делителя тока:

; .

Мощности:

; ;;

; ;.

Мощности источника U:

;

.

“Успех” построения векторной диаграммы (желательно не зависимо от алгебраического расчета) определяется порядком построения (рис. 4-19).

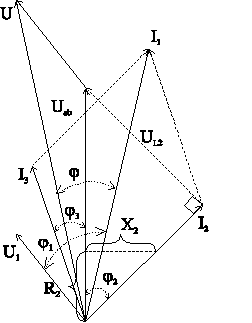
Рис. 4-19

1. Возьмем за основу вектор произвольной величины.

2. Вектор тока отстает от него на угол.

3. Вектор тока опережает напряжениена угол.

Для построения углов нет необходимости их вычислять. Достаточно построить треугольники сопротивлений. Соотношение между величинами векторов инадо соблюсти в соответствии с пропорцией:.

4. Сложив вектора ив соответствии с первым законом Кирхгофа, получим:.

5. Угол определит направление вектора напряжения, относительно тока, величина вектораопределится из соотношения.

6. Геометрическим сложением определим , остается задаться конкретным масштабом, приравняв, и выбрать масштаб тока. Полученная диаграмма с точностью до геометрических построений дает ответы обо всех величинах токов и напряжений и их относительных фазах. Например, перпендикуляр из конца векторана направление токадаст напряжение на катушке. Векторную диаграмму можно использовать для проверки правильности алгебраических расчетов. Например, уголмежду токоми входным напряжениемдолжен быть равен.