
- •Оглавление
- •1 .Электрическая цепь. Идеальные элементы электрических цепей и их свойства.
- •2 Схема электрической цепи. Топология. Матрицы соединений.
- •Уравнения Кирхгофа для мгновенных значений токов и напряжений.
- •II Закон Кирхгофа
- •I закон Кирхгофа
- •II закон Кирхгофа
- •5. Расчет простых цепей при постоянных токах и напряжениях. Эквивалентные преобразования пассивных и активных двухполюсников.
- •6 .Метод эквивалентного генератора.
- •7. Уравнения равновесия для обобщенной ветви.
- •8. Принцип наложения и его применение при анализе цепей.
- •9. Баланс мощностей и потенциальная диаграмма в цепях постоянного тока.
- •10.Синусоидальные токи и напряжения, из изображения векторами и комплексными числами.
- •11. Двухполюсники при синусоидальных токах и напряжениях. Расчет цепей при различных соединениях двухполюсников. Векторные диаграммы.
- •I. Последовательное соединение двухполюсников (рис. 4-14)
- •II. Параллельное соединение двухполюсников (рис. 4-16).
- •III. Смешанное соединение
- •12. Активная, реактивная и полная мощность в цепях синусоидальных токов. Мгновенное значение мощности. Измерение мощности.
- •Мгновенное значение мощности.
- •13. Комплексный метод расчета при последовательно-параллельном соединении двухполюсников. Построение векторной диаграммы.
- •14. Матричная запись уравнений Кирхгофа и Ома для сложных цепей.
- •15. Метод узловых потенциалов. Вывод уравнений.
- •16. Система уравнений по методу контурных токов.
- •17. Уравнения по методу сечений для обобщенной модели двухполюсника.
- •18. Резонанс напряжений, частотные характеристики.
- •19. Резонансные явления в сложных цепях без потерь. Частотные характеристики.
- •Частотные свойства параллельного контура
- •1.Параллельное соединение glc.
- •20. Расчет электрических цепей при несинусоидальных периодических токах и напряжениях.
- •21.Активная мощность при несинусоидальных периодических токах и напряжениях.
- •22.Измерения при несинусоидальных периодических токах и напряжениях приборами различных систем.
- •23.Уравнения четырехполюсников.
- •24.Эквивалентные схемы четырехполюсников.
- •25.Экспериментальное определение параметров четырехполюсников при синусоидальных токах и напряжениях.
- •26.Последовательное соединение четырехполюсников. Регулярность.
- •27.Параллельное соединение четырехполюсников. Регулярность.
- •28.Смешанное соединение четырехполюсников. Регулярность.
- •1. Одноэлементный (последовательный) четырехполюсник (рис. 8-14).
- •30.Понятие об активном четырехполюснике.
- •31.Характеристические параметры четырехполюсника. Затухание.
- •32 .Круговые диаграммы для простых схем. Порядок построения круговой диаграммы в общем случае.
I. Последовательное соединение двухполюсников (рис. 4-14)
![]()

Рис. 4-14
По второму закону Кирхгофа
![]() ,
где
,
где ![]() ,
,
значит,
![]() .
.
![]() ;
; ![]() (
(![]() -
берется с учетом знака).
-
берется с учетом знака).
![]() ,
где
,
где ![]() .
.
Мощности:
![]() ,
,
![]() .
.
Если векторную диаграмму напряжений на двухполюсниках изобразить относительно общего тока в соответствии с топологией схемы, получим т.н. топографическую диаграмму, из которой легко определить напряжения между любыми точками схемы (рис. 4-15).
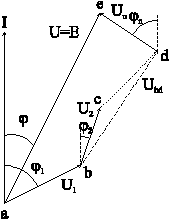
Рис. 4-15
Вычислив
при произвольном токе (например, ![]() )
напряжения на каждом элементе
)
напряжения на каждом элементе![]() и
построив векторную диаграмму, можно,
изменив масштаб
и
построив векторную диаграмму, можно,
изменив масштаб![]() в
соответствии с заданным, получить из
геометрических соотношений решение
всей задачи анализа.
в
соответствии с заданным, получить из
геометрических соотношений решение
всей задачи анализа.
II. Параллельное соединение двухполюсников (рис. 4-16).
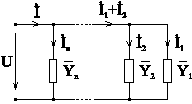
Рис. 4-16
Здесь удобно пользоваться характеристикой двухполюсников в виде проводимостей:
![]() .
.
По первому закону Кирхгофа
![]() .
.
Напомним,
что ![]() ,
если двухполюсник индуктивный (
,
если двухполюсник индуктивный (![]() )
и
)
и![]() ,
если двухполюсник емкостный (
,
если двухполюсник емкостный (![]() ).
).
Таким образом,
![]() ;
; ![]() ;
;![]() .
.
Топографическая диаграмма токов, построенная относительно общего напряжения, представлена на рис. 4-17.

Рис. 4-17
Из
топографической диаграммы удобно
находить токи в соответствующих
соединениях (например ![]() ).
).
Баланс мощности:
![]() ,
,
![]() .
.
III. Смешанное соединение
(рассмотрим поподробнее) (рис. 4-18) при
![]() .
.
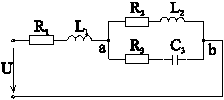
Рис. 4-18
Комплексные сопротивления двухполюсников:
![]() ,
,
![]() ,
,
![]() .
.
Сопротивление двухполюсника аb:
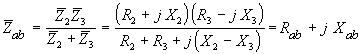 .
.
Эквивалентное сопротивление всей цепи:
![]() .
.
Входной ток - ток через первый двухполюсник:
![]() ,
где
,
где ![]()
![]() ;
;  ;
;
или по формуле делителя тока:
![]() ;
; ![]() .
.
Мощности:
![]() ;
; ![]() ;
;![]() ;
;
![]() ;
; ![]() ;
;![]() .
.
Мощности источника U:
![]() ;
;
![]() .
.
“Успех” построения векторной диаграммы (желательно не зависимо от алгебраического расчета) определяется порядком построения (рис. 4-19).

Рис. 4-19
1.
Возьмем за основу вектор ![]() произвольной
величины.
произвольной
величины.
2.
Вектор тока ![]() отстает
от него на угол
отстает
от него на угол![]() .
.
3.
Вектор тока ![]() опережает
напряжение
опережает
напряжение![]() на
угол
на
угол![]() .
.
Для
построения углов нет необходимости их
вычислять. Достаточно построить
треугольники сопротивлений. Соотношение
между величинами векторов ![]() и
и![]() надо
соблюсти в соответствии с пропорцией:
надо
соблюсти в соответствии с пропорцией:![]() .
.
4.
Сложив вектора ![]() и
и![]() в
соответствии с первым законом Кирхгофа,
получим:
в
соответствии с первым законом Кирхгофа,
получим:![]() .
.
5.
Угол ![]() определит
направление вектора напряжения
определит
направление вектора напряжения![]() ,
относительно тока
,
относительно тока![]() ,
величина вектора
,
величина вектора![]() определится
из соотношения
определится
из соотношения![]() .
.
6.
Геометрическим сложением определим ![]() ,
остается задаться конкретным масштабом,
приравняв
,
остается задаться конкретным масштабом,
приравняв![]() ,
и выбрать масштаб тока. Полученная
диаграмма с точностью до геометрических
построений дает ответы обо всех величинах
токов и напряжений и их относительных
фазах. Например, перпендикуляр из конца
вектора
,
и выбрать масштаб тока. Полученная
диаграмма с точностью до геометрических
построений дает ответы обо всех величинах
токов и напряжений и их относительных
фазах. Например, перпендикуляр из конца
вектора![]() на
направление тока
на
направление тока![]() даст
напряжение на катушке
даст
напряжение на катушке![]() .
Векторную диаграмму можно использовать
для проверки правильности алгебраических
расчетов. Например, угол
.
Векторную диаграмму можно использовать
для проверки правильности алгебраических
расчетов. Например, угол![]() между
током
между
током![]() и
входным напряжением
и
входным напряжением![]() должен
быть равен
должен
быть равен![]() .
.
12. Активная, реактивная и полная мощность в цепях синусоидальных токов. Мгновенное значение мощности. Измерение мощности.
Активная
- Это
мощность (для любых периодических
сигналов) определяется как среднее
значение мощности за период

График
рис. 4-9 полностью согласуется с
представлением о реактивных элементах,
которые не рассеивают энергии (P=0), а
только запасают ее и отдают обратно в
цепь. В те промежутки времени, когда ![]() -
реактивный элемент запасает энергию,
а когда
-
реактивный элемент запасает энергию,
а когда![]() отдает
энергию обратно. Этому колебанию энергии
соответствуетреактивная
мощность,
которую можно определить чисто
формально:
отдает
энергию обратно. Этому колебанию энергии
соответствуетреактивная
мощность,
которую можно определить чисто
формально:![]() .
.
Так
же в известной мере формально вводится
понятие полной,
или кажущейся, мощности,
как параметра отражающего предельные
возможности устройства по току и
напряжению
![]() .
Компл. Форма
.
Компл. Форма![]() .
.
Все три характеристики мощности имеют одинаковую размерность (ватт), но в технике получили разное наименование:
P - выражается в ваттах (ВТ),
Q - в вольт-амперах реактивных (ВАР),
S - в вольт-амперах (ВА).
