
- •Оглавление
- •1 .Электрическая цепь. Идеальные элементы электрических цепей и их свойства.
- •2 Схема электрической цепи. Топология. Матрицы соединений.
- •Уравнения Кирхгофа для мгновенных значений токов и напряжений.
- •II Закон Кирхгофа
- •I закон Кирхгофа
- •II закон Кирхгофа
- •5. Расчет простых цепей при постоянных токах и напряжениях. Эквивалентные преобразования пассивных и активных двухполюсников.
- •6 .Метод эквивалентного генератора.
- •7. Уравнения равновесия для обобщенной ветви.
- •8. Принцип наложения и его применение при анализе цепей.
- •9. Баланс мощностей и потенциальная диаграмма в цепях постоянного тока.
- •10.Синусоидальные токи и напряжения, из изображения векторами и комплексными числами.
- •11. Двухполюсники при синусоидальных токах и напряжениях. Расчет цепей при различных соединениях двухполюсников. Векторные диаграммы.
- •I. Последовательное соединение двухполюсников (рис. 4-14)
- •II. Параллельное соединение двухполюсников (рис. 4-16).
- •III. Смешанное соединение
- •12. Активная, реактивная и полная мощность в цепях синусоидальных токов. Мгновенное значение мощности. Измерение мощности.
- •Мгновенное значение мощности.
- •13. Комплексный метод расчета при последовательно-параллельном соединении двухполюсников. Построение векторной диаграммы.
- •14. Матричная запись уравнений Кирхгофа и Ома для сложных цепей.
- •15. Метод узловых потенциалов. Вывод уравнений.
- •16. Система уравнений по методу контурных токов.
- •17. Уравнения по методу сечений для обобщенной модели двухполюсника.
- •18. Резонанс напряжений, частотные характеристики.
- •19. Резонансные явления в сложных цепях без потерь. Частотные характеристики.
- •Частотные свойства параллельного контура
- •1.Параллельное соединение glc.
- •20. Расчет электрических цепей при несинусоидальных периодических токах и напряжениях.
- •21.Активная мощность при несинусоидальных периодических токах и напряжениях.
- •22.Измерения при несинусоидальных периодических токах и напряжениях приборами различных систем.
- •23.Уравнения четырехполюсников.
- •24.Эквивалентные схемы четырехполюсников.
- •25.Экспериментальное определение параметров четырехполюсников при синусоидальных токах и напряжениях.
- •26.Последовательное соединение четырехполюсников. Регулярность.
- •27.Параллельное соединение четырехполюсников. Регулярность.
- •28.Смешанное соединение четырехполюсников. Регулярность.
- •1. Одноэлементный (последовательный) четырехполюсник (рис. 8-14).
- •30.Понятие об активном четырехполюснике.
- •31.Характеристические параметры четырехполюсника. Затухание.
- •32 .Круговые диаграммы для простых схем. Порядок построения круговой диаграммы в общем случае.
6 .Метод эквивалентного генератора.
Докажем теорему:
любой активный двухполюсник можно заменить реальным источником напряжения с величиной ЭДС равной напряжению холостого хода и внутренним сопротивлением равным сопротивлению короткого замыкания.


Рис. 3-6
Доказывается
эта теорема показом эквивалентности
изображенных на рис. 3-6 схем с точки
зрения напряжения и тока нагрузки ![]() .
Действительно, включение двух одинаковых
идеальных источников с разнонаправленным
напряжением, в частности равным напряжению
холостого хода (при
.
Действительно, включение двух одинаковых
идеальных источников с разнонаправленным
напряжением, в частности равным напряжению
холостого хода (при![]() )
не изменит тока и напряжения нагрузки.
При этом
)
не изменит тока и напряжения нагрузки.
При этом![]() ,
поэтому активный двухполюсник вместе
со встречно направленным источником
,
поэтому активный двухполюсник вместе
со встречно направленным источником![]() можно
заменить пассивным двухполюсником.
Последний заменяется сопротивлением
короткого замыкания, названным так
потому, что в эксперименте оно может
быть получено, если измерить ток короткого
замыкания
можно
заменить пассивным двухполюсником.
Последний заменяется сопротивлением
короткого замыкания, названным так
потому, что в эксперименте оно может
быть получено, если измерить ток короткого
замыкания![]()
![]() .
.
Теорема доказана.
7. Уравнения равновесия для обобщенной ветви.
Для обобщенной ветви. (рис. 3-14).
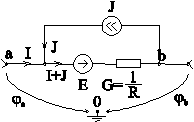
Рис. 3-14
По контуру: а-0-b-а
![]() ,
,
![]() .
.
8. Принцип наложения и его применение при анализе цепей.
Принцип наложения вытекает из физического принципа независимости действия сил в линейной системе. По этому принципу в схеме, где имеется два и более независимых источника, можно задачу анализа (поиск токов в ветвях и напряжений на элементах) искать отдельно для каждого источника, а результат алгебраически суммировать. При удалении какого-либо источника надо сохранять его внутреннее сопротивление. Это, практически, означает, что идеальный источник ЭДС закорачивается, а ветвь с идеальным источником тока разрывается.
Пример.
Определить токи в ветвях (рис. 3-17).
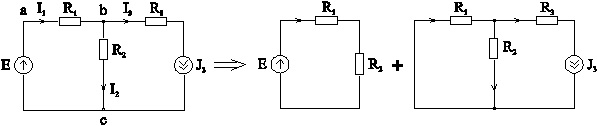
Рис. 3-17
Представляем схему, как результат “сложения” двух схем с источником ЭДС и с источником тока. Расчетные данные удобно свести в таблицу токов:
|
|
R1 |
R2 |
R3 |
|
Ток через резистор RK от действия источника Е1 |
|
|
О |
|
Ток через резистор RK от действия источника J3 |
|
|
J |
|
Ток через резистор RK |
|
|
J |
Примечания:
1. Знаки токов принимаются относительно одинаково выбранных для всех схем условных направлений.
2. Квадратичные формы (мощность, энергия) рассчитываются только для суммарных токов.
9. Баланс мощностей и потенциальная диаграмма в цепях постоянного тока.
Хорошей
проверкой результатов анализа цепи
является расчет баланса
мощности.
Как и для любой замкнутой системы ![]() .
Подсчитывается мощность, рассеиваемая
каждым резистором
.
Подсчитывается мощность, рассеиваемая
каждым резистором![]() и
каждым источником
и
каждым источником![]() .
Токи, конечно, берутся суммарные. Следует
обратить внимание, что для резисторов
.
Токи, конечно, берутся суммарные. Следует
обратить внимание, что для резисторов![]() всегда
положительны. Что касается мощности
источника, то если истинное напряжение
(а не ЭДС) и ток источника направлены
встречно, то
всегда
положительны. Что касается мощности
источника, то если истинное напряжение
(а не ЭДС) и ток источника направлены
встречно, то![]() ,
что означает отдачу энергии цепи. Если
,
что означает отдачу энергии цепи. Если![]() ,
то источник потребляет энергию. Для
определения величины и знака напряжения
на источнике тока необходимо составить
контурное уравнение по любому контуру,
содержащему источник тока:
,
то источник потребляет энергию. Для
определения величины и знака напряжения
на источнике тока необходимо составить
контурное уравнение по любому контуру,
содержащему источник тока:
![]() .
.
Контурное уравнение наглядно можно представить на потенциальной диаграмме. Для ее составления по оси абсцисс откладывают сопротивления соответствующих участков цепи, а по оси ординат - потенциалы в соответствующих точках. Составим диаграмму для контура а b с a предыдущего примера (рис. 3-18).
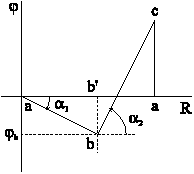
Рис. 3-18
Для
точки а примем потенциал ![]() .
Отрезок ab’ равен в выбранном масштабе
сопротивлению
.
Отрезок ab’ равен в выбранном масштабе
сопротивлению![]() .
Поскольку ток течет в направлении ab,
потенциал точки b меньше, чем точки a
.
Поскольку ток течет в направлении ab,
потенциал точки b меньше, чем точки a![]() .
.
Пусть ![]() ,
тогда потенциал точки c больше, чем b
,
тогда потенциал точки c больше, чем b![]() .
Величина отрезка са соответствует
.
Величина отрезка са соответствует![]() ;
;![]() ,
а
,
а![]() .
.
Изложенные в настоящей главе приемы расчета в различных сочетаниях, оставляя большие возможности для творчества, при известных навыках, позволяют быстро, без специальных вычислительных средств анализировать довольно сложные цепи.
