
- •Оглавление
- •1 .Электрическая цепь. Идеальные элементы электрических цепей и их свойства.
- •2 Схема электрической цепи. Топология. Матрицы соединений.
- •Уравнения Кирхгофа для мгновенных значений токов и напряжений.
- •II Закон Кирхгофа
- •I закон Кирхгофа
- •II закон Кирхгофа
- •5. Расчет простых цепей при постоянных токах и напряжениях. Эквивалентные преобразования пассивных и активных двухполюсников.
- •6 .Метод эквивалентного генератора.
- •7. Уравнения равновесия для обобщенной ветви.
- •8. Принцип наложения и его применение при анализе цепей.
- •9. Баланс мощностей и потенциальная диаграмма в цепях постоянного тока.
- •10.Синусоидальные токи и напряжения, из изображения векторами и комплексными числами.
- •11. Двухполюсники при синусоидальных токах и напряжениях. Расчет цепей при различных соединениях двухполюсников. Векторные диаграммы.
- •I. Последовательное соединение двухполюсников (рис. 4-14)
- •II. Параллельное соединение двухполюсников (рис. 4-16).
- •III. Смешанное соединение
- •12. Активная, реактивная и полная мощность в цепях синусоидальных токов. Мгновенное значение мощности. Измерение мощности.
- •Мгновенное значение мощности.
- •13. Комплексный метод расчета при последовательно-параллельном соединении двухполюсников. Построение векторной диаграммы.
- •14. Матричная запись уравнений Кирхгофа и Ома для сложных цепей.
- •15. Метод узловых потенциалов. Вывод уравнений.
- •16. Система уравнений по методу контурных токов.
- •17. Уравнения по методу сечений для обобщенной модели двухполюсника.
- •18. Резонанс напряжений, частотные характеристики.
- •19. Резонансные явления в сложных цепях без потерь. Частотные характеристики.
- •Частотные свойства параллельного контура
- •1.Параллельное соединение glc.
- •20. Расчет электрических цепей при несинусоидальных периодических токах и напряжениях.
- •21.Активная мощность при несинусоидальных периодических токах и напряжениях.
- •22.Измерения при несинусоидальных периодических токах и напряжениях приборами различных систем.
- •23.Уравнения четырехполюсников.
- •24.Эквивалентные схемы четырехполюсников.
- •25.Экспериментальное определение параметров четырехполюсников при синусоидальных токах и напряжениях.
- •26.Последовательное соединение четырехполюсников. Регулярность.
- •27.Параллельное соединение четырехполюсников. Регулярность.
- •28.Смешанное соединение четырехполюсников. Регулярность.
- •1. Одноэлементный (последовательный) четырехполюсник (рис. 8-14).
- •30.Понятие об активном четырехполюснике.
- •31.Характеристические параметры четырехполюсника. Затухание.
- •32 .Круговые диаграммы для простых схем. Порядок построения круговой диаграммы в общем случае.
22.Измерения при несинусоидальных периодических токах и напряжениях приборами различных систем.
Из формулы:
 .
.
следует, что для измерения мощности требуется иметь прибор, перемножающий две функции времени и вычисляющий среднее значение (постоянную составляющую) такой функцию.
При моделировании электрических цепей на ЭВМ в программах типа Electronics Workbench имеется элемент-перемножитель. При его использовании совместно с вольтметром (Д.С.), регистрирующим среднее значение напряжения можно получить требуемое преобразование. Возможная “схема” включения такого прибора приведена на рис. 4-10.

Рис. 4-10
Для измерения мощности в реальных цепях применяют электродинамические ваттметры. Они состоят из двух магнитно-связанных катушек, одна из которых может вращаться вокруг оси. С подвижной катушкой связана стрелка, показывающая на шкале угол ее отклонения от нулевого положения, которое поддерживается специальной пружинкой.

Рис. 4-11
Противодействующий
момент пружинки по закону Гука
пропорционален углу отклонения стрелки
- ![]() .
.
![]()
Вращающий момент определяется изменением энергии запасенной системой при пропускании токов через катушки при повороте подвижной катушки
![]() .
.
Равновесие
достигается при ![]() .
.
![]() .
.
Энергия, запасенная системой двух катушек:
![]() .
.
Первые
два слагаемых от угла ![]() не
зависят
не
зависят
 .
.
Т.к. механическая инерционность системы приведет к тому, что угол отклонения стрелки будет пропорционален среднему значению момента.
Таким
образом, если через одну из катушек
пропускать ток пропорциональный току
приемника, а через другую - пропорциональный
его напряжению, получим (в предположении ![]() ),
что угол
),
что угол![]() будет
пропорционален активной мощности
будет
пропорционален активной мощности
![]() .
.
На рис. 4-11 показана схема включения ваттметра. Точками (или звездочками) отмечены зажимы, которые следует объединить, т.к. направление вращающегося момента зависит от согласования направлений тока и напряжения.
23.Уравнения четырехполюсников.
Электротехническое устройство, служащее для передачи энергии (сигналов) и имеющие по два входных и выходных зажима, называется четырехполюсником.
Если внутри четырехполюсника нет источников энергии или они взаимно компенсируют друг друга, то такой четырехполюсник называют пассивным (рис. 8-1: а - идеальный трансформатор; б - частотный фильтр; в - мостовая схема).

Рис. 8-1
Рассмотрим свойства четырехполюсников в установившемся режиме при периодических синусоидальных токах и напряжениях. Это позволит в дальнейшем применить полученные результаты для анализа цепей при других формах сигналов.
Для
анализа свойств четырехполюсника
установим зависимость между входным
напряжением ![]() и
токами
и
токами![]() и
входными
и
входными![]() и
и![]() (рис.
8-2, где П - пассивная схема).
(рис.
8-2, где П - пассивная схема).

Рис. 8-2
При
выборе направлений напряжений и токов,
указанных на рисунке, энергия передается
от входа (клемма a-b) к сопротивлению
нагрузки ![]() (клеммы
c-d).
(клеммы
c-d).
Составим
уравнение цепи методом контурных токов.
В первый контур включим входные зажимы,
во второй контур включим сопротивление
нагрузки ![]() .
.
![]()
![]()
- - - - - - - - - - - - - - - - - - - - - -
![]() .
.
Обозначим ![]() ,
где
,
где![]() -
часть сопротивления второго контура,
входящая в состав четырехполюсника.
-
часть сопротивления второго контура,
входящая в состав четырехполюсника.
Учитывая,
что ![]() :
:
![]()
![]()
- - - - - - - - - - - - - - - - - - -
![]() .
.
Все остальные уравнения содержат в правой части нули, что соответствует пассивному четырехполюснику.
Решение системы уравнений:
![]() ;
;
![]() .
.
Отношения ![]() ,
,![]() имеют
размерность проводимости.
имеют
размерность проводимости.
Обозначим
![]() ;
; ![]() ;
;![]() ;
;![]() ,
,
тогда уравнения четырехполюсника принимают вид:
![]() ;
;
![]() .
.
В матричной форме:
 ,
,
или
![]() .
.
Для
линейных уравнений, соответствующих
линейным цепям ![]() ,
поэтому
,
поэтому![]() .
.
Указанные
коэффициенты называются Y-параметрами,
а матрица Y-матрицей
четырехполюсника. Как видно из записи
уравнений четырехполюсников в Y-параметрах
с учетом уравнения ![]() ,
пассивный четырехполюсник характеризуется
тремя независимыми параметрами.
Физический смысл Y-параметров можно
определить по режимам короткого замыкания
на выходе
,
пассивный четырехполюсник характеризуется
тремя независимыми параметрами.
Физический смысл Y-параметров можно
определить по режимам короткого замыкания
на выходе![]() и
на входе
и
на входе![]() .
.
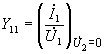 -
входная проводимость при коротком
замыкании на выходе.
-
входная проводимость при коротком
замыкании на выходе.
 -
передаточная (взаимная) проводимость
при коротком замыкании на входе.
-
передаточная (взаимная) проводимость
при коротком замыкании на входе.
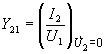 -
передаточная проводимость при коротком
замыкании на выходе.
-
передаточная проводимость при коротком
замыкании на выходе.
 -
выходная проводимость при коротком
замыкании на входе.
-
выходная проводимость при коротком
замыкании на входе.
Решим систему уравнений относительно напряжений:
![]() ,
,
где
 .
.
Или в развернутом виде
![]() ,
,
![]() .
.
Два из четырех параметров связаны между собой:
![]() .
.
Физический
смысл Z-параметров четырехполюсника
можно определить по режимам холостого
хода на выходе (![]() )
и на входе (
)
и на входе (![]() ).
).
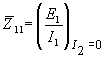 -
входное сопротивление в режиме холостого
хода на выходе.
-
входное сопротивление в режиме холостого
хода на выходе.
 -
передаточное (взаимное) сопротивление
в режиме холостого хода на входе.
-
передаточное (взаимное) сопротивление
в режиме холостого хода на входе.
 -
передаточное сопротивление в режиме
холостого хода на выходе.
-
передаточное сопротивление в режиме
холостого хода на выходе.
 -
выходное сопротивление зажимов 22’ в
режиме холостого хода на входе.
-
выходное сопротивление зажимов 22’ в
режиме холостого хода на входе.
Во многих практических случаях удобно, когда система уравнений решена относительно выходных напряжений и тока:
![]() ,
,
![]() .
.
Параметры A, B, C, D в общем случае комплексные. Их можно выразить, например, через Z-параметры.
Решая
второе уравнение Z-параметров относительно
тока ![]() ,
получим:
,
получим:
![]() .
.
Сопоставив со вторым уравнением в A-параметрах, получаем:
![]() ;
; ![]()
Подставим ![]() в
первое уравнение в Z-параметрах:
в
первое уравнение в Z-параметрах:
![]() .
.
Таким образом,
![]() ;
; ![]() .
.
Нетрудно убедиться, что AD-BC=1.
Физический смысл А-параметров:
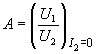 -
передаточное отношение напряжений в
режиме холостого хода на выходе.
-
передаточное отношение напряжений в
режиме холостого хода на выходе.
 -
передаточное сопротивление при коротком
замыкании на выходе.
-
передаточное сопротивление при коротком
замыкании на выходе.
 -
передаточная проводимость в режиме
холостого хода на выходе.
-
передаточная проводимость в режиме
холостого хода на выходе.
 -
передаточное отношение токов при
коротком замыкании на выходе.
-
передаточное отношение токов при
коротком замыкании на выходе.
При обратном питании с учетом изменения знаков токов получим:
 .
.
При этом сохраняется соотношение
AD-BC=1
Для формирования уравнений при смешанном соединении четырехполюсников применяются еще два уравнения в H-параметрах и G-параметрах:
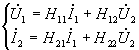 ,
,
![]() ,
,
 ,
,
![]() .
.
Физический смысл предлагаем установить читателю.
