20. Расчет электрических цепей при несинусоидальных периодических токах и напряжениях.

В большинстве устройств электроники, радиотехники, автоматики, вычислительной техники токи и напряжения имеют отличную от синусоидальной форму, оставаясь периодическими функциями времени. Расчет цепей при несинусоидальных периодических возмущающих воздействиях в курсе электротехники составляет самостоятельный раздел, не зависимо от того, чем вызвана несинусоидальность. Причиной несинусоидальности могут быть паразитные явления, протекающие в электротехнических установках: несимметричность генераторов, нелинейность характеристик элементов и т.д.

Широко применяются устройства, в которых несинусоидальность возмущающих воздействий создается преднамеренно и несет определенную информацию: вычислительные устройства, системы связи и т.п.

Метод расчета электрических цепей при несинусоидальных периодических токах и напряжениях основан на разложении кривой в гармонический ряд Фурье и применении принципа наложения.

Расчет цепей содержит следующие этапы:

1. Разложение заданных ЭДС или токов источников на гармонические составляющие.

2. Расчет токов и напряжений для каждой составляющей отдельно (на основе принципа наложения).

3. Квадратичное суммирование решений для каждой составляющей.

Обычно ряды Фурье сходятся довольно быстро и в зависимости от требуемой точности решения задачи с учетом характера цепи ограничиваются определенным количеством членов разложения. Таким образом, расчет сводится к решению стольких однотипных задач, сколькими гармониками ограничиваются. При этом учитывается, что для различных частот сопротивления элементов схемы неодинаковы.

Сопротивление катушки индуктивности для постоянной составляющей ; сопротивление дляk-й гармоники в к раз больше, чем для основной:

.

Конденсатор не пропускает постоянную составляющую (); дляk-й гармоники сопротивления емкости в к раз меньше, чем для основной:

 .

Активное сопротивление также зависит от частоты, возрастая с ее увеличением из-за поверхностного эффекта. Однако для цепей, рассматриваемых в электротехнике, зависимость обычно не учитывают, считая .

Вследствие зависимости реактивных сопротивлений от частоты токи и падения напряжений в цепях, содержащих емкости, имеют больший коэффициент гармоник, чем ЭДС генератора. Иными словами, отклонение от синусоиды в емкостных цепях усиливается.

В индуктивных цепях происходит обратное явление, т.е. индуктивность подавляет проявление высших гармоник.

21.Активная мощность при несинусоидальных периодических токах и напряжениях.

Общее правило определения активной мощности P:

.

После перемножения под интегралом получаем сумму произведений двух видов: и.

Интеграл от слагаемых первого вида:

.

Интегралы от слагаемых второго вида обращаются в ноль, так как они представляют собой интегралы от синусоидальных функций за целое число периодов.

.

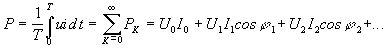Активная мощность при периодических несинусоидальных токах и напряжениях равна сумме активных мощностей постоянной и всех гармонических составляющих тока и напряжения.

Понятие коэффициента мощности при несинусоидальных токах и напряжения не совпадает с понятием :

.

Появление высших гармоник в цепях, содержащих реактивные сопротивления, приводит к снижению коэффициента мощности, только при чисто резистивной цепи.

 - угол сдвига фаз между эквивалентными синусоидами тока и напряжения, действующие значения которых такие же, как у несинусоидальных.