
- •Оглавление
- •1 .Электрическая цепь. Идеальные элементы электрических цепей и их свойства.
- •2 Схема электрической цепи. Топология. Матрицы соединений.
- •Уравнения Кирхгофа для мгновенных значений токов и напряжений.
- •II Закон Кирхгофа
- •I закон Кирхгофа
- •II закон Кирхгофа
- •5. Расчет простых цепей при постоянных токах и напряжениях. Эквивалентные преобразования пассивных и активных двухполюсников.
- •6 .Метод эквивалентного генератора.
- •7. Уравнения равновесия для обобщенной ветви.
- •8. Принцип наложения и его применение при анализе цепей.
- •9. Баланс мощностей и потенциальная диаграмма в цепях постоянного тока.
- •10.Синусоидальные токи и напряжения, из изображения векторами и комплексными числами.
- •11. Двухполюсники при синусоидальных токах и напряжениях. Расчет цепей при различных соединениях двухполюсников. Векторные диаграммы.
- •I. Последовательное соединение двухполюсников (рис. 4-14)
- •II. Параллельное соединение двухполюсников (рис. 4-16).
- •III. Смешанное соединение
- •12. Активная, реактивная и полная мощность в цепях синусоидальных токов. Мгновенное значение мощности. Измерение мощности.
- •Мгновенное значение мощности.
- •13. Комплексный метод расчета при последовательно-параллельном соединении двухполюсников. Построение векторной диаграммы.
- •14. Матричная запись уравнений Кирхгофа и Ома для сложных цепей.
- •15. Метод узловых потенциалов. Вывод уравнений.
- •16. Система уравнений по методу контурных токов.
- •17. Уравнения по методу сечений для обобщенной модели двухполюсника.
- •18. Резонанс напряжений, частотные характеристики.
- •19. Резонансные явления в сложных цепях без потерь. Частотные характеристики.
- •Частотные свойства параллельного контура
- •1.Параллельное соединение glc.
- •20. Расчет электрических цепей при несинусоидальных периодических токах и напряжениях.
- •21.Активная мощность при несинусоидальных периодических токах и напряжениях.
- •22.Измерения при несинусоидальных периодических токах и напряжениях приборами различных систем.
- •23.Уравнения четырехполюсников.
- •24.Эквивалентные схемы четырехполюсников.
- •25.Экспериментальное определение параметров четырехполюсников при синусоидальных токах и напряжениях.
- •26.Последовательное соединение четырехполюсников. Регулярность.
- •27.Параллельное соединение четырехполюсников. Регулярность.
- •28.Смешанное соединение четырехполюсников. Регулярность.
- •1. Одноэлементный (последовательный) четырехполюсник (рис. 8-14).
- •30.Понятие об активном четырехполюснике.
- •31.Характеристические параметры четырехполюсника. Затухание.
- •32 .Круговые диаграммы для простых схем. Порядок построения круговой диаграммы в общем случае.
19. Резонансные явления в сложных цепях без потерь. Частотные характеристики.
Рассмотрим двухполюсник, содержащий параллельно соединенные RLC (GLC) (рис. 6-10,а). Условие резонанса:
![]() или
или ![]() .
.
Значение параметров при резонансе:
![]() ;
; ![]() .
.
Векторная диаграмма цепи показана на рис. 6-10,б.
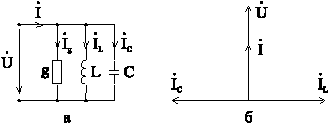
Рис. 6-10
Поскольку в данном случае равны и противоположны по фазе векторы токов, резонанс в параллельной цепи называют резонансом токов.
При резонансе реактивная проводимость двухполюсника равна нулю и полная проводимость минимальна, поэтому полный ток при резонансе минимален.
Величина
![]() называется волновой
проводимостью.
называется волновой
проводимостью.
Если ![]() ,
то ток
,
то ток![]() .
.
Отношение
![]() ,
,
определяющее
степень превышения тока в реактивных
элементах суммарного тока при резонансе
- добротность
контура. ![]() -затухание
контура.
-затухание
контура.
Энергетические
процессы в параллельном контуре
аналогичны процессам в последовательной
RLC-цепи. В любой момент времени ![]() ,
т.е. энергия переходит из катушки в
конденсатор и обратно. Источник
компенсирует потери энергии в проводимости
G.
,
т.е. энергия переходит из катушки в
конденсатор и обратно. Источник
компенсирует потери энергии в проводимости
G.
Частотные свойства параллельного контура
При построении частотных характеристик параллельной цепи наглядно прослеживается принцип дуальности цепей.
1.Параллельное соединение glc.
Величина
тока ![]() .
Характеристики в этом случае дуальны
последовательному соединению RLC при
постоянстве приложенного напряжения
.
Характеристики в этом случае дуальны
последовательному соединению RLC при
постоянстве приложенного напряжения![]() .
.
![]() ;
; 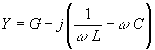 ;
;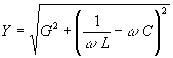 .
.
Напряжение двухполюсника (действующее значение)
 .
.
Токи элементов
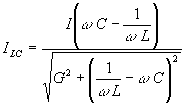 ;
; 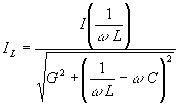 ;
;
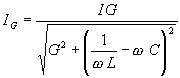 ;
; 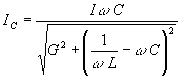 .
.
При построении АЧХ следует учитывать, что для резонанса:
![]() ;
; ![]() ;
;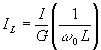 ;
;![]() ;
;
![]() ;
; ![]() ;
;![]() ;
;
![]() ;
;
при ![]()
![]() ;
; ![]() ;
;![]() ;
;
при ![]()
![]() ;
; ![]() ;
;![]() .
.
График характеристик цепи представлен на рис. 6-10.
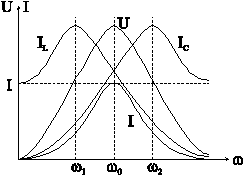
Рис. 6-10
2.
Параллельное соединение GLC,
приложенное напряжение постоянно по
величине ![]() .
Частотные характеристики дуальны
характеристикам цепи с последовательным
соединением RLC при
.
Частотные характеристики дуальны
характеристикам цепи с последовательным
соединением RLC при![]() .
АЧХ элементов и двухполюсника соответствуют
зависимостям проводимостей элементов
от частоты (рис. 6-11,а).
.
АЧХ элементов и двухполюсника соответствуют
зависимостям проводимостей элементов
от частоты (рис. 6-11,а).
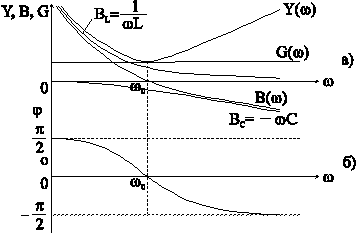
Рис. 6-11
Реактивная проводимость, равная
![]() ,
,
имеет
два полюса ![]() и
и![]() и
один ноль
и
один ноль![]() .
Реактивная проводимость с увеличением
частоты уменьшается:
.
Реактивная проводимость с увеличением
частоты уменьшается:
![]() .
.
При
переходе частоты через точку резонанса
изменяется характер проводимости:
при ![]() проводимость
имеет индуктивный характер
проводимость
имеет индуктивный характер![]() ;
при
;
при![]() проводимость
становится емкостной
проводимость
становится емкостной![]() .
ФЧХ представлена на рис. 6-11,б.
.
ФЧХ представлена на рис. 6-11,б.
Найдем характеристики сопротивления параллельно соединенных R, L, C. Реактивное сопротивление цепи
![]() .
.
Если G=0, то
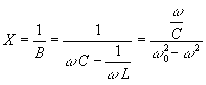 .
.
График
зависимостей ![]() и
и![]() представлены
на рис. 6-12.
представлены
на рис. 6-12.
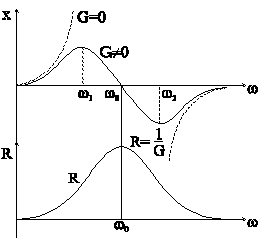
Рис. 6-12
Заметим,
что при ![]() ,
т.е. с увеличением частоты сопротивление
в цепях без потерь всегда возрастает.
В момент перехода частоты через точку
резонанса сопротивление становится
бесконечным и изменяет свой характер
от индуктивного к емкостному (пунктирная
линия). При
,
т.е. с увеличением частоты сопротивление
в цепях без потерь всегда возрастает.
В момент перехода частоты через точку
резонанса сопротивление становится
бесконечным и изменяет свой характер
от индуктивного к емкостному (пунктирная
линия). При![]() характер
зависимостиХ от
характер
зависимостиХ от ![]() показан
сплошной линией. Прохождение
показан
сплошной линией. Прохождение![]() через
ноль не означает, что сопротивление
всей цепи равно нулю, так как активное
сопротивление, зависящее в этом случае
от частоты, имеет максимум в момент
резонанса:
через
ноль не означает, что сопротивление
всей цепи равно нулю, так как активное
сопротивление, зависящее в этом случае
от частоты, имеет максимум в момент
резонанса:
![]() .
.
Влияние
величины активной проводимости G на
характер зависимостей показано векторными
диаграммами для различных соотношений ![]() ;
;![]() и
G (рис. 6-13,а,б,в).
и
G (рис. 6-13,а,б,в).
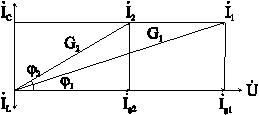
а)
![]() ;
; ![]() ;
;![]() .
.
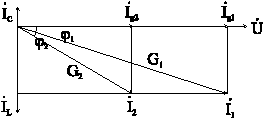
б)
![]() ;
; ![]() ;
;![]() .
.
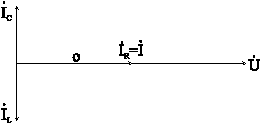
в)
![]() ;
; ![]() .
.
Рис. 6-13
Влияние G, L, C на АЧХ и ФЧХ исследуется по аналитическим зависимостям.
Поскольку
в цепях без потерь угол сдвига фаз между
током и напряжением может быть только ![]() ,
а в то же время при резонансе
,
а в то же время при резонансе![]() ,
так как в момент резонанса
,
так как в момент резонанса![]() скачком
меняет свой знак (рис. 6-16).
скачком
меняет свой знак (рис. 6-16).
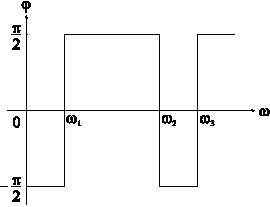
Рис. 6-16
Точками
резонанса также будут значения
частот ![]() и
и![]() .
.
Далее,
поскольку, ![]() ,
неравенство усиливается, то справедливы
соотношения
,
неравенство усиливается, то справедливы
соотношения
![]() .
.
Для
любой цепи без потерь первой резонансной
частотой является ![]() и
последней
и
последней![]() .
Однако, в зависимости от того, будет ли
при этих частотах ноль или полюс функции,
можно представить четыре разновидности
характеристик (рис. 6-17).
.
Однако, в зависимости от того, будет ли
при этих частотах ноль или полюс функции,
можно представить четыре разновидности
характеристик (рис. 6-17).
Если в двухполюснике существует путь, проходящий только по индуктивности, то зависимость
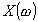 начинается
с нуля (рис. 6-17,а,в).
начинается
с нуля (рис. 6-17,а,в).При отсутствии такого пути
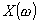 начинается
с полюса (рис. 6-17,б,г).
начинается
с полюса (рис. 6-17,б,г).Если в двухполюснике существует путь, проходящий только по емкостям, то зависимость
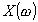 заканчивается
нулем (рис. 6-17,а,б).
заканчивается
нулем (рис. 6-17,а,б).При отсутствии такого пути частотная характеристика заканчивается полюсом (рис. 6-17,в,г).
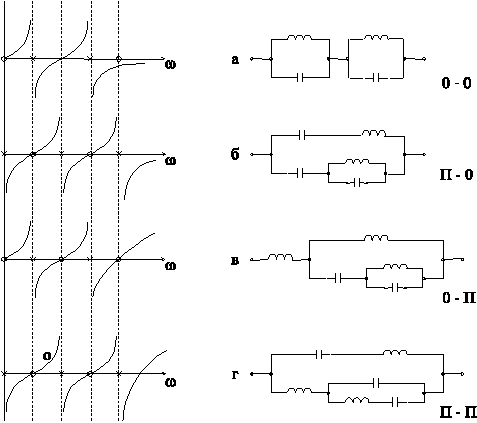
Рис. 6-17
