18. Резонанс напряжений, частотные характеристики.

Рассмотрим двухполюсники, содержащие L и C. Различные сочетания индуктивностей и емкостей в цепи при заданной частоте, либо изменение частоты при заданной схеме могут привести к тому, что входная проводимость или входное сопротивление двухполюсника будут иметь чисто активный характер. При этом напряжение и ток на входе двухполюсника совпадают по фазе. Такое явление называют резонансом.

Основное определение резонанса: (на входе двухполюсника).

Рассмотрим некоторые характеристики цепи при резонансе. Для последовательной RLC-цепи (рис. 6-1) ток и сдвиг по фазе между током и напряжением равны:

;

.

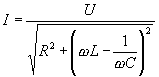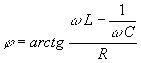Рис. 6-1

Резонанс в цепи возникает при выполнении условий

 или .

Частота в этом случае называется резонансной или собственной, а ток имеет максимальное значение:

.

Векторная диаграмма цепи при резонансе представлена на рис. 6-2.

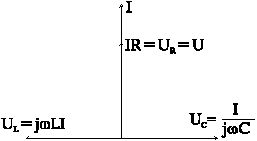
Рис 6-2

Векторы иравны по величине и противоположно направлены. Поэтому резонанс в последовательной RLC-цепи называют также резонансом напряжений.

Условие резонанса можно записать в другой форме

.

Эта формула удобна для анализа цепи, когда резонанс достигается изменением одной из трех величин: ,L или C, т.е. при постоянстве двух величин изменяемая величина должна получить значения:

; ;;

 - волновое сопротивление.

Действующее значение напряжения на реактивных элементах при резонансе

может существенно превышать питающее напряжение в зависимости от добротности контура Q:

; .

Величина, обратная добротности - затухание контура. Для выяснения физической сущности явления резонанса рассмотрим мгновенные значения мощностей на элементахL, R, C.

;

;

.

Поскольку , то. Это значит, что происходит обмен энергией между магнитным полем катушки и электрическим полем конденсатора. Источник в этом случае расходует энергию только на потери в активном сопротивлении. Суммарная энергия магнитного и электрического полей:

,

учитывая, что

,

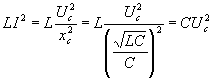получаем

,

т.е. суммарная энергия полей конденсатора и катушки индуктивности остается постоянной.

1. Последовательная RLC-цепочка при условии (рис. 6-3).

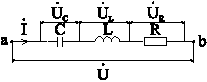
Рис. 6-3

Напряжение двухполюсника , где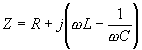, или в действующих значениях, где.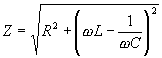

Для каждого элемента частотные характеристики представляют собой зависимости модуля сопротивления элемента от частоты. Для АЧХ двухполюсникахарактер зависимости совпадает с зависимостью модуля сопротивления двухполюсника, т.е..

АЧХ элемента и всего двухполюсника представлены на рис. 6-4.

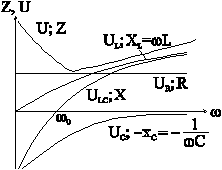
Рис 6-4

Реактивное сопротивление двухполюсника изменяется отдо, проходя через 0 в точке. Используя понятие нуля и полюса системной функции, заметим, что у функциидва полюса:ии один ноль. Характерное свойство функциисостоит в том, что, так как при увеличении частоты растут (алгебраически) оба слагаемых. ФЧХ получаем из выражения:

,

т.е., считая , имеем

.

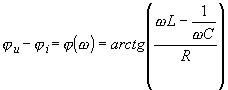Зависимость показана на рис. 6-5. Если(при), то цепь имеет емкостный характер, если(при) - индуктивный характер.

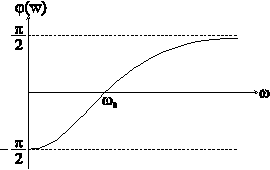
Рис. 6-5

2. Последовательная RLC-цепочка; приложенное напряжение постоянно по величине .

Ток в цепи

;

; ;

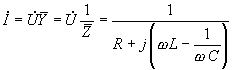или для действующих значений:

; ;

; ;

.

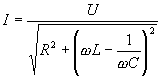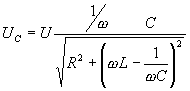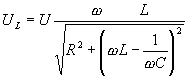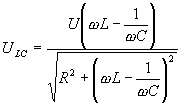При построении графиков частотных зависимостей учитывается, что при резонансе X=0, тогда

; ;;

; .

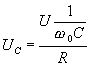При ;;;;.

При ;;;;.

Зависимость тока и напряжений элементов от частоты приведены на рис. 6-6.

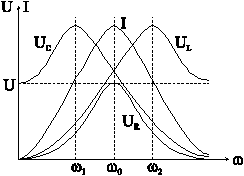
Рис. 6-6

Рассмотрим влияние частоты на проводимость данной цепи

.

Предположим (цепь без потерь), тогда

.

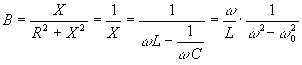Функция имеет два нуляии один полюс. Производная, т.е. в цепях без потерь проводимость всегда убывает, что соответствует пунктирной кривой рис. 6-7.

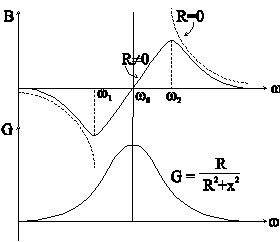
Рис. 6-7

В реальной цепи сопротивление 

.

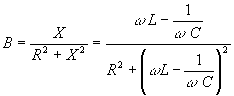Полученная зависимость предоставлена на рис. 6-7 сплошной линией. Значения частот иможно найти из условия

.

Решение уравнений приводит к соотношению:

.

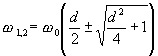Откуда экстремальные значения , а, где- затухание контура.

Рассмотрим влияние параметров двухполюсника на частотные характеристики цепи. На рис. 6-8 приведены векторные диаграммы RLC-цепи при (а);(б) и(в). При неизмененныхиуменьшение R приводит к увеличению сдвига фаз между током и напряжением всей цепи, при этом сохраняется характер двухполюсника. В точке резонанса величина R не влияет на фазу.

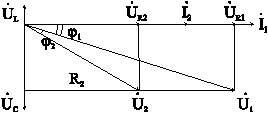
а)

; ;.

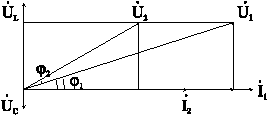
б)

; ;.

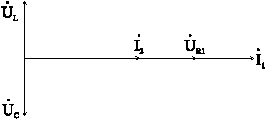
в)

.

Рис. 6-8

Влияние параметров цепи на частотные характеристики выводится из зависимостей ;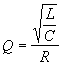. Откуда видно, чтоR не влияет на , увеличение R уменьшает добротность, т.е. кривыеи, приведенные на рис. 6-6, будут более пологими. Частота, при котороймаксимальна, уменьшается, а, соответствующая, увеличивается.

Изменение C влияет на резонансную частоту: увеличение C в n раз уменьшает и добротностьQ в раз и наоборот.

Изменение L аналогично влияет на резонансную частоту и противоположно на добротность. Если, например, необходимо увеличить , не уменьшая добротности, то нужно уменьшить величинуL. При уменьшении для сохранения добротности не ниже заданной величины увеличиваютL. ФЧХ последовательной RLC-цепи при уменьшении R становится более крутой и при R=0 вырождается в ломаную прямую (рис. 6-9). Изменение L или С в соответствии с формулой смещает и изменяет крутизну кривой. При уменьшенииL смещается вправо и кривая становится более пологой, при уменьшенииС кривая смещается в ту же сторону, но становится более крутой.

Рис. 6-9