
- •1. Роль математики и информационных технологий в гуманитарных науках. Количественные методы в языкознании.
- •2. Информация и информационные процессы.
- •2. Информация и информационные процессы
- •3. Основные понятия аксиоматической теории. Аксиомы, пастулаты, теоремы.
- •4. Аксиоматический метод, его сущность. Примеры применения аксиоматического метода в языкознании.
- •5. Алгоритмы и их свойства.
- •6. Классификация языков программирования. Компоненты системы программирования.
- •7. Базы данных Access: функции и назначение. Режим таблицы. Типы данных и сортировка
- •8. Базы данных Access. Понятие формы, режимы работы с формой. Формирование отчетов и запросов в Access.
- •9. Создание презентаций средствами PowerPoint.
- •10. Создание презентаций средствами Microsoft Office PowerPoint
- •11. Интернет. История создания и принцип функционирования.
- •12. Поиск информации образовательного назначения в интернет.
- •13. Классификация программного обеспечения.
- •14. Технологии обработки текстовой информации.
- •15. Технологии создания и обработки компьютерной графики.
- •16. Технология хранения, поиска и сортировки информации.
- •17. Технология обработки числовой информации
- •18. Архиваторы и антивирусные пакеты.
- •19. Модель, оригинал, структурная модель. Математические методы моделирования
- •20. Числа, фигуры, множества как примеры математических моделей. Компьютерное моделирование.
- •21. Понятие множества. Способы задания множеств. Чёткие и нечёткие, конечные и бесконечные множества
- •22. Отношения между множествами. Основные операции над множествами.
- •23. Разбиение множества на классы. Классификация.
- •24. Численность конечных множеств. Число элементов объединения и разности двух конечных множеств.
- •25. Бинарные отношения, свойства отношений. Отношения эквивалентности, порядка и толерантности.
- •26. Комбинаторика и лингвистические множества. Понятие факториала. Комбинаторика и лингвистические множества.
- •27. Размещения, размещения с повторениями
- •28. Перестановки, перестановки с повторениями. Сочетания.
- •29. Понятие события, случайные события. Понятие вероятности, вероятность элементарного лингвистического события.
- •30. Классическое определение вероятности.
- •31. Статистическое определение вероятности. Выборочное частотное описание текста.
- •32. Зависимые лингвистические события и условные вероятности.
24. Численность конечных множеств. Число элементов объединения и разности двух конечных множеств.
Конечное множество — множество, количество элементов которого конечно, то есть, существует неотрицательное целое число k, равное количеству элементов этого множества. Число элементов конечного множества является натуральным числом и называется мощностью множества. Возьмем множество A, тогда мощность этого множества будем обозначать как n(A).
Объединение
Объединением двух множеств A и B называется множество A B, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств A или B. Операция ИЛИ.
Пересечением множеств A и B называется множество A B, которое состоит из тех и только тех элементов, которые принадлежат как множеству A, так и множеству B. Операция И.
Тогда число элементов объединения двух конечных множеств вычисляется по формуле:
n(А ∪ В) = n(А) + n(В) - n(А ∩ В).
Иными словами, число элементов объединения двух конечных множеств равно разности суммы их численности и числа повторяющихся (пересекающихся) элементов.


A А ∩ В B
Разность
Разностью множеств A и B называется множество A \ B, которое состоит из тех и только тех элементов, которые принадлежат множеству A, но не принадлежат множеству B.
A \ B = { x A; x B}
Число элементов разности двух конечных множеств вычисляется по формуле:
n(А \ В) = n(А) - n(А ∩ В).
Иначе говоря, число элементов разности двух конечных множеств (A \ B) равняется разности численности множества A и числа повторяющихся (пересекающихся) элементов.
25. Бинарные отношения, свойства отношений. Отношения эквивалентности, порядка и толерантности.
|
Бинарным
отношением (англ. binary
relation) |
Часто
используют инфиксную форму записи: ![]() .
.
Если
отношение определено на множестве ![]() ,
то возможно следующее определение:
,
то возможно следующее определение:
|
Определение: |
|
Бинарным (или двуместным) отношением |
Примерами
множеств с введёнными на них бинарными
отношениями являются графы и
частично упорядоченные множества.





Для ![]() определены
свойства:
определены
свойства:
Рефлексивность (англ. reflexivity):
 ;
;
Отношение R на множестве Х называется рефлексивным, если о каждом элементе множества Х можно сказать, что он находится в отношении R с самим собой: хRх. Если отношение рефлексивно, то в каждой вершине графа имеется петля. И обратно, граф, каждая вершина которого содержит петлю, представляет собой граф рефлексивного отношения.
Примерами рефлексивных отношений являются и отношение «кратно» на множестве натуральных чисел (каждое число кратно самому себе), и отношение подобия треугольников (каждый треугольник подобен самому себе), и отношение «равенства» (каждое число равно самому себе) и др.
Антирефлексивность (англ. irreflexivity):
 ;
;
Отношение R на
множестве Х называется антирефлексивным,
если для любого элемента из множества Х всегда
ложно хRх:![]()
![]() .
.
Симметричность (англ. symmetry):
 ;
;
Отношение R на
множестве Х называется симметричным, если
выполняется условие: из того, что
элемент х находится
в отношении с элементом y,
следует, что и элемент y находится
в отношении R с
элементом х: xRy![]() yRx
.
yRx
.
Примерами симметричных отношений могут быть следующие: отношение «параллельности» отрезков, отношение «перпендикулярности» отрезков, отношение «равенства» отрезков, отношение подобия треугольников, отношение «равенства» дробей и др.
Антисимметричность (англ. antisymmetry):
 ;
;
Отношение R называют антисимметричным,
если для любых элементов х и y из
истинности xRy следует
ложность yRx:
: xRy![]() yRx.
yRx.
Транзитивность (англ. transitivity):
 ;
;
Отношение
R на множестве Х называют транзитивным, если
из того, что элемент х находится
в отношении R с
элементом y,а
элемент y находится
в отношении R с
элементом z,
следует, что элемент х находится
в отношении R с
элементом z: xRy и yRz![]() xRz.
xRz.
Свойством
транзитивности обладает и отношение
«длиннее» на множестве отрезков: если
отрезок а длиннее
отрезка b,
отрезок b длиннее
отрезка с,
то отрезок а длиннее
отрезка с. Отношение
«равенства» на множестве отрезков также
обладает свойством транзитивности: (а=b,
b=с)![]() (а=с).
(а=с).
Связность (англ. connectivity):
 ;
;
Отношение R на
множестве Х называется связанным, если
для любых элементов х и y из
данного множества выполняется условие:
если х и y различны,
то либо х находится
в отношении R с
элементом y,
либо элемент y находится
в отношении R с
элементом х.
С помощью символов это определение можно
записать так: x![]() y
y![]() xRy или yRx.
xRy или yRx.
Например, свойством связанности обладает отношение «больше» для натуральных чисел: для любых различных чисел х и y можно утверждать, либо x>y, либо y>x.
Ассимметричность (англ. assymetric relation):
 .
.
Выделяются следующие виды отношений:
квазипорядка (англ. quasiorder) — рефлексивное транзитивное;
эквивалентности (англ. equivalence) — рефлексивное симметричное транзитивное;
Отношение R на множестве Х называется отношением эквивалентности, если оно одновременно обладает свойством рефлексивности, симметричности и транзитивности.
Примерами отношений эквивалентности могут служить: отношения равенства геометрических фигур, отношение параллельности прямых (при условии, что совпадающие прямые считаются параллельными).
В
рассмотренном выше отношении «равенства
дробей», множество Х разбилось
на три подмножества: {![]() ;
; ![]() ;
;![]() },
{
},
{![]() ;
; ![]() }, {
}, {![]() }.
Эти подмножества не пересекаются, а их
объединение совпадает с множествомХ,
т.е. имеем разбиение множества на классы.
}.
Эти подмножества не пересекаются, а их
объединение совпадает с множествомХ,
т.е. имеем разбиение множества на классы.
Итак, если на множестве Х задано отношение эквивалентности, то оно порождает разбиение этого множества на попарно непересекающиеся подмножества – классы эквивалентности.
частичного порядка (англ. partial order) — рефлексивное антисимметричное транзитивное;
Бинарное
отношение ![]() на
множестве
на
множестве![]() называетсяотношением
частичного порядка (англ. partial
order relation),
если оно обладает следующими свойствами:
называетсяотношением
частичного порядка (англ. partial
order relation),
если оно обладает следующими свойствами:
Рефлексивность (англ. reflexivity):
 .
.Антисимметричность (англ. antisymmetry):
 если
если и
и ,
то
,
то .
.Транзитивность (англ. transitivity):
 если
если и
и ,
то
,
то .
.
«больше или равно» и «меньше или равно» — нестрогого, причем линейного порядка, но не полного.
Отношение «является делителем» на множестве натуральных чисел является отношением частичного порядка.
строгого порядка (англ. strict order) — антирефлексивное антисимметричное транзитивное;
Бинарное
отношение ![]() на
множестве
на
множестве![]() называетсястрогим
отношением частичного порядка (англ. strict
order relation),
если оно обладает следующими свойствами:
называетсястрогим
отношением частичного порядка (англ. strict
order relation),
если оно обладает следующими свойствами:
Антирефлексивность (англ. irreflexivity):
 —
не выполняется.
—
не выполняется.Антисимметричность (англ. antisymmetry):
 если
если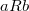 и
и ,
то
,
то .
.Транзитивность: (англ. transitivity)
 если
если и
и ,
то
,
то .
.
На множестве вещественных чисел отношения «больше» и «меньше» являются отношениями строгого порядка
линейного порядка (англ. total order) — полное антисимметричное транзитивное;
Если отношение порядка обладает еще и свойством связанности, то говорят, что оно является отношением линейного порядка. Например, отношение «меньше» на множестве натуральных чисел.
Бинарное
отношение ![]() на
множестве
на
множестве![]() называетсяотношением
линейного порядка (англ. total
order relation),
если оно является отношением частичного
порядка и обладает следующим
свойством:
называетсяотношением
линейного порядка (англ. total
order relation),
если оно является отношением частичного
порядка и обладает следующим
свойством: ![]() либо
либо![]() ,
либо
,
либо![]() .
.
доминирования (англ. dominance) — антирефлексивное антисимметричное.
толерантности
Отношением толерантности (или просто толерантностью) на множестве X называется бинарное отношение, удовлетворяющее свойствам рефлексивности и симметричности, но не обязательно являющееся транзитивным. Таким образом, отношение эквивалентности является частным случаем толерантности.
В отличие от отношения эквивалентности, дающего разбиение множества элементов, на котором оно определено, на непересекающиеся подмножества, отношение толерантности даёт покрытие этого множества. Отношение толерантности используется, например, также при классификациях информации в базах знаний.
На содержательном уровне толерантность означает следующее. Любой объект неразличим сам с собой (свойство рефлексивности), а сходство двух объектов не зависит от того, в каком порядке они сравниваются (свойство симметричности). Однако, если один объект сходен с другим, а этот другой — с третьим, то это вовсе не значит, что все три объекта схожи между собой (таким образом, свойство транзитивности может не выполняться).
Отношение толерантности часто используется для описания отношения сходства между реальными объектами, отношений знакомства или дружбы между людьми. Во всех этих случаях свойство транзитивности не предполагается обязательно быть выполненным. В самом деле, Иванов может быть знаком с Петровым, Петров — с Сидоровым, но при этом Иванов и Сидоров могут быть незнакомы между собой.
Толерантным также будет и отношение на множестве слов, при котором оно задаётся как наличие хотя бы одной общей буквы. В этом случае, например, в отношении находятся пересекающиеся слова кроссворда.
Примеры отношений
Примеры рефлексивных отношений: равенство, одновременность, сходство.
Примеры нерефлексивных отношений: «заботиться о», «развлекать», «нервировать».
Примеры транзитивных отношений: «больше», «меньше», «равно», «подобно», «выше», «севернее».
Примеры симметричных отношений: равенство (=), неравенство, отношение эквивалентности, подобия, одновременности, некоторые отношения родства (например, отношение братства).
Примеры антисимметричных отношений: больше, меньше, больше или равно.
Примеры асимметричных отношений: отношение «больше» (>) и «меньше» (<).
Бинарное
отношение ![]() на
множестве
на
множестве![]() называетсяотношением
эквивалентности (англ. equivalence
binary relation),
если оно обладает следующими свойствами:
называетсяотношением
эквивалентности (англ. equivalence
binary relation),
если оно обладает следующими свойствами:
Рефлексивность:
 .
.Симметричность:
 если
если ,
то
,
то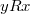 .
.Транзитивность:
 если
если и
и ,
то
,
то .
.
Отношение
эквивалентности обозначают символом ![]() .
Запись вида
.
Запись вида![]() читают
как "
читают
как "![]() эквивалентно
эквивалентно![]() "
"
Примеры:
Отношение равенства(
 )
является тривиальным примером отношения
эквивалентности на любом множестве.
)
является тривиальным примером отношения
эквивалентности на любом множестве.Отношение равенства по модулю
 :
:  на
множестве целых чисел.
на
множестве целых чисел.Отношение параллельности прямых на плоскости.
Отношение подобия фигур на плоскости.
Отношение равносильности на множестве уравнений.
Отношение связности вершин в графе.
Отношение быть одного роста на множестве людей.
Система
непустых
подмножеств ![]() множества
множества![]() называетсяразбиением (англ. partition)
данного множества, если:
называетсяразбиением (англ. partition)
данного множества, если:

 при
при  .
.
Множества ![]() называютсяклассами данного
разбиения.
называютсяклассами данного
разбиения.
Если
на множестве M задано отношение
эквивалентности ![]() ,
то оно порождает разбиение этого
множества наклассы
эквивалентности такое,
что:
,
то оно порождает разбиение этого
множества наклассы
эквивалентности такое,
что:
любые два элемента одного класса находятся в отношении

любые два элемента разных классов не находятся в отношении

Семейство
всех классов эквивалентности множества
образует множество, называемое фактор-множеством,
или факторизацией множества ![]() по
отношению
по
отношению![]() ,
и обозначаемое
,
и обозначаемое![]() .
.
Равенство - классический пример отношения эквивалентности на любом множестве.
