
- •1. Классификация измерений.
- •2. Классификация средств измерений.
- •3. Характеристики средств измерений.
- •4. Способы выражения и нормирования пределов допускаемых погрешностей.
- •5. Погрешности измерений и обработка результатов измерений. Вероятностные оценки ряда наблюдений.
- •6. Общие сведения об электромеханических приборах.
- •7. Магнитоэлектрические измерительные механизмы.
- •8. Магнитоэлектрические амперметры и вольтметры.
- •9. Магнитоэлектрические омметры.
- •10. Выпрямительные приборы.
- •11. Электромагнитные приборы.
- •12. Электродинамические измерительные механизмы.
- •13. Электродинамические амперметры, вольтметры и ваттметры.
- •14. Электронный осциллограф.
- •15. Цифровые приборы. Общие сведения, классификация, погрешности.
- •16. Время-импульсный цифровой вольтметр.
- •17. Цифровой вольтметр сравнения и вычитания.
- •18. Интегрирующий цифровой вольтметр.
- •19. Цифровые частотомеры и фазометры.
- •20. Мосты постоянного и переменного тока. Общие сведения.
- •21. Мост для измерения индуктивности и добротности катушки
- •22. Мост для измерения ёмкости и угла потерь конденсатора.
- •23. Компенсатор постоянного тока.
- •24. Неэлектрические реостатные преобразователи.
- •25. Тензочувствительные преобразователи (тензорезисторы).
- •26. Резистивные термочувствительные преобразователи.
- •27. Индуктивные преобразователи.
- •28. Ёмкостные преобразователи.
- •29. Термоэлектрические преобразователи (термопары).
- •30. Электрический термометр сопротивления.
- •31. Термоэлектрические термометры.
4. Способы выражения и нормирования пределов допускаемых погрешностей.
Погрешности могут выражаться в виде:
- абсолютном; - относительном; - приведённом;
- числа делений шкалы.
Абсолютная погрешность - это разница между истинным и полученным значением измеряемой величины:

Предел допускаемой абс. погрешности выражается:
1)
одним значением:

2)
двучленной формулой

Нормирование (установление предела абс. погрешности) по пункту а) производится, если мультипликативная составляющая погрешности отсутствует или отдельно не учитывается. По пункту б) - если учитывается отдельно мультипликативная составляющая.
Недостаток абс. погрешности - невозможность сравнения СИ разного назначения.
Относительная погрешность - это отношение абсолютной погрешности к значению измеряемой величины:

Предел относительной погрешности выражается:
а)

б)
 ,
где
,
где и
и - константы,
- константы, конечное значение диапазона измерений,
конечное значение диапазона измерений, - результат измерений.
- результат измерений. и
и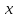 берутся
без учёта знака.
берутся
без учёта знака.
Нормирование - так же как с абсолютной.
Недостаток:
при
 .
.
Приведённая погрешность - это отношение абсолютной погрешности к нормирующему значению. Применяется только если мультипликативная погрешность отсутствует или отдельно не учитывается.

В качестве нормирующего значения берут:
а) верхний предел диапазона измерений, если нижний предел равен нулю либо ноль находится вне диапазона;
б) сумму модулей верхнего и нижнего пределов, если нуль находится внутри диапазона.
Класс точности - обобщённая метрологическая характеристика СИ, определяющая допускаемые пределы основных и дополнительных погрешностей, а также другие св-ва этого средства, влияющие на точность результатов измерений. Для обозначения классов точности применяются следующие числа:

Для СИ, у которых погрешность нормируют в виде предела приведённой погрешности, класс точности численно равен этому пределу. Абс. и отн. погрешности в таком случае оцениваются по формулам:
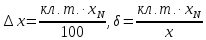
Правила округления погрешности:
а) не более 2-х значащих цифр;
б) результат округляют "по погрешности", т. е. последний разряд результата должен соответствовать последней цифре погрешности.
Если
предел допускаемой погрешности
определяется по двучленной формуле,
то в обозначении класса точности
вводятся числа
 и
и ,
, :
:

Напр.: 0.05/0.02
5. Погрешности измерений и обработка результатов измерений. Вероятностные оценки ряда наблюдений.
Погрешности измерений делятся на систематические (методические, инструментальные, погрешность установки приборов) и случайные (обнаруживаются при многократных измерениях, проводимых с одинаковой тщательностью и при одних и тех же условиях).
Результат измерения всегда содержит как систематическую, так и случайную погрешность:
 ,
где первый член - это систематич.
погрешность (мат. ожидание), а второй -
случайная погрешность. Поэтому
погрешность измеряемой величины в
общем случае рассматривается как
случайная величина.
,
где первый член - это систематич.
погрешность (мат. ожидание), а второй -
случайная погрешность. Поэтому
погрешность измеряемой величины в
общем случае рассматривается как
случайная величина.
Полным
описанием случайной величины, а,
следовательно, и случайной погрешности,
является закон распределения. Наиболее
часто встречающийся - нормальный закон
распределения (Гаусса)
 ,
основанный на 2-х аксиомах:
,
основанный на 2-х аксиомах:
1. При большом числе измерений погрешности, одинаковые по величине и разные по знаку, встречаются одинаково часто.
2. Малые погрешности встречаются чаще, чем большие.
![]()
![]()
 плотность
распределения.
плотность
распределения.

Основными характеристиками закона распределения являются мат. ожидание и дисперсия.
Мат. ожидание ряда измерений есть величина, относительно которой рассеиваются результаты отдельных измерений. Если систематич. погрешность отсутствует и разброс обусловлен только случайной погрешностью, то мат. ожиданием будет истинное значение случайной величины.

Дисперсия ряда наблюдений характеризует разброс результатов отдельных измерений вокруг мат. ожидания.

Т.
к. дисперсия измеряется в квадратных
единицах, то в качестве х-ки измерений
применяют СКО

Обработка результатов измерений
Обычно МО и СКО неизвестны и их оценивают по результатам полученного ряда наблюдений.
Оценкой
МО является среднее
арифметическое
результатов отдельных наблюдений:
 .
.
Разница между каждым отдельным значение и ср. арифметическим называется случайным отклонением или остаточной погрешностью:

При неограниченно большом числе измерений среднее арифметическое стремится к мат. ожиданию:

Оценка
дисперсии:
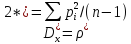
При
неограниченно большом числе измерений
(реально при
 ):
):
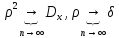
Т.
о.
 можно принять за действительное
значение, а МО - за истинное. Оценить
близость действительного значения к
истинному можно с помощьюдоверительного
интервала.
можно принять за действительное
значение, а МО - за истинное. Оценить
близость действительного значения к
истинному можно с помощьюдоверительного
интервала.![]()
Это
интервал погрешностей, в котором
погрешность находится с заданной
вероятностью, которая называется
доверительной. В общем случае доверительный
интервал может быть установлен, если
известен закон распределения погрешности
с основными его характеристикам, и
выбирается в зависимости от конкретных
условий измерений. При нормальном
законе распределения пользуются обычно
доверительным интервалом
 .
Это означает, что из 370 погрешностей
только 1 по абсолютной величине м. б.
больше
.
Это означает, что из 370 погрешностей
только 1 по абсолютной величине м. б.
больше

Среднее арифметическое является случайной величиной.
Дисперсия среднего арифметического в n раз меньше дисперсии ряда наблюдений, из которого оно получено:
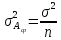 .
Если
дисперсия
.
Если
дисперсия
 неизвестна (мало число опытов), то её
оценивают по остаточным погрешностям:
неизвестна (мало число опытов), то её
оценивают по остаточным погрешностям: .
.
Для
нахождения доверительного интервала
необходимо найти закон распределения
величины
 =
= при известной дисперсии (
при известной дисперсии ( )
или
)
или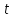 =
= при неизвестной дисперсии.
при неизвестной дисперсии.
Для
нормального закона Z есть случайная
величина с
 и
и ,
а
,
а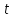 - случайная величина, распределённая
по закона Стьюдента. Чем больше число
измерений, тем ближе
- случайная величина, распределённая
по закона Стьюдента. Чем больше число
измерений, тем ближе совпадает с
совпадает с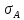 и закон Стьюдента приближается к
нормальному.
и закон Стьюдента приближается к
нормальному.
Зная Z или t, результат измерения с определённой доверительной вероятностью может быть записан как
 при
известной дисперсии;
при
известной дисперсии;
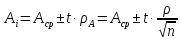 при
неизвестной дисперсии.
при
неизвестной дисперсии.
Увеличение числа опытов уменьшает доверит. интервал.
