Добавил:

AJIEIIIKA ajieiiika26@gmail.com Делаю контрольные работы, курсовые, дипломные работы. Писать на e-mail. Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ивановский Государственный Энергетический Университет им. В.И. Ленина

Предмет:

Тепловые и атомные электростанции

Файл:

Цветков задачник по тепломасообмену

.pdf

Скачиваний:

3026

Добавлен:

18.01.2018

Размер:

2.6 Mб

Скачать

☆

1 / 201 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

УДК 621.396.669.8 ББК 32.84

Ц 274

Ре ц е н з е н т ы : академик РАН А.И. Леонтьев, доктор технических наук, профессор Э.Д. Сергиевский

Цветков Ф.Ф.

Ц 274 Задачник по тепломассообмену : учебное пособие / Ф.Ф. Цветков, Р.В. Керимов, В.И. Величко. — 2-е изд., исправ. и доп. — М.: Издательский дом МЭИ, 2008. — 196 с., ил.

ISBN 978-5-383-00259-9

В учебном пособии представлены задачи по всем разделам курса «Тепломассообмен» — составной части дисциплины «Теоретические основы теплотехники». В начале каждой главы приводятся основные формулы и примеры решения задач. Все задачи снабжены ответами; приложения содержат справочный материал, необходимый для решения задач.

Предназначено для студентов вузов, специализирующихся в области теплоэнергетики, промышленной теплоэнергетики, технической физики, энергомашиностроения.

УДК 621.396.669.8 ББК 32.84

	© Цветков Ф.Ф., Керимов Р.В., Величко В.И., 2008
ISBN 978-5-383-00259-9	© ЗАО «Издательский дом МЭИ», 2008

ПРЕДИСЛОВИЕ

Предлагаемое пособие представляет собой сборник задач по тепломассообмену — базовой дисциплине для специальностей теплоэнергетического профиля. При написании данного пособия авторы учитывали опыт использования первого издания задачника (1997 г.) на практических аудиторных занятиях и в домашней работе студентов. В частности, наряду с увеличением количества задач авторы сочли целесообразным привести примеры решения задач по всем разделам курса и дать перечень математических выражений основных закономерностей тепломассообмена, расчетных формул к каждой главе задачника. При составлении перечня формул авторы использовали список литературы, приведенный в конце пособия и, в первую очередь, книгу [11].

Главы первая и вторая написаны Р.В. Керимовым и Ф.Ф. Цветковым, глава пятая — Р.В. Керимовым, главы третья и четвертая — В.И. Величко, главы с шестой по двенадцатую — Ф.Ф. Цветковым.

Авторы благодарны преподавателям кафеды ТОТ им. М.П. Вукаловича Московского энергетического института (технического университета) за ряд замечаний, направленных на улучшение содержания данного учебного пособия.

Авторы

СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ

ОБОЗНАЧЕНИЯ ВЕЛИЧИН

а — коэффициент температуропроводности, м2/с;

А — поглощательная способность;

с— теплоемкость, Дж/(кгæК); массовая концентрация;

d — диаметр, м;

D — коэффициент диффузии, м2/с;

Е— плотность потока излучения, Вт/м2;

F — площадь поверхности, м2;

g — ускорение силы тяжести, м/с2;

G — расход, кг/с;

h — высота, м; энтальпия, Дж/кг;

I — интенсивность излучения, Вт/(м2æср);

j — плотность диффузионного потока массы, кг/(м2æс);

J— плотность полного (диффузионного и конвективного) потока

массы, кг/(м2æс);

k — коэффициент теплопередачи, Вт/(м2æК);

l — длина, м;

р — давление, Па;

p — перепад давлений, Па;

q — плотность теплового потока, Вт/м2;

ql — линейная плотность теплового потока, Вт/м;

Q — тепловой поток, Вт; qv — мощность внутренних

источников теплоты, Вт/м3;

r— радиус, м; теплота испарения, Дж/кг;

R— термическое сопротивление, м2æК/Вт; отражательная способность;

t — температура, °С;

Т — температура, К;

w — скорость, м/с;

х— координата, м; массовое расходное паросодержание;

α— коэффициент теплоотдачи, Вт/(м2æК);

β— коэффициент массоотдачи, кг/(м2æс); коэффициент объемного расширения, К–1;

δ— толщина стенки, м; толщина пограничного слоя, м;

ε — степень черноты;

Θ — безразмерная температура;

λ— коэффициент теплопроводности, Вт/(мæК); длина волны излучения, м;

μ — динамическая вязкость, Паæс;

ν — кинематическая вязкость, м2/с;

ξ— коэффициент гидравлического сопротивления;

ρ — плотность, кг/м3;

σ0 — постоянная Стефана—Больц- мана, Вт/(м2æК4);

σ— коэффициент поверхностного натяжения, Н/м;

τ — время, с.

ЧИСЛА ПОДОБИЯ

αl0			—	число Био;
Bi = -------			—	число Био;
λ
ατ			—	число Фурье;
Fo = ------			—	число Фурье;
l02
gβ t	0l	03	—	число Грасгофа;
Gr = ------------------			—	число Грасгофа;
ν2
Ra = GræPr			—	число Рэлея;
D
Le = --- — число Льюиса;
a
αl0

Nu = ------- —число Нуссельта;

СОКРАЩЕНИЯ, ИНДЕКСЫ

с — стенка; ж — жидкость; из — изоляция;

ш — шероховатость;

п— пар;

вн — внутренний; вш — внешний; эл — электрический;

г— газ;

пс — пограничный слой;

×— относится к параметру вдали от поверхности или от входа в канал;

экв — эквивалентный; тур — турбулентный; лам — ламинарный; смеш — смешанный;

н.т — начальный термический; н.г — начальный гидравлический;

0— относится к масштабной величине системы; абсолютно черное тело;

— — знак усреднения; вх — вход;

	βl	0
	-------			—	диффузионное
NuD = ρD				—	диффузионное
					число Нуссельта;
wl0				—	число Пекле;
Pe = --------				—	число Пекле;
	a
	ν		μcp	—	число Прандтля;
Pr = ---- =			--------	—	число Прандтля;
	a		λ
	ν
PrD =	------			—	диффузионное
PrD =	D			—	диффузионное
					число Прандтля;
Re =	wl0		ρwl0		— число Рейнольдса.
Re =	--------	= -----------			— число Рейнольдса.
	ν		μ

р — ребро; кр — критический; вых — выход;

пр — предельный; продувка; приведенный;

гр — граничный; граница; п.к — поверхностное кипение; см — смесь; пл — пленка;

ф— фаза;

с.п	— стефанов поток;
пад	— падающий;
соб	— собственный;
рез	— результирующий;
эф	— эффективный;
тр	— трение; труба;
уск	— ускорение;
м	— местный;
пот	— потери;
верт — вертикальный;
гор	— горизонтальный;
шах	— шахматный;
кор	— коридорный;
п.м	— погонный метр.

Ч а с т ь п е р в а я

ТЕПЛОПРОВОДНОСТЬ

Г л а в а п е р в а я

СТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ

ОСНОВНЫЕ ФОРМУЛЫ

А. Плоская стенка

Температурное поле в плоской стенке:

t =

tс1 –

tс1

– t

с2

x при λ = const;

-------------------

2qx

при λ = λ

t =

+ t

–

(1 + bt).

---

– --------

---

с1

Плотность теплового потока через плоскую стенку:

q =

tс1 – t

с2

q =

tс1 – tс, n + 1

------------------- ;

---------------------------- при λ = const;

-δ-

∑ λ i

i = 1

ср

tс2 ) ,

q = ------ (tс1 –

где при λ = λ0(1 + bt)

	1		tc2						+ btс1 + tс2
λcp =	1			∫ λ(t) dt		= λ0		1	+ btс1 + tс2	;
	tс2 – tс1		t						2
	tс2 – tс1		t	c1
				c1
	q =			tж1 – tж2				= k tж ,
	q =	1		n	δ	+	1	= k tж ,
		-----	+ ∑		--	+	-----
		α1		i = 1	λ i		α2
				i = 1

(1.1)

(1.2)

(1.3)

(1.4)

(1.5)

Г л а в а п е р в а я . СТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ

где k =		1		— коэффициент теплопередачи.
где k =		n		— коэффициент теплопередачи.
		n
Rα	1	+ ∑ Rλ, i	+ Rα	2
	1			2

i = 1

Б. Цилиндрическая стенка

3. Температурное поле в цилиндрической стенке:

	t = tc1 –		tc1 – tc2	ln	r		при λ = const;
	t = tc1 –		-------------------r2	ln	r----1		при λ = const;
			-------------------r2		r----1
			ln ----
			r1
	1		ql ln	----r
	1		2	r1 1
t =	--- + t		– ----------------		–	---	при λ = λ (1 + bt).
	b	c1	πbλ	0		b	0
				0

(1.6)

(1.7)

4. Линейная плотность теплового потока через цилиндрическую стенку:

π(tc1

– tc2 )

ql =

π(tc1

– tc, n + 1 )

при λ = const;

= ---------------------------

;

-------1 ln di + 1

--1----

2λ

∑

2λ

i = 1

π(tc1

– tc2 )

ql = ---------------------------

;

2----------λcp

ln d----1

tc1 + tc2

при λ = λ0(1 + bt),

λср = λ0

1 + -------------------

;

π(tж1

– tж2 )

----------------------------------------------------------------------------------------

1 ln di + 1

-----------

+ ∑

+ ------------------

i = 1

2λi

n + 1

5. Критический диаметр тепловой изоляции:

dкр. из =

2λиз

----------

α2

(1.8)

(1.9)

(1.10)

(1.11)

Ча с т ь п е р в а я . ТЕПЛОПРОВОДНОСТЬ

В.Теплопроводность ребер

6. Температурное поле в ребре постоянного по длине поперечного сечения:

		ϑ		= ϑ		æе–mx — ребро бесконечной длины;					(1.12)
			x		0
		ϑx = ϑ0			ch [m(l – x)]
					---------------------------------		— ребро конечной длины,				(1.13)
						ch (ml)	— ребро конечной длины,				(1.13)
						ch (ml)
где т	=	αu	;	u и		f — периметр и площадь поперечного сечения
где т	=	------	;	u и		f — периметр и площадь поперечного сечения
		λf
ребра, ϑ0 = t0 – tж.
7.	Тепловой поток с поверхности ребра (f = const):
	Qp = ϑ0mλf = ϑ0 αuλf						для ребра бесконечной длины; (1.14)
Qp = ϑ0			αuλf			th (ml) = ϑ0αul		th (ml)
								-----------------		для ребра конечной
									ml	для ребра конечной
									ml
										длины.	(1.15)
8.	Коэффициент эффективности ребра
						Eр =	th (ml)		.		(1.16)
						Eр =	-----------------		.		(1.16)

Г. Внутренние источники тепла

9. Температурное поле при наличии внутренних источников тепла:

		q δ	q		2		2
tx	= tж	v 0	v	(δ	2	– x	2	)	(1.17)
tx	= tж	+ ---------	+ -----	(δ	0	– x		)	(1.17)
		α	2λ
— в плоской стенке толщиной 2δ0 (плоский твэл);
tr	= tж	qv r0	qv	(r	2	– r	2	)	(1.18)
tr	= tж	+ ----------	+ -----	(r	0	– r		)	(1.18)
		2α	4λ

—в цилиндрическом стержне радиусом r0 (цилиндрический твэл).

10.Плотность теплового потока на поверхности твэла:

qс = qvδ0 (плоского); qс =	qv r	0	(цилиндрического).	(1.19)
	----------
	2

Г л а в а п е р в а я . СТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ

ЗАДАЧИ

1.1. Плоская стенка выполнена из материала с коэффициентом теплопроводности λ = 20 Вт/(мæК). Толщина стенки δ = 10 мм. На одной стороне стенки температура tс1 = 100 °С, на другой 90 °С.

Найти плотность теплового потока через стенку и температуру в середине стенки.

Решение. По формуле (1.3) определяем

20(100 – 90) 2 q = ------------------------------- = 20 000 Вт/м .

10æ10– 3

Так как при λ = const температура в стенке изменяется по линейному закону, то в середине стенки

tсер	1	1
tсер	= --- (tc1	+ tc2) = --- (100 + 90) = 95	°C.
	2	2

Ответ. q = 20 кВт/м2; tсер = 95 °С.

1.2. В теплообменнике горячий и холодный теплоносители разделены плоской латунной стенкой [δ = 2 мм, λ = 100 Вт/(мæК)], перепад температур в которой tс1 – tс2 = 5 °C. Вычислить плотность теплового потока через стенку. Определить толщину стальной [λ = = 45 Вт/(м æК]) и медной [λ = 370 Вт / (мæК)] стенок, чтобы при том же перепаде температур плотность теплового потока осталась неизменной.

1.3.Чему равен тепловой поток через стену из красного кирпича высотой 4 м, шириной 5 м и толщиной 500 мм? На одной поверхности стены температура 19 °С, на другой 2 °С.

1.4.Вычислить плотность теплового потока через оконное стекло толщиной δ = 3 мм, если температуры его поверхностей tс1 = 1 °С

иtс2 = –1 °С. Известно, что плотность, теплоемкость и коэффициент

температуропроводности стекла составляют соответственно ρ = = 2500 кг/м3, cр = 0,67 кДж/(кг æК) и а = 4,42 æ10–7 м2/с.

1.5. Плотность теплового потока через плоскую стенку толщиной

200 мм составляет 200 Вт/м2, а разность температур ее поверхностей 50 °С. Определить коэффициент температуропроводности стенки,

если ρ = 1700 кг/м3, cр = 0,88 кДж/(кг æК).

Ч а с т ь п е р в а я . ТЕПЛОПРОВОДНОСТЬ

tс1			tс1
1			1
2
			d
tс2			tс2
5 мм			tс2
5 мм			5 мм
			5 мм
3
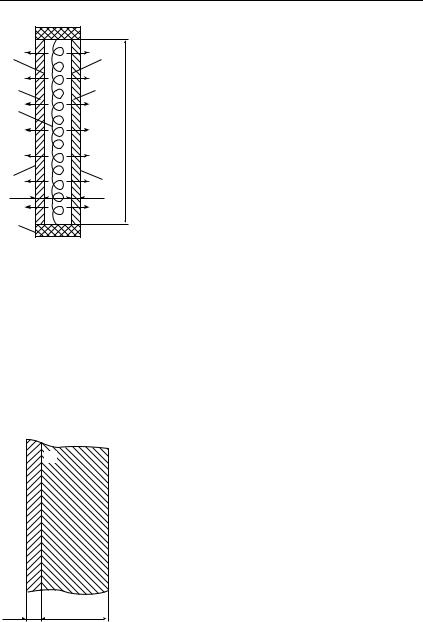
Рис. 1.1. К задаче 1.6:
1 — образцы; 2 — нагре-
ватель;	3	—	кольцевая
изоляция

1.6. К двум торцам нагревателя цилиндрической формы d = 300 мм плотно прижаты два идентичных образца материала того же диаметра толщиной δ = 5 мм. Определить коэффициент теплопроводности образцов, если при мощности нагревателя Q = 56,5 Вт перепады температур по толщине образцов составили 12,5 °С. Радиальный перенос тепла в системе пренебрежимо мал (рис. 1.1).

1.7.Дана трехслойная плоская стенка: δ1 =

=20 мм; λ1 = 20 Вт/(м æК); tс1 = 10 °С; λ2 =

=5 + 0,05t Вт/(мæК); tс4 = 60 °С; δ3 = 60 мм; λ3 = 10 Вт/(мæК); tж2 = 150 °С; α2 =

=18 Вт/(м2 æК). Найти δ2.

1.8. Плоскую поверхность с tс = 250 °С решено изолировать листо-

вым асбестом, у которого λ = 0,157 + (0,14æ10–3)t Вт/(мæК). Какой толщины должен быть слой изоляции, если допустимая температура наружной ее поверхности 50 °С, а тепловые потери не должны пре-

вышать 500 Вт/м2 ?

tс1. .tс2
Топка	Окружающая среда
	.tс3
120	500

Рис. 1.2. К задаче 1.9

1.9. Внутренний слой стен топочной камеры парового котла выполнен из шамотного кирпича (δш = 120 мм), наруж-

ный слой — из пеношамота (δп = 500 мм), плотно прилегающих друг к другу. Температуры на соответствующих поверхностях пеношамота составляют tс2 = 800 °С и tс3 = 60 °С. Вычислить температуру на внутренней поверхности слоя из шамотного кирпича с учетом зависимости его коэффициента теплопроводности от температуры (рис. 1.2).

1.10. Стены сушильной камеры толщиной 0,256 м, выполненные из слоя крас-

1 / 201 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

Соседние файлы в папке Тепломассообмен

#
18.01.20181.21 Mб351Раздел РТО Тмо.pdf
#
18.01.2018899.84 Кб180Расчет конвективной теплоотдачи.pdf
#
18.01.20182.65 Mб276Справочные материалы по тмо.pdf
#
18.01.201812.21 Кб130ТМО экзвопр.docx
#
18.01.20182.06 Mб1299ТОТ в примерах и задачах.pdf
#
18.01.20182.6 Mб3026Цветков задачник по тепломасообмену.pdf