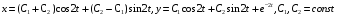Задача 6

Вычислите несобственный интеграл первого рода (если он сходиться) .

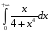Решение.

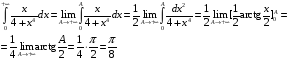
Задача 9

Найдите общее решение (или общий интеграл) дифференциального уравнения первого порядка .

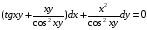Решение.

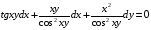
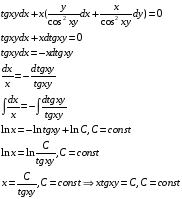
Ответ: .

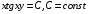Задача 10

Найдите общее решение (или общий интеграл) дифференциального уравнения первого порядка .

Решение.

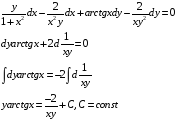
Ответ:

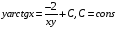
Задача 11

Найдите общее решение (или общий интеграл) дифференциального уравнения первого порядка

Решение.

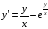
_{Решим для начала}

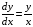
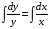
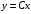
_{Предполагаем, что} .

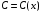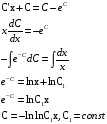
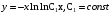
_Ответ:

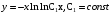
Задача 12

Найдите общее решение (или общий интеграл) дифференциального уравнения первого порядка

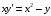
Решение.

Произведем подстановку ,

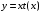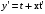
Подставляет в первоначальное уравнение:

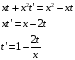
Решим для начала уравнение

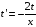
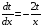
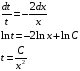
Представим, что 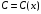, тогда получим .

Подставим в уравнение .

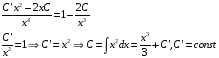
Получаем

Произведем обратную замену .

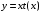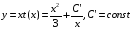
Ответ:

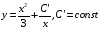
Задача 13

_{Решите задачу Коши}

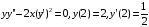
_{Решение. Проведем замену}

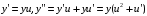
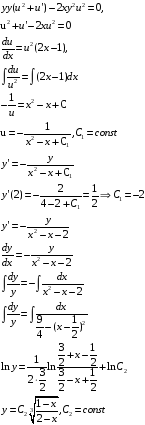
_{Найдем решение для начальных условий}

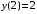
Получили деление на 0. Значит, у заданного начального условия нет решений.

Задача 14

Найдите уравнение кривой, проходящей через точку , если в любой ее точке М касательный вектор 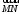(с концом N на оси ординат) имеет длину, равную 20, и образует острый угол с положительным направлением оси ординат.

Решение.

Точка N имеет координаты 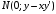. Длина вектора

_{Составим уравнение}

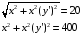
Произведем замену .

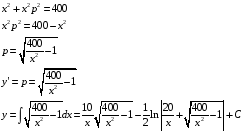
Подставим точку

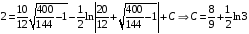
Ответ:

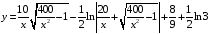
Задача 15

Найдите частное решение линейного однородного дифференциального уравнения, удовлетворяющее заданным начальным условиям.

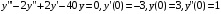
Решение.

Решим однородное уравнение:

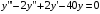
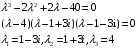
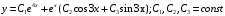
Найдем частное решение

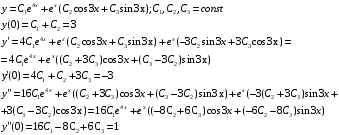
_{Решим систему уравнение}

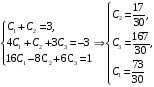
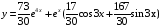
_Ответ:

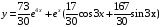
Задача 16

Решите линейную неоднородную систему дифференциальных уравнений

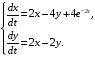
Решение.

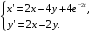
Из второго уравнения выразим х:

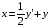
Найдем первую производную и подставим в первое уравнение системы:

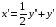
Решим однородное уравнение:

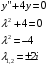
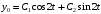
Найдем частное решение в виде

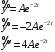
Подставляем в уравнение

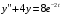
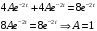
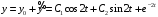
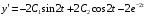
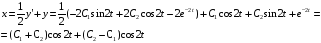
Ответ: