
ИПР3-2(15 вариант)
.docxИндивидуальная практическая работа ИПР3-2
Вариант 15
Задача 1. Постройте на комплексной
плоскости область
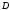 ,
заданную системой неравенств. Проверьте,
принадлежит ли заданная точка
,
заданную системой неравенств. Проверьте,
принадлежит ли заданная точка
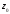 области
области
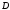 .
.

Решение.
Неравенство
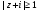 соответствует внешней части круга
радиусом
соответствует внешней части круга
радиусом
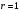 с центром в точке
с центром в точке
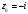 ,
включая ограничивающую его окружность.
,
включая ограничивающую его окружность.
Неравенство
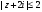 соответствует внутренней части круга
радиусом
соответствует внутренней части круга
радиусом
 с центром в точке
с центром в точке
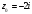 ,
включая ограничивающую его окружность.
,
включая ограничивающую его окружность.
Неравенство
 соответствует сектору окружности. На
рисунке представлена область
соответствует сектору окружности. На
рисунке представлена область
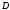 .
.

Точка
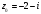 не принадлежит области
не принадлежит области
 .
Проверим это аналитически:
.
Проверим это аналитически:
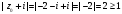 - неравенство выполнено.
- неравенство выполнено.
 -
неравенство не выполнено.
-
неравенство не выполнено.
 - неравенство не выполнено.
- неравенство не выполнено.
Значит, точка
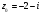 не принадлежит области
не принадлежит области
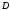 .
.
Задача 2. Определите область (круг)
сходимости данного комплексного ряда.
Исследуйте его сходимость (сходится
абсолютно, сходится условно, расходится)
в точках
 ,
,
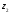 ,
,
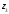 .
.
 ;
;
 ,
,
 ,
,
 .
.
Решение.
Применим признак Даламбера:
 ,
,
 .
.
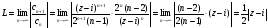
Отсюда,
следовательно, ряд сходится при условии
 или внутри круга
или внутри круга
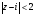 радиусом
радиусом
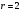 с центром в точке
с центром в точке
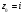 .
.
На рисунке изображены точки, которые необходимо исследовать и область сходимости.
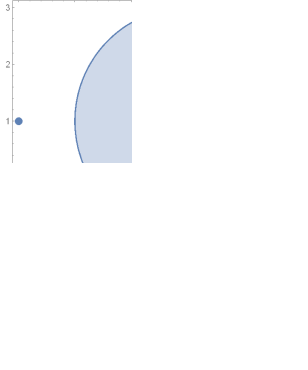
Точка
 расположена на границе круга сходимости,
т.к.
расположена на границе круга сходимости,
т.к.
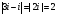 .
Для исследования сходимости заданного
ряда в этой точке подставим её в ряд:
.
Для исследования сходимости заданного
ряда в этой точке подставим её в ряд:
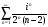 .
.
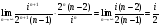 .
.
Таким
образом, исходный ряд сходится абсолютно
в точке
 при
при
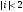 .
.
Точка
 расположена внутри круга сходимости,
т.к.
расположена внутри круга сходимости,
т.к.
 ,
поэтому ряд в ней сходится абсолютно.
,
поэтому ряд в ней сходится абсолютно.
Точка
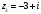 расположена
вне круга сходимости, т.к.
расположена
вне круга сходимости, т.к.
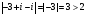 ,
поэтому ряд в ней расходится.
,
поэтому ряд в ней расходится.
Задача
3. Проверьте, является и функция
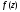 аналитической в области
аналитической в области
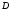 .
Вычислите интеграл от этой функции по
указанной кривой
.
Вычислите интеграл от этой функции по
указанной кривой
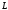 .
.
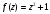 ;
;
 ;
;
 – ломаная
– ломаная
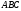 :
:
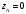 ,
,
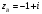 ,
,
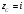 .
.
Решение.
Для
проверки того, является ли функция
аналитической, воспользуемся условиями
Коши-Римана. Для этого с помощью формулы
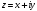 представим заданную функцию в виде
представим заданную функцию в виде
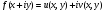 .
С учетом
.
С учетом
 имеем
имеем
 откуда получаем
откуда получаем
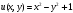 ,
,
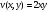 .
.
Найдем частные производные
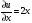 ,
,
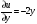 ,
,
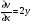 ,
,
 .
.
Теперь проверим выполнение условия Коши-Римана:
 ,
,
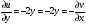 .
.
Так как условия Коши-Римана выполняются
для любых
 и
и
 ,
то функция
,
то функция
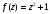 является аналитической на всей комплексной
плоскости, включая и область
является аналитической на всей комплексной
плоскости, включая и область
 .
.
Теперь вычислим интеграл от заданной функции.
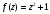
 – ломаная
– ломаная
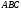 :
:
 ,
,
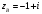 ,
,
 .
.
Заданная
кривая
 представляет собой ломаную
представляет собой ломаную
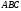 :
:
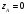 ,
,
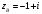 ,
,
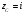 .
.
В данном случае воспользуемся формулой
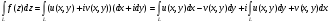 .
.
На
отрезке
 :
:
 .
.
На
отрезке
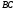 :
:
 .
.
На
отрезке
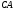 :
:
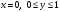 .
.
Вычислим интеграл

Задача
4. Функция
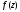 разложена в ряд Лорана в окрестности
своей изолированной особой точки
разложена в ряд Лорана в окрестности
своей изолированной особой точки
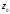 ,
где
,
где
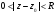 .
.
А)
Определите тип особой точки
 и найдите в ней вычет функции
и найдите в ней вычет функции
 .
.
Б)
Вычислите с помощью вычетов интеграл
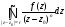 ,
если
,
если
 .
.
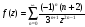 ,
,
 ;
;
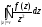 .
.
Решение.

Т.к. функция
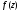 в окрестности изолированной точки
в окрестности изолированной точки
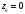 содержит бесконечное число слагаемых
в главной части, то точка
содержит бесконечное число слагаемых
в главной части, то точка
 является существенно особой точкой.
является существенно особой точкой.
Вычетом функции
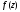 в точке
в точке
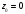 называется коэффициент
называется коэффициент
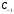 разложения этой функции в ряд Лорана
по степеням
разложения этой функции в ряд Лорана
по степеням
 ,
в данном случае
,
в данном случае
 ,
значит,
,
значит,
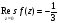 .
.
Рассмотрим интеграл
 .
.

Внутри контура интегрирования
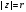 расположена только одна особая точка
подынтегральной функции, которая
согласно ряду Лорана является существенно
особой точкой. Вычет в этой точке равен
расположена только одна особая точка
подынтегральной функции, которая
согласно ряду Лорана является существенно
особой точкой. Вычет в этой точке равен
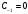 ,
значит,
,
значит,
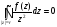 .
.
Задача 5. Найдите все лорановские
разложения функции
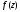 по степеням
по степеням
 .
.
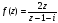 ,
,
 .
.
Решение.
Функция
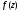 не является аналитической, т.к. имеем
изолированную особую точку
не является аналитической, т.к. имеем
изолированную особую точку
 .
Исключим ее из рассмотрения, разбив
комплексную плоскость на две области
.
Исключим ее из рассмотрения, разбив
комплексную плоскость на две области
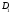 и
и
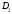 окружностью с центром в точке
окружностью с центром в точке
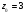 радиусом, равным расстоянию от
радиусом, равным расстоянию от
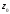 до особой точки:
до особой точки:
 .
.
Найдем
 .
.
Таким образом, имеем
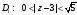 ,
,
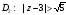 .
.
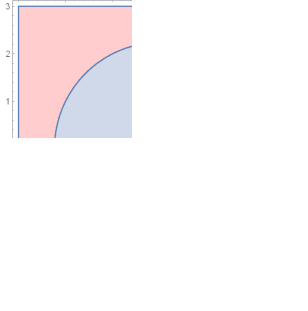
Для удобства разложения в ряд Лорана
преобразуем заданную функцию, выделив
явно выражение
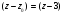 :
:
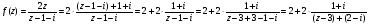
В области
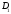 имеем:
имеем:
 .
.
Воспользуемся формулой суммы бесконечно
убывающей геометрической прогрессии,
в области
 выполнено неравенство
выполнено неравенство
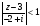 ,
значит,
,
значит,
 .
.
В области
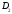 имеем:
имеем:
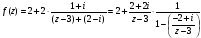 .
.
Воспользуемся формулой суммы бесконечно
убывающей геометрической прогрессии,
в области
 выполнено неравенство
выполнено неравенство
 ,
значит,
,
значит,
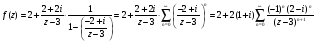 .
.
Таким образом, в разных областях аналитичности функция имеет различные разложения в ряд Лорана.
Задача 6. Дана функция
 .
Найдите её изолированную особую точку
.
Найдите её изолированную особую точку
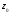 и разложите функцию в ряд Лорана в
окрестности точки
и разложите функцию в ряд Лорана в
окрестности точки
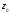 .
С помощью вычетов найдите интегралы
.
С помощью вычетов найдите интегралы
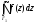 ,
,
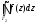 ,
,
 ,
где
,
где
 ,
,
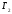 ,
,
 – заданные контуры.
– заданные контуры.
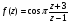 ;
;
 ,
,
 ,
,
 .
.
Решение.
Единственной изолированной особой
точкой функции, очевидно, является
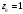 .
Во всех остальных точках комплексной
плоскости функции является аналитической.
.
Во всех остальных точках комплексной
плоскости функции является аналитической.
Для разложения функции в ряд Лорана
преобразуем её следующим образом,
выделив явно
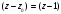 :
:
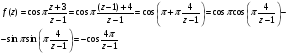
Воспользуемся стандартным разложением косинуса в ряд Тейлора:

Видно, что
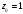 является существенно особой точкой
функции, так как ряд Лорана содержит в
главной части бесконечное число
слагаемых.
является существенно особой точкой
функции, так как ряд Лорана содержит в
главной части бесконечное число
слагаемых.
Для вычисления интеграла изобразим
контуры
 и особую точку функции
и особую точку функции
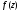 на рисунке.
на рисунке.

Найдем
вычеты функции
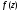 .
В разложении функции в ряд Лорана по
степеням
.
В разложении функции в ряд Лорана по
степеням
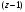 ,
коэффициенту
,
коэффициенту
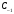 соответствует слагаемое 0.
соответствует слагаемое 0.
Следовательно,
 .
.
Вычислим заданные интегралы:
 ,
т.к. внутри контура расположена только
одна особая точка
,
т.к. внутри контура расположена только
одна особая точка
 функции.
функции.
 ,
т.к. внутри контура расположена только
одна особая точка
,
т.к. внутри контура расположена только
одна особая точка
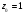 функции.
функции.
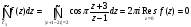 ,
т.к. точка
,
т.к. точка
 расположена вне контура интегрирования.
расположена вне контура интегрирования.
Задача 7. Вычислите интеграл с помощью интегральной формулы Коши. Направление обхода контура – положительное.
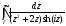 ,
,
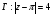 .
.
Решение.
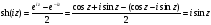 .
.
Подынтегральная функция
 имеет следующие особые точки:
имеет следующие особые точки:
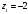 ,
,
 ,
,
 .
.
Изобразим контур интегрирования и особые точки на рисунке.
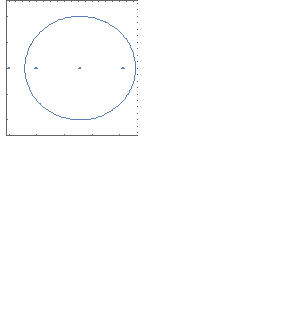
Внутри
контура интегрирования
 расположены точки
расположены точки
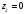 ,
,
 ,
,
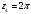 .
Окружим их контурами
.
Окружим их контурами
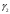 ,
,
 ,
,
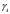 в виде положительно ориентированной
окружности, целиком лежащей внутри
круга
в виде положительно ориентированной
окружности, целиком лежащей внутри
круга
 ,
в результате получим двухсвязную
область. По интегральной теореме Коши
для многосвязной области запишем
,
в результате получим двухсвязную
область. По интегральной теореме Коши
для многосвязной области запишем
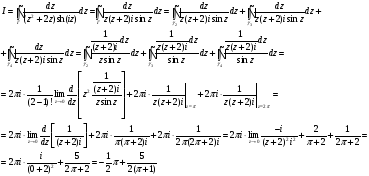
Задача 8. Найдите изображение заданного оригинала.
 .
.
Решение.
Представим заданную функцию-оригинал
в виде
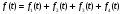 ,
где
,
где
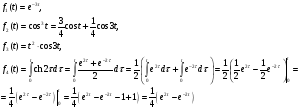
Используя таблицу получим
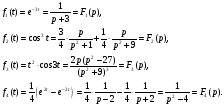
Окончательно по свойству линейности преобразования Лапласа получаем
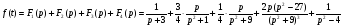
Задача 9. Найдите оригинал по заданному изображению.
 .
.
Решение.
Упростим заданный оригинал, представив его в виде суммы простейших дробей

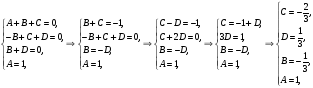

Воспользовавшись свойствами преобразования Лапласа и таблицей оригиналов и изображений, получим
 .
.
Задача 10. Решите дифференциальное уравнение операционным методом.
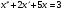 ;
;
 ,
,
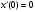 .
.
Решение.
Пусть
правая часть уравнения является
оригиналом, тогда и искомая функция
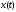 будет оригиналом. Преобразуем обе части
уравнения по Лапласу, воспользовавшись
формулой изображения производной
оригинала:
будет оригиналом. Преобразуем обе части
уравнения по Лапласу, воспользовавшись
формулой изображения производной
оригинала:
 ,
где
,
где
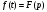 .
.
Имеем
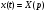 ,
,
 ,
,
 ,
,
 .
.
Операторное уравнение имеет вид
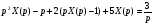 ,
,
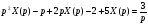 .
.
Выразим
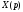 :
:

Упростим данное выражение, представив его в виде суммы простейших дробей:
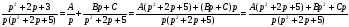

Таким образом

Следовательно, решением заданного уравнения, удовлетворяющим заданным начальным условиям, является функция
 .
.
