
- •СОДЕРЖАНИЕ
- •ВВЕДЕНИЕ
- •ГЛАВА 1. ОРИЕНТИРОВАНИЕ НАБЛЮДАТЕЛЯ НА ЗЕМНОЙ ПОВЕРХНОСТИ
- •1.1. Фигура и размеры Земли
- •Элементы основных референц-эллипсоидов (из табл. 2.23 «МТ-2000»)
- •Дополнительные данные к эллипсоиду Красовского
- •1.2. Основные точки, линии и плоскости на поверхности Земли
- •1.3.1. Географические координаты
- •Географические координаты некоторых портов Мира
- •1.3.2. Разности широт и долгот
- •1.3.3. Задачи на расчет значений (Δφ, Δλ, φ2, λ2)
- •А. Расчет значений разности широт (Δφ) и разности долгот (Δλ)
- •Б. Расчет значений широты (φ2) и долготы (λ2) пункта прихода
- •1.4. Радиусы кривизны земного эллипсоида
- •Выводы
- •ГЛАВА 2. ОПРЕДЕЛЕНИЕ НАПРАВЛЕНИЙ В МОРЕ
- •2.1. Основные линии и плоскости наблюдателя
- •2.2. Системы счета направлений
- •2.2.1. Круговая система счета
- •2.2.2. Полукруговая система счета
- •2.2.3. Четвертная система счета
- •2.2.4. Румбовая система счета (рис. 2.6)
- •2.2.5. Задачи на перевод направлений в круговую систему счета
- •2.3. Истинные направления и их соотношения
- •Б. Расчет значения ИП по известным ИК и КУ
- •В. Расчет значения ИК по известным ИП и КУ
- •2.4. Дальность видимости горизонта и ориентиров в море
- •2.4.1. Дальность видимости горизонта
- •Географическая дальность видимого горизонта (из табл. 2.2. «МТ-75» или 2.1. «МТ-2000»)
- •2.4.2. Дальность видимости ориентиров в море
- •Географическая дальность видимости предметов (из табл. 2.3. «МТ-2000»)
- •2.4.3. Дальность видимости огня ориентира, показанная на карте (рис. 2.16)
- •Б) Открытие огня маяка
- •Выводы
- •ГЛАВА 3. ОПРЕДЕЛЕНИЕ НАПРАВЛЕНИЙ В МОРЕ С ПОМОЩЬЮ МАГНИТНЫХ КОМПАСОВ
- •3.1. Принцип определения направлений по магнитному компасу
- •3.2. Магнитное склонение. Девиация магнитного компаса
- •3.2.1. Магнитное склонение. Магнитные направления
- •3.2.2. Девиация магнитного компаса. Компасные направления.
- •3.3. Поправка магнитного компаса и ее определение
- •Девиация магнитного компаса (учебная)
- •3.4. Расчет истинных направлений по магнитному компасу
- •3.4.1. Перевод и исправление румбов
- •3.4.2. Задачи на приведение магнитного склонения (d) к году плавания и расчета поправки магнитного компаса (ΔМК)
- •(год плавания – 2008 г.; δ − из табл. 3.1)
- •3.4.3. Задачи на перевод и исправление румбов
- •Выводы
- •ГЛАВА 4. ОПРЕДЕЛЕНИЕ НАПРАВЛЕНИЙ В МОРЕ С ПОМОЩЬЮ ГИРОСКОПИЧЕСКИХ КУРСОУКАЗАТЕЛЕЙ
- •4.1. Принцип определения направлений с помощью гирокомпасов и гироазимутов
- •4.2. Расчет истинных направлений по гирокомпасу и гироазимуту
- •4.2.1. Расчет истинных направлений по гирокомпасу
- •4.2.2. Расчет истинных направлений по гироазимуту
- •4.3. Способы определения поправок гироскопических курсоуказателей
- •4.3.1. Общие положения
- •4.3.2. Способы определения мгновенных поправок гирокомпаса
- •4.3.3. Задачи по расчету поправки гироазимута (ΔГА3) на заданное время
- •Выводы
- •ГЛАВА 5. ОПРЕДЕЛЕНИЕ СКОРОСТИ СУДНА И ПРОЙДЕННЫХ ИМ РАССТОЯНИЙ
- •5.1. Единицы длины и скорости, применяемые в судовождении
- •5.1.1. Единицы длины, применяемые в судовождении
- •Некоторые единицы длины:
- •5.1.2. Единицы скорости, применяемые в судовождении
- •Скорость в различных единицах (из табл. 37 «МТ-75», табл. 5.15 «МТ-2000»)
- •5.2. Принципы измерения скорости судна
- •5.3. Определение скорости судна. Поправка и коэффициент лага
- •Соответствие скорости хода частоте вращения движителей и поправке (коэффициенту) лага
- •5.4. Определение пройденного судном расстояния
- •Поправка и коэффициент лага (учебная)
- •Использование специальных таблиц
- •Пройденное по лагу расстояние (из табл. 2.17 «МТ-2000») а) при КЛ < 1 (ΔЛ% – отрицательная)
- •б) при КЛ > 1 (ΔЛ% – положительная)
- •Расстояние по времени и скорости (из табл. 2.15 «МТ-2000»)
- •Время по расстоянию и скорости (из табл. 2.16 «МТ-2000»)
- •а) – пройденного судном расстояния (SОБ) заданной скоростью (VОБ) за назначенное время (t)
- •в) – необходимого времени (t) для прохождения заданного расстояния (S) заданной скоростью (VОБ)
- •д) – значений поправки лага на режиме (ΔЛ%) по результатам испытаний на визуальной мерной линии (3 пробега и расстояние между секущими створами – 3,0 мили)
- •Выводы
- •6.1.1. Морская карта. Требования к ее содержанию и оформлению
- •6.1.2. Масштаб карты
- •6.1.3. Классификация морских карт
- •6.1.4. Требования, предъявляемые к морской навигационной карте
- •6.1.5. Система адмиралтейских номеров морских навигационных карт
- •6.2. Принцип построения проекции Меркатора
- •6.2.1. Картографические проекции и их классификация
- •6.2.2. Меркаторская проекция
- •6.3. Уравнение проекции Меркатора
- •6.4. Единицы длины на карте меркаторской проекции
- •Меридиональные части (выдержка)
- •Длина минуты дуги меридиана и параллели (из табл. 2.29 «МТ-2000»)
- •6.5. Построение меркаторской карты
- •6.6. Решение элементарных задач на морской навигационной карте
- •6.7. Примеры решения задач на МНК (по рис. 6.5)
- •А. Снятие с МНК координат
- •Б. Снятие с МНК расстояний между точками
- •В. Снятие с МНК направлений из точки … в точку…
- •Выводы
- •7.1.1. Общие положения. Элементы счисления
- •7.1.2. Счисление пути судна: определение, назначение, сущность и классификация
- •7.1.3. Требования, предъявляемые к счислению пути судна
- •7.2. Графическое счисление координат судна без учета дрейфа и течения
- •7.2.1. Задачи, решаемые при ручном графическом счислении пути судна
- •7.2.2. Требования к оформлению счисления пути судна на карте
- •7.2.3. Решение основных задач счисления пути судна на карте
- •Рис. 7.3. Способы задания на карте заданной точки
- •7.3. Циркуляция судна и ее графический учет
- •7.3.1. Циркуляция судна и ее элементы
- •7.3.2. Способы определения элементов циркуляции судна
- •Таблица циркуляции (учебная)
- •7.3.3. Графический учет циркуляции при счислении пути судна
- •7.3.4. Примеры решения задач по расчету времени и отсчета лага (Т1/ОЛ1) прибытия судна в заданную точку
- •Выводы
- •ГЛАВА 8. ГРАФИЧЕСКОЕ СЧИСЛЕНИЕ КООРДИНАТ СУДНА С УЧЕТОМ ДРЕЙФА ОТ ВЕТРА И ТЕЧЕНИЯ
- •8.1. Определение дрейфа судна от ветра и его учет при графическом счислении
- •8.1.1. Ветер и его влияние на путь судна
- •8.1.2. Определение угла дрейфа от ветра
- •Таблица углов дрейфа
- •8.1.3. Учет дрейфа от ветра при графическом счислении пути судна
- •8.2. Графическое счисление координат судна с учетом течения
- •8.2.1. Морские течения и их влияние на путь судна
- •8.2.2. Учет течения при графическом счислении пути судна
- •8.3. Совместный учет дрейфа от ветра и течения при графическом счислении пути судна
- •8.4. Примеры решения задач по учету дрейфа от ветра и течения
- •а) расчет значения ПУβ при учете постоянного течения (МНК № 32106 или № 3207)
- •б) расчет значения гирокомпасного курса (ГКК) для задания его рулевому при учете течения (для МНК № 32106 или № 3207)
- •в) расчет значения компасного (по магнитному компасу) курса для задания его рулевому при совместном учете дрейфа от ветра (α) и течения (β)
- •Выводы
- •ГЛАВА 9. МОРСКИЕ НАВИГАЦИОННЫЕ КАРТЫ
- •9.1. Классификация морских карт
- •9.1.1. Классификация морских карт по их назначению (см. табл. 9.2)
- •9.1.2. Классификация морских навигационных карт по их масштабу
- •Характеристика морских навигационных карт
- •Классификация морских карт
- •9.1.3. Требования, предъявляемые к морским картам
- •9.2. Степень доверия к морским навигационным картам
- •9.2.1. Критерии качества морской навигационной карты
- •9.2.2. «Подъем» морской навигационной карты
- •9.2.3. Оценка морской навигационной карты судоводителем
- •9.3. Условные знаки морских карт. Чтение карты
- •Значения некоторых условных знаков морских карт
- •Выводы
- •ГЛАВА 10. КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ ИСПОЛЬЗУЕМЫЕ В НАВИГАЦИИ
- •10.1. Классификация картографических проекций
- •10.2. Поперечная цилиндрическая проекция
- •10.3. Перспективные картографические проекции
- •10.4. Равноугольная картографическая проекция Гаусса
- •10.4.1. Общие положения
- •10.4.2. Планшеты в проекции Гаусса
- •10.4.3. Нумерация топографических карт
- •Координатные зоны и пояса карт в проекции Гаусса (из табл. 2.31 «МТ-2000»)
- •а) Долготные зоны
- •б) Широтные пояса
- •Выводы
- •11.2. Средства и методы навигационного оборудования
- •11.3. Зрительные средства навигационного оборудования
- •11.3.1. Определение и классификация
- •11.3.2. Маяки, знаки и огни
- •11.3.3. Навигационные створы
- •11.4. Радиотехнические средства навигационного оборудования (РТСНО)
- •11.4.1. Береговые радиопеленгаторные станции (БРПС) и радиомаяки
- •11.4.2. Радиолокационные отражатели (РЛО)
- •11.4.3. Радионавигационные системы
- •11.5. Плавучие предостерегательные знаки
- •11.5.1. Плавучие маяки, маячные суда и освещаемые поплавки
- •11.5.2. Буи и вехи
- •Характеристика буев
- •11.6. Звукосигнальные и гидроакустические средства навигационного оборудования
- •11.6.1. Звукосигнальные СНО
- •11.6.2. Гидроакустические СНО
- •Выводы
- •ГЛАВА 12. ОСНОВЫ ОПРЕДЕЛЕНИЯ МЕСТА СУДНА В МОРЕ ПО ВИДИМЫМ НАВИГАЦИОННЫМ ОРИЕНТИРАМ
- •12.1.1. Общие принципы определения места судна в море
- •12.1.2. Навигационные параметры и изолинии
- •1. Навигационная изолиния при измерении расстояний (изостадия)
- •2. Навигационная изолиния при измерении пеленга на ориентир (изопеленга)
- •3. Навигационная изолиния при измерении горизонтального угла между двумя ориентирами (изогона)
- •12.2. Сущность определения места судна по навигационным изолиниям
- •12.3. Приведение навигационных параметров и изолиний к одному месту (моменту)
- •Выводы
- •ГЛАВА 13. ОПРЕДЕЛЕНИЕ МЕСТА СУДНА ПО НАПРАВЛЕНИЯМ НА ВИДИМЫЕ НАВИГАЦИОННЫЕ ОРИЕНТИРЫ
- •13.1. Определение места судна по визуальным пеленгам на береговые ориентиры
- •13.1.1. Определение места судна по пеленгам на три ориентира
- •13.1.2. Определение места по пеленгам на два ориентира
- •13.1.3. Определение места судна способом «крюйс-пеленг»
- •13.2.1. Сущность способа
- •13.2.3. Случай неопределенности
- •13.2.4. Практическое выполнение способа определения места судна по двум горизонтальным углам
- •13.2.5. Задачи на определение места судна по направлениям на видимые навигационные ориентиры:
- •а) – по пеленгам на три ориентира (МНК № 32106 или № 3207)
- •б) – по пеленгам на два ориентира (для МНК № 3207 или № 32106)
- •в) – способом «крюйс-пеленг» (для МНК № 32101)
- •г) – по двум горизонтальным углам трех береговых ориентиров (для МНК № 32106 или 3207)
- •Выводы
- •ГЛАВА 14. ОПРЕДЕЛЕНИЕ МЕСТА СУДНА ПО РАССТОЯНИЯМ ДО ВИДИМЫХ НАВИГАЦИОННЫХ ОРИЕНТИРОВ
- •14.1. Средства и способы определения расстояний до видимых ориентиров
- •14.1.1. Определение расстояний с помощью дальномеров
- •14.1.2. Глазомерная оценка расстояний
- •14.1.3. Расчет расстояния до ориентира по измерению его вертикального угла
- •Наклонение видимого горизонта (табл. 11а «МТ-75» или табл. 3.21 «МТ-2000»)
- •Расстояние по вертикальному углу (из табл. 29 «МТ-75» или табл. 2.7 «МТ-2000»)
- •14.1.4. Измерение расстояний до навигационных ориентиров с помощью технических средств
- •14.2. Определение места судна по расстояниям до навигационных ориентиров
- •14.2.2. Определение места судна по расстояниям до трех ориентиров, измеренных с помощью навигационной РЛС
- •14.2.3. Определение места судна по расстояниям до двух ориентиров
- •14.2.5. Определение места судна по пеленгу и расстоянию до ориентира
- •Методика практического выполнения способа (рис. 14.9).
- •14.2.6. Задачи по расчету расстояния до ориентира по измерению его вертикального угла (а) и определению места судна по данным РЛС (б)
- •а) Расчет расстояния до ориентира по измерению его вертикального угла
- •б) Определение места судна по данным РЛС (МНК № 32106 или МНК № 3207)
- •Выводы
- •ГЛАВА 15. КОМБИНИРОВАННЫЕ И ПРИБЛИЖЕННЫЕ СПОСОБЫ ОПРЕДЕЛЕНИЯ МЕСТА СУДНА
- •15.1. Использование эхолота для определения места судна
- •15.1.1. Измерение глубин эхолотом
- •Поправка глубины, измеренной эхолотом (табл. 34в «МТ-75» или 2.11 «МТ-2000»)
- •15.1.2. Задачи на расчет глубины места по показаниям эхолота
- •15.1.3. Определение места судна по глубинам (общий случай)
- •15.1.4. Определение места судна способом «крюйс-изобата»
- •15.1.5. Определение места судна по навигационной линии положения и глубине, измеренной одновременно (рис. 15.4) и разновременно (рис. 15.5)
- •15.2. Комбинированные способы определения места судна
- •15.2.1. Определение места судна по горизонтальному углу и пеленгу на один из ориентиров
- •15.2.2. Определение места судна по горизонтальному углу и расстоянию до одного из ориентиров, рассчитанному по вертикальному углу
- •15.2.3. Определение места судна по разновременным расстояниям до двух и более ориентиров
- •15.2.4. Определение места судна способом исправленное «крюйс-расстояние»
- •15.2.5. Определение места при следовании судна по створу
- •15.3. Приближенные способы определения места судна
- •15.3.1. Уточнение места судна по изобатам
- •15.3.2. Уточнение места судна по линиям положения, параллельным береговой черте с помощью РЛС
- •15.3.3. Уточнение места судна по моменту открытия маяка и пеленгу на него
- •Выводы
- •ГЛАВА 16. НАВИГАЦИОННЫЕ РУКОВОДСТВА И ПОСОБИЯ ДЛЯ ОБЕСПЕЧЕНИЯ МОРЕПЛАВАНИЯ
- •16.1. Общие сведения. Назначение и классификация
- •16.1.1. Морские навигационные руководства
- •16.1.2. Морские навигационные пособия
- •16.2. Лоции и дополнения к ним
- •16.3. Руководства «Огни и знаки» («Огни»)
- •Описание СНО («Огни и знаки Черного и Азовского морей» № 2217)
- •16.4. Руководство «РТСНО»
- •Из РТСНО Северного Ледовитого и Атлантического океанов (Адм. № 3001) Украина
- •Радиостанции, работающие по запросу для пеленгования (см. Адм. № 3001 с. 158)
- •Радиопеленгаторные станции Из РТСНО Северного Ледовитого и Атлантического океанов (см. Адм. № 3001 с. 179)
- •Радиолокационные маяки-ответчики (Адм. № 3001 с. 258)
- •16.5. Расписания радиопередач для мореплавателей
- •16.5.1. Расписание радиопередач навигационных и гидрометеорологических сообщений для мореплавателей
- •16.5.2. Расписание факсимильных гидрометеорологических передач
- •16.6. Специальные руководства для плавания
- •16.6.2. Радиолокационные описания маршрутов
- •16.6.3. Руководства для захода судов в порты
- •16.6.4. Сводное описание опасных, запретных и ограниченных для плавания районов
- •16.7. Нумерация морских навигационных руководств и пособий
- •Выводы
- •ГЛАВА 17. АНАЛИТИЧЕСКОЕ (ПИСЬМЕННОЕ) СЧИСЛЕНИЕ КООРДИНАТ СУДНА
- •17.1. Сущность и основные формулы аналитического (письменного) счисления
- •Рис. 17.1. Аналитическое (письменное) счисление пути судна
- •17.2. Виды аналитического (письменного) счисления
- •17.2.1. Простое аналитическое (письменное) счисление
- •17.2.2. Составное аналитическое (письменное) счисление
- •17.2.3. Сложное аналитическое (письменное) счисление
- •17.3. Учет дрейфа от ветра, течения и циркуляции судна при аналитическом (письменном) счислении
- •17.4. Понятие об автоматизированном счислении пути судна
- •17.5. Задачи простого аналитического (письменного) счисления пути судна
- •Выводы
- •ГЛАВА 18. ОЦЕНКА И АНАЛИЗ ТОЧНОСТИ СЧИСЛЕНИЯ КООРДИНАТ СУДНА
- •18.2. Оценка точности счисления координат судна
- •Вероятность радиальной погрешности (из табл. 1в «МТ-75» и табл. 4.13 «МТ-2000»)
- •Вероятность радиальной погрешности при круговом распределении мест (из табл. 4.15 «МТ-2000»)
- •18.3. Коэффициент точности счисления и его расчет
- •18.4. Средняя квадратическая погрешность линии положения
- •18.5. Радиальная (круговая) СКП обсервованного места судна
- •18.6. Оценка и анализ точности счислимого места судна
- •18.6.1. Средняя квадратическая и предельная погрешности счислимого места судна
- •18.6.2. Выбор безопасного пути судна с учетом точности его плавания
- •Выводы
- •ГЛАВА 19. ОПРЕДЕЛЕНИЕ МЕСТА СУДНА ПО РАДИОПЕЛЕНГАМ НА КРУГОВЫЕ РАДИОМАЯКИ
- •19.1. Принцип радиопеленгования
- •19.2. Исправление и расчет радиопеленгов
- •19.2.1. Радиодевиация
- •19.2.2. Ортодромическая поправка
- •Ортодромическая поправка направления при малом расстоянии
- •19.3. Определение места судна по радиопеленгам на круговые радиомаяки
- •19.3.1. Последовательность действий при определении места судна по радиопеленгам на КРМ
- •19.4. Прокладка радиопеленга на КРМК, находящийся за рамкой карты
- •Задачи на определение места судна по радиопеленгам на круговые РМ-ки
- •Выводы
- •20.2. Радиопеленгаторные станции
- •Таблица предельных расстояний, при которых можно производить прокладку радиопеленгов без учета ортодромических поправок (в милях)
- •20.3. Радиолокационные маяки-ответчики
- •Радиолокационные маяки-ответчики Черного моря
- •20.4. Комбинированные радиомаяки
- •Таблица для определения расстояния по времени прохождения звука в воде и воздухе
- •20.5. Радиомаяки (на плавучих маяках, створные, автоматические) и аэрорамаяки
- •20.6. Девиационные радиомаяки и УКВ радиомаяки с вращающейся характеристикой направленности
- •Девиационные радиомаяки Черного моря
- •Выводы
- •ГЛАВА 21. ИСПОЛЬЗОВАНИЕ СУДОВЫХ РАДИОЛОКАЦИОННЫХ СТАНЦИЙ ДЛЯ ЦЕЛЕЙ НАВИГАЦИИ
- •21.1. Основные эксплуатационные данные судовой РЛС
- •21.1.1. Общие положения
- •Технические характеристики типовых судовых РЛС
- •21.1.2. Максимальная дальность действия и дальность обнаружения объектов
- •21.1.3. Минимальная дальность действия и мертвая зона РЛС
- •21.1.4. Разрешающая способность РЛС
- •21.1.5. Точность радиолокационного пеленгования
- •21.1.6. Радиолокационная девиация
- •21.1.7. Точность измерения расстояний
- •21.2. Чтение радиолокационного изображения
- •21.2.1. Искажение линии берегов
- •21.2.2. Влияние волнения моря
- •21.2.3. Влияние метеорологических условий
- •21.2.4. Обнаружение льдов
- •21.2.5. Теневые секторы
- •21.2.6. Ложные эхо-сигналы
- •21.3. Определение места судна с помощью РЛС
- •21.3.1. Опознавание береговой черты
- •21.3.2. Определение места судна по расстояниям до нескольких ориентиров
- •21.4. Оценка точности обсервованного места по данным РЛС
- •21.6. Задачи на определение места судна по данным РЛС
- •Выводы
- •22.1.1. Общие положения
- •Характеристика радиоволн
- •22.1.2. Классификация радионавигационных систем
- •22.1.3. Общая характеристика гиперболических РНС
- •22.2. Определение места судна с помощью фазовой РНС средней дальности
- •22.2.1. Фазовый метод радионавигационных определений
- •22.2.2. Принцип работы фазовых РНС
- •22.2.3. Определение места судна по фазовым РНС
- •22.2.4. Оценка точности обсервованного места
- •22.3. Определение места судна с помощью импульсно-фазовых РНС
- •22.3.1. Принцип действия импульсно-фазовой РНС
- •22.3.2. Методы получения обсервованного места судна и оценка его точности
- •Точность определения места
- •22.3.3. Импульсно-фазовая РНС «Лоран-С» (США) и «Чайка» (РФ)
- •Соответствие периода повторения буквенно-цифровому обозначению РНС «Лоран-С»
- •Цепи импульсно-фазовой РНС «Лоран-С» (США) и «Чайка» (РФ)
- •22.3.4. Задачи на определение места судна по гиперболическим РНС
- •Выводы
- •ГЛАВА 23. ГЛОБАЛЬНЫЕ НАВИГАЦИОННЫЕ СПУТНИКОВЫЕ СИСТЕМЫ (ГНСС)
- •23.1. Основные закономерности движения ИСЗ и их орбиты
- •23.1.1. Основные закономерности движения ИСЗ
- •Зависимость периода обращения и скорости ИСЗ от высоты его орбиты
- •23.1.2. Орбиты ИСЗ и их особенности
- •23.2. Особенности навигационного использования ИСЗ (НКА)
- •23.3. Способы радионавигационных определений по НКА
- •23.4. Методы определения места судна по НКА
- •А. Дальномерный метод
- •Б. Псевдодальномерный метод
- •В. Разностно-дальномерный метод (доплеровский интегральный)
- •Г. Радиально-скоростной (доплеровский дифференциальный) метод
- •23.5. Структура глобальных навигационных спутниковых систем
- •А. Общие сведения
- •Б. Подсистема навигационных космических аппаратов
- •В. Подсистема контроля и управления
- •Г. Подсистема навигационной аппаратуры потребителей
- •Д. Информация на дисплее судового приемоиндикатора
- •Е. Сравнительная характеристика ГНСС
- •Сравнительные характеристики GPS (США) и ГЛОНАСС (РФ)
- •Ж. Дифференциальная подсистема ГНСС (ДПС ГНСС)
- •Эксплуатационные требования к морской дифференциальной подсистеме
- •ККС Черного моря (из РТСНО адм. № 3001)
- •З. Точность определения места по среднеорбитальной ГНСС
- •Геометрические факторы в СНС ГЛОНАСС
- •Выводы
- •ГЛАВА 24. ВЕРОЯТНЕЙШЕЕ МЕСТО И РАСЧЕТ БЕЗОПАСНОГО ПУТИ СУДНА
- •24.1. Отыскание вероятнейшего места судна и расчет его точности
- •Какому из этих мест отдать предпочтение и взять за исходное место для дальнейшего счисления пути судна?
- •Задачи на расчет вероятнейшего места судна (для МНК № 3207 или № 32106)
- •24.2. Исключение фигуры погрешностей
- •24.2.1. Общие положения
- •24.2.2. Исключение фигуры погрешностей методом биссектрис
- •24.2.3. Отыскание вероятнейшего места в фигуре погрешностей центрографическим методом
- •24.3. Выбор безопасного пути судна с учетом точности его плавания
- •Коэффициент по заданной вероятности
- •24.4. Расчет периодичности определения места судна для обеспечения заданной точности плавания
- •Задачи на расчет допустимого времени плавания по счислению
- •Периодичность определений места судна (мин.) (допустимое время плавания по счислению)
- •24.5. Рекомендации по анализу счисления пути судна
- •Выводы
- •ГЛАВА 25. СИСТЕМА ОГРАЖДЕНИЯ МАМС И МЕЖДУНАРОДНЫЙ СВОД СИГНАЛОВ
- •25.1. Система ограждения «МАМС»
- •ЛАТЕРАЛЬНЫЕ ЗНАКИ
- •КАРДИНАЛЬНЫЕ ЗНАКИ
- •Условные обозначения характера огня в руководствах для плавання и на картах
- •25.2. Международный свод сигналов (ММС)
- •25.2.1. Общие замечания
- •Значение сигналов предаваемых знаками Морзе флажками (руками):
- •25.2.3. Содержание «МСС-65»
- •Правила пользования сводом (с. 13÷31)
- •Однобуквенные сигналы (с. 35÷41)
- •Общий раздел ММС – 65 (с. 43÷132)
- •Медицинский раздел (с. 133÷167)
- •Приложения (на отдельных вкладных листах)
- •Сигналы о присутствии в районе подводной лодки (в подводном положении)
- •Прием сообщений, касающихся безопасности
- •Указание характера бедствия
- •Сигналы бедствия, предписанные МППСС-72
- •Однобуквенные сигналы, применяемые совместно с цифровыми дополнениями
- •Сигналы, применяемые при всех способах сигнализации
- •Выводы
- •26.1.1. Локсодромия и ее элементы
- •26.1.2. Ортодромия и ее элементы
- •26.2. Основные формулы ортодромии. Способы ее задания
- •26.2.1. Основные формулы ортодромии
- •26.2.2. Способы задания ортодромии
- •26.3. Расчет плавания по локсодромии
- •26.4. Расчет плавания по ортодромии
- •26.4.1. Расчет пройденного по ортодромии расстояния (D)
- •26.4.2. Расчет начального курса плавания по ортодромии (КH)
- •26.4.3. Расчет конечного курса плавания по ортодромии (КK)
- •26.4.4. Расчет значений К0 и λ0
- •26.4.5. Расчет координат промежуточных точек ортодромии
- •26.4.6. Задачи на расчет плавания по ДБК
- •Логарифмы чисел (выдержка из табл. 2 «МТ-75» или табл. 5.44 «МТ-2000»)
- •Меридиональные части (выдержка из табл. 26 «МТ-75» или табл. 2.28а «МТ-2000»)
- •Натуральные значения тригонометрических функций (выдержка из табл. 6-а «МТ-75» или 5.42-а «МТ-2000»)
- •Логарифмы тригонометрических функций (выдержка из табл. 5-а «МТ-75»)
- •Выводы
- •ГЛАВА 27. АНГЛИЙСКИЕ МОРСКИЕ КАРТЫ, РУКОВОДСТВА И ПОСОБИЯ ДЛЯ ПЛАВАНИЯ
- •27.1. Английские морские карты
- •27.1.1. Английские навигационные карты
- •27.1.2. Английские справочные и вспомогательные карты
- •Admiralty Charts and Publications 1608 Approaches Chanakkale bogazi (The Dardanelles)/ Small corrections …. «Depths in meters»
- •27.2. Английские руководства и пособия для плавания
- •Navigational Publications for the professional mariner
- •27.2.1. Английские лоции («Pilots»)
- •«Admiralty List of Lights and For Signals»
- •Содержание каждого тома
- •Выводы
- •ГЛАВА 28. СУДОВАЯ КОЛЛЕКЦИЯ КАРТ, РУКОВОДСТВ И ПОСОБИЙ ДЛЯ ПЛАВАНИЯ
- •28.1. Судовая коллекция карт, руководств и пособий для плавания (СККРиПДП)
- •28.1.1. Комплектование СККРиПДП
- •28.1.2. Хранение, учет, передача и списание карт, руководств и пособий для плавания на судне
- •28.1.3. Каталоги карт и книг
- •28.2. Поддержание карт, руководств и пособий для плавания на уровне современности
- •28.2.1. Общие положения
- •28.2.2. Печатные корректурные документы
- •28.2.3. Навигационные предупреждения, передаваемые по радио
- •28.2.4. Корректурные документы и их хранение на судне
- •28.2.5. Корректура карт, руководств и пособий для плавания на судне
- •Выводы
- •ГЛАВА 29. ПОДГОТОВКА ШТУРМАНСКОЙ ЧАСТИ К РЕЙСУ
- •29.1. Рейсовое задание
- •29.2. Подбор карт, руководств и пособий для плавания на переход
- •А. Карты
- •Б. Руководства и пособия для плавания
- •Классификация руководств и пособий для плавания
- •29.3. Изучение района плавания
- •29.4. Предварительная прокладка пути судна
- •Таблица плавання
- •29.5. Подъем карт и окончательная проработка плана перехода
- •29.5.1. Подъем карт
- •29.5.2. Окончательная проработка плана перехода
- •29.6. Штурманская справка на переход
- •Выводы
- •ГЛАВА 30. ОРГАНИЗАЦИЯ ВАХТЫ НА МОСТИКЕ
- •30.1. Общие принципы организации вахты
- •30.2. Заступление на вахту и ее несение при стоянке судна
- •30.2.1. Обязанности ВПК при стоянке судна в порту
- •30.2.2. Обязанности ВПК при стоянке судна на якоре
- •30.3. Подготовка судна к выходу в море
- •30.4. Прием-сдача ходовой вахты
- •30.5. Наблюдение и вахта на мостике
- •30.6. Определение поправок ТСН
- •30.7. Характерные недостатки технических средств и способов навигации
- •Выводы
- •31.2. Счисление пути судна
- •Условные обозначения для счислимых и обсервованных мест
- •31.3. Определение места судна
- •31.4. Стандарты точности судовождения
- •Международные стандарты точности судовождения
- •Коэффициенты для расчета радиальной погрешности заданной вероятности (для отношения полуосей эллипса погрешностей в/а = 1,0)
- •Международные стандарты точности судовождения
- •Отечественные нормативы точности судовождения
- •31.5. Оценка точности места судна
- •Среднеквадратические погрешности (mU) основных навигационных параметров (из таблицы 4.3. «МТ-2000»)
- •Расчет точности места судна
- •31.6. Маневренные характеристики судна. Лоцманская карточка
- •Лоцманская карточка (из приложения 6 «РШСУ-98»)
- •Характеристика рулевого устройства
- •Проверка наличия на борту и готовности
- •Прочая информация
- •31.7. Правила ведения судового журнала
- •1. Общие положения.
- •2. Порядок заполнения судового журнала.
- •Выводы
- •ГЛАВА 32. НАВИГАЦИОННОЕ ОБЕСПЕЧЕНИЕ ПЛАВАНИЯ В СТЕСНЕННЫХ ВОДАХ
- •32.1. Общая характеристика условий плавания в стесненных водах
- •32.1.1. Основные особенности условий плавания в стесненных водах
- •32.1.2. Безопасная скорость судна
- •Правило 6 «МППСС-72». Безопасная скорость
- •32.2. Подготовка к плаванию в стесненных условиях
- •32.2.1. Навигационные особенности плавания в стесненных условиях
- •Навигационными особенностями плавания в стесненных условиях являются:
- •Специальными мерами, обеспечивающими навигационную безопасность в стесненных водах, являются:
- •32.2.3. Расчет и планирование поворота. Контроль глубин
- •32.2.4. Подготовка к плаванию в стесненных водах
- •Проверочный лист подготовки судна к плаванию в стесненных условиях
- •32.3. Обеспечение навигационной безопасности при плавании в стесненных водах
- •32.3.1. Допустимое расстояние до навигационных опасностей, расположенных по одному борту
- •32.3.2. Допустимое относительное отклонение от оси полосы одностороннего движения
- •32.3.3. Допустимые радиальные СКП места при плавании среди навигационных опасностей
- •32.3.4. Допустимые радиальные СКП места при плавании вблизи навигационных опасностей, расположенных по одному борту
- •32.3.5. Допустимые СКП места по перпендикуляру к оси полосы одностороннего движения
- •32.4. Обязанности судоводителя при плавании в стесненных условиях
- •32.4.1. Обязанности ВПК при плавании судна в стесненных водах
- •32.4.2. Особенности плавания судна по СРД
- •Правило 10 «МППСС-72». Плавание по системам разделения движения
- •32.4.3. Действия ВПК при выходе судна из полосы движения СРД
- •Выводы
- •ГЛАВА 33. НАВИГАЦИОННОЕ ОБЕСПЕЧЕНИЕ ПЛАВАНИЯ СУДНА В ОТКРЫТОМ МОРЕ
- •33.1. Навигационное обеспечение плавания
- •33.1.1. Плавание по наивыгоднейшим путям
- •33.1.2. Оптимальная скорость судна
- •33.1.3. Контроль за местом судна
- •33.2. Судовождение в высоких широтах
- •33.2.1. Навигационные условия плавания
- •33.2.2. Счисление координат судна
- •33.2.3. Особенности определения места судна
- •33.3. Особенности судовождения при плавании в шторм
- •33.3.1. Оценка ветроволновых потерь скорости судна
- •33.3.2. Уклонение от штормовых зон
- •33.3.4. Обязанности судоводителей:
- •Выводы
- •ГЛАВА 34. НАВИГАЦИОННОЕ ОБЕСПЕЧЕНИЕ ПЛАВАНИЯ СУДНА НА МОРЯХ С ПРИЛИВАМИ
- •34.1. Физическая сущность явления приливов и отливов
- •34.2. Основные элементы прилива
- •34.3. Неравенства приливов
- •Суточные (тропические) неравенства
- •Полумесячные (фазовые) неравенства
- •Характеристика прилива по возрасту Луны
- •Параллактические (месячные) неравенства
- •34.4. Таблицы приливов
- •Приливы в основных пунктах (выдержка)
- •Поправки для дополнительных пунктов
- •Поправки высот уровня моря на атмосферное давление
- •34.5. Решение задач с использованием Таблиц приливов
- •Условия индивидуальных задач
- •Задача 2.
- •34.6. График прилива
- •34.7. Предвычисление приливов по гармоническим постоянным
- •34.8. Сведения о приливо-отливных явлениях, помещаемых на картах
- •Негармонические постоянные
- •34.9. Атласы приливо-отливных явлений
- •34.10. Судовождение в морях с приливами
- •Выводы
- •35.1. Подготовка судна к подходу к берегу
- •35.2. Подход судна к берегу с моря
- •35.3. Навигационное обеспечение плавания судна при подходе к побережью
- •35.3.1. Варианты подхода судна к побережью
- •35.3.2. Выбор курсов подхода
- •35.3.3. Опознавание ориентиров
- •35.4. Навигационное обеспечение прибрежного плавания
- •Выводы
- •36.2. Особенности навигационных условий в шхерах
- •36.3. Особенности судовождения в узкостях
- •36.4. Ограждающие и опасные изолинии
- •36.5. Сетки изолиний
- •Выводы
- •37.2. Признаки приближения судна ко льдам, к разводьям и чистой воде
- •37.3 Особенности навигационных условий плавания во льдах
- •37.4 Способы определения скорости хода судна при плавании во льдах
- •37.5. Определение дрейфа судна в сплоченных льдах
- •37.6. Особенности счисления пути судна при плавании во льдах
- •37.7. Действия судоводителей при плавании во льдах
- •Выводы
- •ГЛАВА 38. ОСОБЕННОСТИ СУДОВОЖДЕНИЯ ПО ВВП. ПОСТАНОВКА СУДА НА ЯКОРЬ
- •38.1. Особенности судовождения при плавании по ВВП
- •38.1.1. Основные понятия, определения и термины
- •38.1.2. Особенности навигационных условий ВВП
- •38.1.3. Судоходная обстановка и сигнализация
- •38.1.4. Организация и обеспечение судоходства по ВВП
- •38.1.5. Навигационные пособия
- •38.1.6. Особенности судовождения при плавании по ВВП
- •38.2.Постановка суда на якорь
- •Выводы
- •СИСТЕМА МАМС – РЕГИОН А
- •ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯ, ПРИМЕНЯЕМЫЕ ПРИ ВЕДЕНИИ СУДОВОГО ЖУРНАЛА И РЕШЕНИИ ЗАДАЧ СУДОВОЖДЕНИЯ
- •ПЕРЕЧЕНЬ И ЗНАЧЕНИЕ СОКРАЩЕНИЙ, ИСПОЛЬЗОВАННЫХ В ТЕКСТЕ
- •ПЕРЕЧЕНЬ ЛИТЕРАТУРЫ
Решение: 1) |
Из табл. 18.1 по аргументу Р = 0,866 определяем Z = 1,5. |
2) |
Вычисляем искомые пределы погрешности |
|
υD = 1,5 · 0,5 = ±0,75кб. |
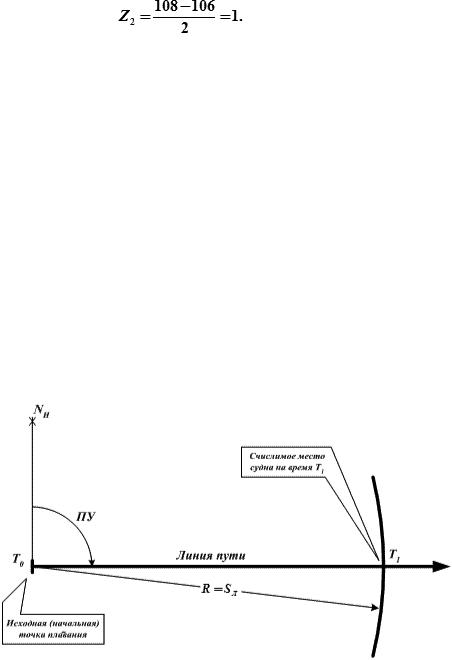
Задача 5: Определить вероятность того, что действительное расстояние до ориентира не выйдет за
пределы 105÷108кб, если среднее арифметическое (вероятнейшее) расстояние до ориентира D = 106кб., а СКП измерения расстояния mD = ±2 кб.
Решение: 1) Рассчитываем аргументы функции Лапласа для случайных величин:
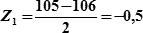 и
и
2)Из табл.18.1 по аргументам Z1 и Z2 выбираем значения вероятностей: Р1 = 0,383 и Р2 = 0,683
3)Вычисляем искомую вероятность Р = 0,5 (0,683 + 0,383) = 0,533. (т.к. «Z1» величина отрицательная, то функции Лапласа складываются).
18.2. Оценка точности счисления координат судна
Современный уровень штурманской техники все еще не позволяет перейти к обсервационному способу судовождения, то есть судовождению на основе непрерывного определения места судна по внешним ориентирам. Поэтому основой выработки текущих (счислимых) координат места судна является счисление его пути, на основе которого получают (графически, аналитически, графоаналитически) текущие координаты (счислимое место судна) на любой момент времени.
Счислимое место судна на любой момент времени определяется точкой пересечения двух линий
(рис. 18.2.):
•линии пути судна;
•дуги окружности, проведенной из исходной точки плавания, радиусом, равным пройденному судном расстоянию.
Рис. 18.2. Счислимое место судна
Врезультате неточного учета (или их изменения со временем) таких элементов, как поправка
курсоуказателя (ΔК), величина угла дрейфа (α°), направление учитываемого течения (КТ) и его скорости (υТ) и пр. – путевой угол (ПУ) будет отличаться от расчетного на некоторую величину (ΔПУ).
Врезультате же неточного учета (или их изменения со временем) таких элементов, как поправка
лага (Δ Л%), скорость учитываемого течения (υТ) и пр. – пройденное судном расстояние (SЛ) будет отличаться от расчетного на некоторую величину (ΔS).
Учтя все погрешности, влияющие на путевой угол и все погрешности, влияющие на пройденное судном расстояние (см. табл. 12.1.), можно получить СКП путевого угла (mПУ) и СКП пройденного судном расстояния (mS).
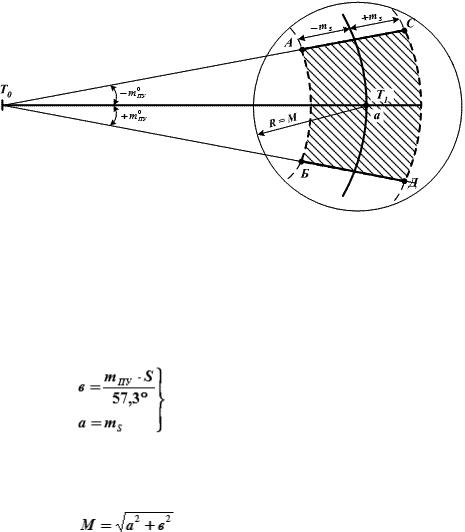
Под воздействием этих погрешностей (mПУ и mS) счислимое место судна на какой-то момент времени Т1 (рис. 18.3) будет располагаться не в конкретной точке (т. а), а в пределах некоторой площади (на рис. 18.3 – заштриховано), но где именно – заранее не известно.
Рис. 18.3. Погрешность счисления пути судна
Это объясняется тем, что величина и знак абсолютного изменения путевого угла ( ПУ) и пройденного расстояния (ΔS) проявляются как случайные величины.
Ссылаясь на теорию погрешности можно оценить вероятность нахождения счислимого места на время Т1 в «заштрихованной» (рис. 18.3) фигуре погрешности величиной Р = 46% (0,46).
Если в эту фигуру вписать эллипс на полуосях
(18.7)
то вероятность нахождения счислимого места на время Т1 в эллипсе оценится в Р ≈ 39% (0,39). → рис.
18.11.
В практике судовождения точность места принято оценивать радиальной или круговой
среднеквадратической погрешностью
(18.8)
Зная значение М из т. а проведем окружность радиусом R = М . Вероятность нахождения счислимого места в круге, радиусом R = M, составит 63÷68% (0,63÷0,68) в зависимости от соотношения полуосей эллипса (а и в).
Как видно из рис. 18.3 величина радиуса R = M будет увеличиваться постоянно с увеличением пройденного судном расстояния (S).
На основании многолетних наблюдений получены следующие приближенные значения радиуса R
=M для нормальных условий плавания в зависимости от пройденного расстояния:
•без ветра и течения: М ≈ 0,02·S → если S = 100 миль, то М = 2 мили;
•с учетом дрейфа от ветра: М ≈ 0,03·S → если S = 100 миль, то М = 3 мили;
•с учетом дрейфа от ветра и течения: М ≈ 0,03÷0,07·S → если S = 100 миль, то М = 3÷7 миль.
Для конкретного проекта (типа) судна для конкретного района плавания (Черное море, Средиземное море и др.) нужно знать значение радиальной СКП счисления (МС), чтобы иметь возможность в любое время оценить навигационную безопасность плавания.
Величина МС зависит от пройденного судном расстояния, то есть от времени плавания по счислению. Осталось выяснить «скорость» увеличения МС, то есть знать величину – коэффициента точности счисления (КС).

Вероятность радиальной погрешности (из табл. 1в «МТ-75» и табл. 4.13 «МТ-2000»)
Таблица 18.2.
КР = |
|
|
Отношение полуосей эллипса погрешностей е = в/а |
|
|
||||||
0,0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
0,080 |
0,045 |
0,025 |
0,018 |
0,014 |
0,012 |
0,011 |
0,011 |
0,010 |
0,010 |
0,010 |
0,2 |
159 |
135 |
092 |
068 |
056 |
048 |
044 |
042 |
040 |
039 |
039 |
0,3 |
236 |
223 |
179 |
142 |
119 |
105 |
096 |
091 |
088 |
086 |
086 |
0,4 |
311 |
303 |
270 |
229 |
198 |
177 |
164 |
156 |
151 |
149 |
148 |
0,5 |
383 |
377 |
356 |
319 |
285 |
260 |
243 |
232 |
225 |
222 |
221 |
0,6 |
452 |
448 |
434 |
406 |
374 |
347 |
328 |
315 |
307 |
304 |
302 |
0,7 |
516 |
514 |
505 |
486 |
459 |
434 |
415 |
401 |
393 |
389 |
387 |
0,8 |
576 |
575 |
570 |
558 |
539 |
517 |
499 |
487 |
478 |
474 |
473 |
0,9 |
632 |
631 |
629 |
623 |
610 |
594 |
579 |
568 |
560 |
556 |
555 |
1,0 |
0,683 |
0,683 |
0,682 |
0,680 |
0,674 |
0,663 |
0,652 |
0,643 |
0,636 |
0,633 |
0,632 |
1,1 |
729 |
729 |
730 |
731 |
729 |
723 |
716 |
710 |
705 |
703 |
702 |
1,2 |
770 |
771 |
772 |
775 |
776 |
775 |
772 |
768 |
765 |
764 |
763 |
1,3 |
806 |
807 |
810 |
814 |
817 |
819 |
819 |
818 |
817 |
816 |
815 |
1,4 |
838 |
840 |
842 |
847 |
852 |
856 |
858 |
859 |
859 |
859 |
859 |
1,5 |
866 |
868 |
870 |
875 |
881 |
886 |
890 |
892 |
894 |
894 |
895 |
1,6 |
890 |
891 |
895 |
899 |
905 |
911 |
916 |
919 |
921 |
922 |
923 |
1,7 |
911 |
912 |
915 |
919 |
925 |
931 |
936 |
940 |
943 |
944 |
944 |
1,8 |
928 |
929 |
932 |
936 |
942 |
947 |
952 |
956 |
959 |
960 |
961 |
1,9 |
943 |
944 |
946 |
950 |
955 |
960 |
965 |
968 |
971 |
972 |
973 |
2,0 |
0,954 |
0,955 |
0,958 |
0,961 |
0,965 |
0,970 |
0,974 |
0,978 |
0,980 |
0,981 |
0,982 |
2,1 |
964 |
965 |
967 |
970 |
974 |
978 |
981 |
984 |
986 |
987 |
988 |
2,2 |
972 |
973 |
975 |
977 |
980 |
984 |
987 |
989 |
991 |
992 |
992 |
2,3 |
979 |
979 |
981 |
983 |
985 |
988 |
990 |
992 |
994 |
995 |
995 |
2,4 |
984 |
984 |
985 |
987 |
989 |
991 |
993 |
995 |
996 |
997 |
997 |
2,5 |
988 |
988 |
989 |
990 |
992 |
994 |
995 |
997 |
998 |
998 |
998 |
2,6 |
991 |
991 |
992 |
993 |
994 |
996 |
997 |
998 |
998 |
999 |
999 |
2,7 |
993 |
993 |
994 |
995 |
996 |
997 |
998 |
999 |
999 |
999 |
999 |
2,8 |
995 |
995 |
996 |
996 |
997 |
998 |
999 |
999 |
999 |
999 |
1,000 |
2,9 |
996 |
996 |
997 |
997 |
998 |
999 |
999 |
999 |
1,000 |
1,000 |
1,000 |
3,0 |
0,997 |
0,997 |
0,998 |
0,998 |
0,999 |
0,999 |
0,999 |
1,000 |
1,000 |
1,000 |
1,000 |
КР = RР / М → коэффициент (нормированная радиальная погрешность), равный заданной радиальной погрешности (RР) в долях радиальной СКП места (М).
Если «а» и «в» неизвестны, то выборки по в/а = 1.
Задача: Определить вероятность нахождения места судна в круге радиуса 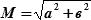 и круге радиуса RР = 2,9 мили, если полуоси эллипса погрешностей: а = 1,8 мили, в = 0,7 мили.
и круге радиуса RР = 2,9 мили, если полуоси эллипса погрешностей: а = 1,8 мили, в = 0,7 мили.
Решение: 1) рассчитываем отношение полуосей эллипса: e = b/a = 0,7/1,8 = 0,4.
2)вычисляем радиальную СКП места судна:
3)из табл. 18.2 по КР = 1 (для радиальной СКП RР = М) и е = 0,4 выбираем Р = 0,674 (67,4%)
4)из табл. 18.2 по 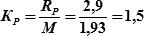 и е = 0,4 выбираем Р = 0,881 (88,1%).
и е = 0,4 выбираем Р = 0,881 (88,1%).

Вероятность радиальной погрешности при круговом распределении мест (из табл. 4.15 «МТ-2000»)
Таблица 18.3.
КР = |
0,00 |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
0,010 |
0,012 |
0,014 |
0,017 |
0,019 |
0,022 |
0,025 |
0,028 |
0,032 |
0,035 |
0,2 |
039 |
043 |
047 |
052 |
056 |
061 |
065 |
070 |
075 |
081 |
0,3 |
086 |
092 |
097 |
103 |
109 |
115 |
122 |
128 |
134 |
141 |
0,4 |
148 |
155 |
162 |
169 |
176 |
183 |
191 |
198 |
206 |
213 |
0,5 |
221 |
229 |
237 |
245 |
253 |
261 |
269 |
277 |
286 |
294 |
0,6 |
302 |
311 |
319 |
328 |
336 |
345 |
353 |
362 |
370 |
379 |
0,7 |
387 |
396 |
405 |
413 |
422 |
430 |
439 |
447 |
456 |
464 |
0,8 |
473 |
481 |
490 |
499 |
506 |
514 |
523 |
531 |
539 |
547 |
0,9 |
555 |
563 |
571 |
579 |
587 |
594 |
602 |
610 |
617 |
625 |
1,0 |
0,632 |
0,639 |
0,647 |
0,654 |
0,661 |
0,668 |
0,675 |
0,682 |
0,689 |
0,695 |
1,1 |
702 |
708 |
715 |
721 |
727 |
734 |
740 |
746 |
752 |
757 |
1,2 |
763 |
769 |
774 |
780 |
785 |
790 |
796 |
801 |
806 |
811 |
1,3 |
815 |
820 |
825 |
829 |
834 |
838 |
843 |
847 |
851 |
855 |
1,4 |
859 |
863 |
867 |
871 |
874 |
878 |
881 |
885 |
888 |
891 |
1,5 |
895 |
898 |
901 |
904 |
907 |
910 |
912 |
915 |
918 |
920 |
1,6 |
923 |
925 |
928 |
930 |
932 |
934 |
936 |
939 |
941 |
943 |
1,7 |
944 |
946 |
948 |
950 |
952 |
953 |
955 |
956 |
958 |
959 |
1,8 |
961 |
962 |
964 |
965 |
966 |
968 |
969 |
970 |
971 |
972 |
1,9 |
973 |
974 |
975 |
976 |
977 |
978 |
979 |
979 |
980 |
981 |
2,0 |
0,982 |
0,982 |
0,983 |
0,984 |
0,984 |
0,985 |
0,986 |
0,986 |
0,987 |
0,987 |
2,1 |
988 |
988 |
989 |
989 |
990 |
990 |
991 |
991 |
991 |
992 |
2,2 |
992 |
992 |
993 |
993 |
993 |
994 |
994 |
994 |
994 |
995 |
2,3 |
995 |
995 |
995 |
996 |
996 |
996 |
996 |
996 |
997 |
997 |
2,4 |
997 |
997 |
997 |
997 |
997 |
998 |
998 |
998 |
998 |
998 |
2,5 |
998 |
998 |
998 |
998 |
998 |
998 |
999 |
999 |
999 |
999 |
2,6 |
999 |
999 |
999 |
999 |
999 |
999 |
999 |
999 |
999 |
999 |
2,7 |
999 |
999 |
999 |
999 |
999 |
999 |
1,000 |
1,000 |
1,000 |
1,000 |
2,8 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
КР = 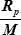 – отношение заданной радиальной погрешности (RР) к радиальной СКП места (М) при b/a =
– отношение заданной радиальной погрешности (RР) к радиальной СКП места (М) при b/a =
1.
Задача 1: Определить вероятность нахождения действительного места судна в круге радиуса RР = 1,2
мили, если радиальная СКП при круговом распределении мест судна М = 0,6 мили.
Решение: |
|
из табл. 18.3 по коэффициенту |
выбираем значение Р = 0,982 (98,2%). |
Задача 2: Определить радиальную погрешность для вероятности Рзад = 0,95 (95%), если радиальная
СКП при круговом распределении мест судна М = 0,8 мили.
Решение: из табл. 18.3 по Рзад = 0,95 (95%) выбираем КР = 1,73 следовательно: R0,95 = 1,73 · 0,8 мили =
1,4 мили.
