
- •СОДЕРЖАНИЕ
- •ВВЕДЕНИЕ
- •ГЛАВА 1. ОРИЕНТИРОВАНИЕ НАБЛЮДАТЕЛЯ НА ЗЕМНОЙ ПОВЕРХНОСТИ
- •1.1. Фигура и размеры Земли
- •Элементы основных референц-эллипсоидов (из табл. 2.23 «МТ-2000»)
- •Дополнительные данные к эллипсоиду Красовского
- •1.2. Основные точки, линии и плоскости на поверхности Земли
- •1.3.1. Географические координаты
- •Географические координаты некоторых портов Мира
- •1.3.2. Разности широт и долгот
- •1.3.3. Задачи на расчет значений (Δφ, Δλ, φ2, λ2)
- •А. Расчет значений разности широт (Δφ) и разности долгот (Δλ)
- •Б. Расчет значений широты (φ2) и долготы (λ2) пункта прихода
- •1.4. Радиусы кривизны земного эллипсоида
- •Выводы
- •ГЛАВА 2. ОПРЕДЕЛЕНИЕ НАПРАВЛЕНИЙ В МОРЕ
- •2.1. Основные линии и плоскости наблюдателя
- •2.2. Системы счета направлений
- •2.2.1. Круговая система счета
- •2.2.2. Полукруговая система счета
- •2.2.3. Четвертная система счета
- •2.2.4. Румбовая система счета (рис. 2.6)
- •2.2.5. Задачи на перевод направлений в круговую систему счета
- •2.3. Истинные направления и их соотношения
- •Б. Расчет значения ИП по известным ИК и КУ
- •В. Расчет значения ИК по известным ИП и КУ
- •2.4. Дальность видимости горизонта и ориентиров в море
- •2.4.1. Дальность видимости горизонта
- •Географическая дальность видимого горизонта (из табл. 2.2. «МТ-75» или 2.1. «МТ-2000»)
- •2.4.2. Дальность видимости ориентиров в море
- •Географическая дальность видимости предметов (из табл. 2.3. «МТ-2000»)
- •2.4.3. Дальность видимости огня ориентира, показанная на карте (рис. 2.16)
- •Б) Открытие огня маяка
- •Выводы
- •ГЛАВА 3. ОПРЕДЕЛЕНИЕ НАПРАВЛЕНИЙ В МОРЕ С ПОМОЩЬЮ МАГНИТНЫХ КОМПАСОВ
- •3.1. Принцип определения направлений по магнитному компасу
- •3.2. Магнитное склонение. Девиация магнитного компаса
- •3.2.1. Магнитное склонение. Магнитные направления
- •3.2.2. Девиация магнитного компаса. Компасные направления.
- •3.3. Поправка магнитного компаса и ее определение
- •Девиация магнитного компаса (учебная)
- •3.4. Расчет истинных направлений по магнитному компасу
- •3.4.1. Перевод и исправление румбов
- •3.4.2. Задачи на приведение магнитного склонения (d) к году плавания и расчета поправки магнитного компаса (ΔМК)
- •(год плавания – 2008 г.; δ − из табл. 3.1)
- •3.4.3. Задачи на перевод и исправление румбов
- •Выводы
- •ГЛАВА 4. ОПРЕДЕЛЕНИЕ НАПРАВЛЕНИЙ В МОРЕ С ПОМОЩЬЮ ГИРОСКОПИЧЕСКИХ КУРСОУКАЗАТЕЛЕЙ
- •4.1. Принцип определения направлений с помощью гирокомпасов и гироазимутов
- •4.2. Расчет истинных направлений по гирокомпасу и гироазимуту
- •4.2.1. Расчет истинных направлений по гирокомпасу
- •4.2.2. Расчет истинных направлений по гироазимуту
- •4.3. Способы определения поправок гироскопических курсоуказателей
- •4.3.1. Общие положения
- •4.3.2. Способы определения мгновенных поправок гирокомпаса
- •4.3.3. Задачи по расчету поправки гироазимута (ΔГА3) на заданное время
- •Выводы
- •ГЛАВА 5. ОПРЕДЕЛЕНИЕ СКОРОСТИ СУДНА И ПРОЙДЕННЫХ ИМ РАССТОЯНИЙ
- •5.1. Единицы длины и скорости, применяемые в судовождении
- •5.1.1. Единицы длины, применяемые в судовождении
- •Некоторые единицы длины:
- •5.1.2. Единицы скорости, применяемые в судовождении
- •Скорость в различных единицах (из табл. 37 «МТ-75», табл. 5.15 «МТ-2000»)
- •5.2. Принципы измерения скорости судна
- •5.3. Определение скорости судна. Поправка и коэффициент лага
- •Соответствие скорости хода частоте вращения движителей и поправке (коэффициенту) лага
- •5.4. Определение пройденного судном расстояния
- •Поправка и коэффициент лага (учебная)
- •Использование специальных таблиц
- •Пройденное по лагу расстояние (из табл. 2.17 «МТ-2000») а) при КЛ < 1 (ΔЛ% – отрицательная)
- •б) при КЛ > 1 (ΔЛ% – положительная)
- •Расстояние по времени и скорости (из табл. 2.15 «МТ-2000»)
- •Время по расстоянию и скорости (из табл. 2.16 «МТ-2000»)
- •а) – пройденного судном расстояния (SОБ) заданной скоростью (VОБ) за назначенное время (t)
- •в) – необходимого времени (t) для прохождения заданного расстояния (S) заданной скоростью (VОБ)
- •д) – значений поправки лага на режиме (ΔЛ%) по результатам испытаний на визуальной мерной линии (3 пробега и расстояние между секущими створами – 3,0 мили)
- •Выводы
- •6.1.1. Морская карта. Требования к ее содержанию и оформлению
- •6.1.2. Масштаб карты
- •6.1.3. Классификация морских карт
- •6.1.4. Требования, предъявляемые к морской навигационной карте
- •6.1.5. Система адмиралтейских номеров морских навигационных карт
- •6.2. Принцип построения проекции Меркатора
- •6.2.1. Картографические проекции и их классификация
- •6.2.2. Меркаторская проекция
- •6.3. Уравнение проекции Меркатора
- •6.4. Единицы длины на карте меркаторской проекции
- •Меридиональные части (выдержка)
- •Длина минуты дуги меридиана и параллели (из табл. 2.29 «МТ-2000»)
- •6.5. Построение меркаторской карты
- •6.6. Решение элементарных задач на морской навигационной карте
- •6.7. Примеры решения задач на МНК (по рис. 6.5)
- •А. Снятие с МНК координат
- •Б. Снятие с МНК расстояний между точками
- •В. Снятие с МНК направлений из точки … в точку…
- •Выводы
- •7.1.1. Общие положения. Элементы счисления
- •7.1.2. Счисление пути судна: определение, назначение, сущность и классификация
- •7.1.3. Требования, предъявляемые к счислению пути судна
- •7.2. Графическое счисление координат судна без учета дрейфа и течения
- •7.2.1. Задачи, решаемые при ручном графическом счислении пути судна
- •7.2.2. Требования к оформлению счисления пути судна на карте
- •7.2.3. Решение основных задач счисления пути судна на карте
- •Рис. 7.3. Способы задания на карте заданной точки
- •7.3. Циркуляция судна и ее графический учет
- •7.3.1. Циркуляция судна и ее элементы
- •7.3.2. Способы определения элементов циркуляции судна
- •Таблица циркуляции (учебная)
- •7.3.3. Графический учет циркуляции при счислении пути судна
- •7.3.4. Примеры решения задач по расчету времени и отсчета лага (Т1/ОЛ1) прибытия судна в заданную точку
- •Выводы
- •ГЛАВА 8. ГРАФИЧЕСКОЕ СЧИСЛЕНИЕ КООРДИНАТ СУДНА С УЧЕТОМ ДРЕЙФА ОТ ВЕТРА И ТЕЧЕНИЯ
- •8.1. Определение дрейфа судна от ветра и его учет при графическом счислении
- •8.1.1. Ветер и его влияние на путь судна
- •8.1.2. Определение угла дрейфа от ветра
- •Таблица углов дрейфа
- •8.1.3. Учет дрейфа от ветра при графическом счислении пути судна
- •8.2. Графическое счисление координат судна с учетом течения
- •8.2.1. Морские течения и их влияние на путь судна
- •8.2.2. Учет течения при графическом счислении пути судна
- •8.3. Совместный учет дрейфа от ветра и течения при графическом счислении пути судна
- •8.4. Примеры решения задач по учету дрейфа от ветра и течения
- •а) расчет значения ПУβ при учете постоянного течения (МНК № 32106 или № 3207)
- •б) расчет значения гирокомпасного курса (ГКК) для задания его рулевому при учете течения (для МНК № 32106 или № 3207)
- •в) расчет значения компасного (по магнитному компасу) курса для задания его рулевому при совместном учете дрейфа от ветра (α) и течения (β)
- •Выводы
- •ГЛАВА 9. МОРСКИЕ НАВИГАЦИОННЫЕ КАРТЫ
- •9.1. Классификация морских карт
- •9.1.1. Классификация морских карт по их назначению (см. табл. 9.2)
- •9.1.2. Классификация морских навигационных карт по их масштабу
- •Характеристика морских навигационных карт
- •Классификация морских карт
- •9.1.3. Требования, предъявляемые к морским картам
- •9.2. Степень доверия к морским навигационным картам
- •9.2.1. Критерии качества морской навигационной карты
- •9.2.2. «Подъем» морской навигационной карты
- •9.2.3. Оценка морской навигационной карты судоводителем
- •9.3. Условные знаки морских карт. Чтение карты
- •Значения некоторых условных знаков морских карт
- •Выводы
- •ГЛАВА 10. КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ ИСПОЛЬЗУЕМЫЕ В НАВИГАЦИИ
- •10.1. Классификация картографических проекций
- •10.2. Поперечная цилиндрическая проекция
- •10.3. Перспективные картографические проекции
- •10.4. Равноугольная картографическая проекция Гаусса
- •10.4.1. Общие положения
- •10.4.2. Планшеты в проекции Гаусса
- •10.4.3. Нумерация топографических карт
- •Координатные зоны и пояса карт в проекции Гаусса (из табл. 2.31 «МТ-2000»)
- •а) Долготные зоны
- •б) Широтные пояса
- •Выводы
- •11.2. Средства и методы навигационного оборудования
- •11.3. Зрительные средства навигационного оборудования
- •11.3.1. Определение и классификация
- •11.3.2. Маяки, знаки и огни
- •11.3.3. Навигационные створы
- •11.4. Радиотехнические средства навигационного оборудования (РТСНО)
- •11.4.1. Береговые радиопеленгаторные станции (БРПС) и радиомаяки
- •11.4.2. Радиолокационные отражатели (РЛО)
- •11.4.3. Радионавигационные системы
- •11.5. Плавучие предостерегательные знаки
- •11.5.1. Плавучие маяки, маячные суда и освещаемые поплавки
- •11.5.2. Буи и вехи
- •Характеристика буев
- •11.6. Звукосигнальные и гидроакустические средства навигационного оборудования
- •11.6.1. Звукосигнальные СНО
- •11.6.2. Гидроакустические СНО
- •Выводы
- •ГЛАВА 12. ОСНОВЫ ОПРЕДЕЛЕНИЯ МЕСТА СУДНА В МОРЕ ПО ВИДИМЫМ НАВИГАЦИОННЫМ ОРИЕНТИРАМ
- •12.1.1. Общие принципы определения места судна в море
- •12.1.2. Навигационные параметры и изолинии
- •1. Навигационная изолиния при измерении расстояний (изостадия)
- •2. Навигационная изолиния при измерении пеленга на ориентир (изопеленга)
- •3. Навигационная изолиния при измерении горизонтального угла между двумя ориентирами (изогона)
- •12.2. Сущность определения места судна по навигационным изолиниям
- •12.3. Приведение навигационных параметров и изолиний к одному месту (моменту)
- •Выводы
- •ГЛАВА 13. ОПРЕДЕЛЕНИЕ МЕСТА СУДНА ПО НАПРАВЛЕНИЯМ НА ВИДИМЫЕ НАВИГАЦИОННЫЕ ОРИЕНТИРЫ
- •13.1. Определение места судна по визуальным пеленгам на береговые ориентиры
- •13.1.1. Определение места судна по пеленгам на три ориентира
- •13.1.2. Определение места по пеленгам на два ориентира
- •13.1.3. Определение места судна способом «крюйс-пеленг»
- •13.2.1. Сущность способа
- •13.2.3. Случай неопределенности
- •13.2.4. Практическое выполнение способа определения места судна по двум горизонтальным углам
- •13.2.5. Задачи на определение места судна по направлениям на видимые навигационные ориентиры:
- •а) – по пеленгам на три ориентира (МНК № 32106 или № 3207)
- •б) – по пеленгам на два ориентира (для МНК № 3207 или № 32106)
- •в) – способом «крюйс-пеленг» (для МНК № 32101)
- •г) – по двум горизонтальным углам трех береговых ориентиров (для МНК № 32106 или 3207)
- •Выводы
- •ГЛАВА 14. ОПРЕДЕЛЕНИЕ МЕСТА СУДНА ПО РАССТОЯНИЯМ ДО ВИДИМЫХ НАВИГАЦИОННЫХ ОРИЕНТИРОВ
- •14.1. Средства и способы определения расстояний до видимых ориентиров
- •14.1.1. Определение расстояний с помощью дальномеров
- •14.1.2. Глазомерная оценка расстояний
- •14.1.3. Расчет расстояния до ориентира по измерению его вертикального угла
- •Наклонение видимого горизонта (табл. 11а «МТ-75» или табл. 3.21 «МТ-2000»)
- •Расстояние по вертикальному углу (из табл. 29 «МТ-75» или табл. 2.7 «МТ-2000»)
- •14.1.4. Измерение расстояний до навигационных ориентиров с помощью технических средств
- •14.2. Определение места судна по расстояниям до навигационных ориентиров
- •14.2.2. Определение места судна по расстояниям до трех ориентиров, измеренных с помощью навигационной РЛС
- •14.2.3. Определение места судна по расстояниям до двух ориентиров
- •14.2.5. Определение места судна по пеленгу и расстоянию до ориентира
- •Методика практического выполнения способа (рис. 14.9).
- •14.2.6. Задачи по расчету расстояния до ориентира по измерению его вертикального угла (а) и определению места судна по данным РЛС (б)
- •а) Расчет расстояния до ориентира по измерению его вертикального угла
- •б) Определение места судна по данным РЛС (МНК № 32106 или МНК № 3207)
- •Выводы
- •ГЛАВА 15. КОМБИНИРОВАННЫЕ И ПРИБЛИЖЕННЫЕ СПОСОБЫ ОПРЕДЕЛЕНИЯ МЕСТА СУДНА
- •15.1. Использование эхолота для определения места судна
- •15.1.1. Измерение глубин эхолотом
- •Поправка глубины, измеренной эхолотом (табл. 34в «МТ-75» или 2.11 «МТ-2000»)
- •15.1.2. Задачи на расчет глубины места по показаниям эхолота
- •15.1.3. Определение места судна по глубинам (общий случай)
- •15.1.4. Определение места судна способом «крюйс-изобата»
- •15.1.5. Определение места судна по навигационной линии положения и глубине, измеренной одновременно (рис. 15.4) и разновременно (рис. 15.5)
- •15.2. Комбинированные способы определения места судна
- •15.2.1. Определение места судна по горизонтальному углу и пеленгу на один из ориентиров
- •15.2.2. Определение места судна по горизонтальному углу и расстоянию до одного из ориентиров, рассчитанному по вертикальному углу
- •15.2.3. Определение места судна по разновременным расстояниям до двух и более ориентиров
- •15.2.4. Определение места судна способом исправленное «крюйс-расстояние»
- •15.2.5. Определение места при следовании судна по створу
- •15.3. Приближенные способы определения места судна
- •15.3.1. Уточнение места судна по изобатам
- •15.3.2. Уточнение места судна по линиям положения, параллельным береговой черте с помощью РЛС
- •15.3.3. Уточнение места судна по моменту открытия маяка и пеленгу на него
- •Выводы
- •ГЛАВА 16. НАВИГАЦИОННЫЕ РУКОВОДСТВА И ПОСОБИЯ ДЛЯ ОБЕСПЕЧЕНИЯ МОРЕПЛАВАНИЯ
- •16.1. Общие сведения. Назначение и классификация
- •16.1.1. Морские навигационные руководства
- •16.1.2. Морские навигационные пособия
- •16.2. Лоции и дополнения к ним
- •16.3. Руководства «Огни и знаки» («Огни»)
- •Описание СНО («Огни и знаки Черного и Азовского морей» № 2217)
- •16.4. Руководство «РТСНО»
- •Из РТСНО Северного Ледовитого и Атлантического океанов (Адм. № 3001) Украина
- •Радиостанции, работающие по запросу для пеленгования (см. Адм. № 3001 с. 158)
- •Радиопеленгаторные станции Из РТСНО Северного Ледовитого и Атлантического океанов (см. Адм. № 3001 с. 179)
- •Радиолокационные маяки-ответчики (Адм. № 3001 с. 258)
- •16.5. Расписания радиопередач для мореплавателей
- •16.5.1. Расписание радиопередач навигационных и гидрометеорологических сообщений для мореплавателей
- •16.5.2. Расписание факсимильных гидрометеорологических передач
- •16.6. Специальные руководства для плавания
- •16.6.2. Радиолокационные описания маршрутов
- •16.6.3. Руководства для захода судов в порты
- •16.6.4. Сводное описание опасных, запретных и ограниченных для плавания районов
- •16.7. Нумерация морских навигационных руководств и пособий
- •Выводы
- •ГЛАВА 17. АНАЛИТИЧЕСКОЕ (ПИСЬМЕННОЕ) СЧИСЛЕНИЕ КООРДИНАТ СУДНА
- •17.1. Сущность и основные формулы аналитического (письменного) счисления
- •Рис. 17.1. Аналитическое (письменное) счисление пути судна
- •17.2. Виды аналитического (письменного) счисления
- •17.2.1. Простое аналитическое (письменное) счисление
- •17.2.2. Составное аналитическое (письменное) счисление
- •17.2.3. Сложное аналитическое (письменное) счисление
- •17.3. Учет дрейфа от ветра, течения и циркуляции судна при аналитическом (письменном) счислении
- •17.4. Понятие об автоматизированном счислении пути судна
- •17.5. Задачи простого аналитического (письменного) счисления пути судна
- •Выводы
- •ГЛАВА 18. ОЦЕНКА И АНАЛИЗ ТОЧНОСТИ СЧИСЛЕНИЯ КООРДИНАТ СУДНА
- •18.2. Оценка точности счисления координат судна
- •Вероятность радиальной погрешности (из табл. 1в «МТ-75» и табл. 4.13 «МТ-2000»)
- •Вероятность радиальной погрешности при круговом распределении мест (из табл. 4.15 «МТ-2000»)
- •18.3. Коэффициент точности счисления и его расчет
- •18.4. Средняя квадратическая погрешность линии положения
- •18.5. Радиальная (круговая) СКП обсервованного места судна
- •18.6. Оценка и анализ точности счислимого места судна
- •18.6.1. Средняя квадратическая и предельная погрешности счислимого места судна
- •18.6.2. Выбор безопасного пути судна с учетом точности его плавания
- •Выводы
- •ГЛАВА 19. ОПРЕДЕЛЕНИЕ МЕСТА СУДНА ПО РАДИОПЕЛЕНГАМ НА КРУГОВЫЕ РАДИОМАЯКИ
- •19.1. Принцип радиопеленгования
- •19.2. Исправление и расчет радиопеленгов
- •19.2.1. Радиодевиация
- •19.2.2. Ортодромическая поправка
- •Ортодромическая поправка направления при малом расстоянии
- •19.3. Определение места судна по радиопеленгам на круговые радиомаяки
- •19.3.1. Последовательность действий при определении места судна по радиопеленгам на КРМ
- •19.4. Прокладка радиопеленга на КРМК, находящийся за рамкой карты
- •Задачи на определение места судна по радиопеленгам на круговые РМ-ки
- •Выводы
- •20.2. Радиопеленгаторные станции
- •Таблица предельных расстояний, при которых можно производить прокладку радиопеленгов без учета ортодромических поправок (в милях)
- •20.3. Радиолокационные маяки-ответчики
- •Радиолокационные маяки-ответчики Черного моря
- •20.4. Комбинированные радиомаяки
- •Таблица для определения расстояния по времени прохождения звука в воде и воздухе
- •20.5. Радиомаяки (на плавучих маяках, створные, автоматические) и аэрорамаяки
- •20.6. Девиационные радиомаяки и УКВ радиомаяки с вращающейся характеристикой направленности
- •Девиационные радиомаяки Черного моря
- •Выводы
- •ГЛАВА 21. ИСПОЛЬЗОВАНИЕ СУДОВЫХ РАДИОЛОКАЦИОННЫХ СТАНЦИЙ ДЛЯ ЦЕЛЕЙ НАВИГАЦИИ
- •21.1. Основные эксплуатационные данные судовой РЛС
- •21.1.1. Общие положения
- •Технические характеристики типовых судовых РЛС
- •21.1.2. Максимальная дальность действия и дальность обнаружения объектов
- •21.1.3. Минимальная дальность действия и мертвая зона РЛС
- •21.1.4. Разрешающая способность РЛС
- •21.1.5. Точность радиолокационного пеленгования
- •21.1.6. Радиолокационная девиация
- •21.1.7. Точность измерения расстояний
- •21.2. Чтение радиолокационного изображения
- •21.2.1. Искажение линии берегов
- •21.2.2. Влияние волнения моря
- •21.2.3. Влияние метеорологических условий
- •21.2.4. Обнаружение льдов
- •21.2.5. Теневые секторы
- •21.2.6. Ложные эхо-сигналы
- •21.3. Определение места судна с помощью РЛС
- •21.3.1. Опознавание береговой черты
- •21.3.2. Определение места судна по расстояниям до нескольких ориентиров
- •21.4. Оценка точности обсервованного места по данным РЛС
- •21.6. Задачи на определение места судна по данным РЛС
- •Выводы
- •22.1.1. Общие положения
- •Характеристика радиоволн
- •22.1.2. Классификация радионавигационных систем
- •22.1.3. Общая характеристика гиперболических РНС
- •22.2. Определение места судна с помощью фазовой РНС средней дальности
- •22.2.1. Фазовый метод радионавигационных определений
- •22.2.2. Принцип работы фазовых РНС
- •22.2.3. Определение места судна по фазовым РНС
- •22.2.4. Оценка точности обсервованного места
- •22.3. Определение места судна с помощью импульсно-фазовых РНС
- •22.3.1. Принцип действия импульсно-фазовой РНС
- •22.3.2. Методы получения обсервованного места судна и оценка его точности
- •Точность определения места
- •22.3.3. Импульсно-фазовая РНС «Лоран-С» (США) и «Чайка» (РФ)
- •Соответствие периода повторения буквенно-цифровому обозначению РНС «Лоран-С»
- •Цепи импульсно-фазовой РНС «Лоран-С» (США) и «Чайка» (РФ)
- •22.3.4. Задачи на определение места судна по гиперболическим РНС
- •Выводы
- •ГЛАВА 23. ГЛОБАЛЬНЫЕ НАВИГАЦИОННЫЕ СПУТНИКОВЫЕ СИСТЕМЫ (ГНСС)
- •23.1. Основные закономерности движения ИСЗ и их орбиты
- •23.1.1. Основные закономерности движения ИСЗ
- •Зависимость периода обращения и скорости ИСЗ от высоты его орбиты
- •23.1.2. Орбиты ИСЗ и их особенности
- •23.2. Особенности навигационного использования ИСЗ (НКА)
- •23.3. Способы радионавигационных определений по НКА
- •23.4. Методы определения места судна по НКА
- •А. Дальномерный метод
- •Б. Псевдодальномерный метод
- •В. Разностно-дальномерный метод (доплеровский интегральный)
- •Г. Радиально-скоростной (доплеровский дифференциальный) метод
- •23.5. Структура глобальных навигационных спутниковых систем
- •А. Общие сведения
- •Б. Подсистема навигационных космических аппаратов
- •В. Подсистема контроля и управления
- •Г. Подсистема навигационной аппаратуры потребителей
- •Д. Информация на дисплее судового приемоиндикатора
- •Е. Сравнительная характеристика ГНСС
- •Сравнительные характеристики GPS (США) и ГЛОНАСС (РФ)
- •Ж. Дифференциальная подсистема ГНСС (ДПС ГНСС)
- •Эксплуатационные требования к морской дифференциальной подсистеме
- •ККС Черного моря (из РТСНО адм. № 3001)
- •З. Точность определения места по среднеорбитальной ГНСС
- •Геометрические факторы в СНС ГЛОНАСС
- •Выводы
- •ГЛАВА 24. ВЕРОЯТНЕЙШЕЕ МЕСТО И РАСЧЕТ БЕЗОПАСНОГО ПУТИ СУДНА
- •24.1. Отыскание вероятнейшего места судна и расчет его точности
- •Какому из этих мест отдать предпочтение и взять за исходное место для дальнейшего счисления пути судна?
- •Задачи на расчет вероятнейшего места судна (для МНК № 3207 или № 32106)
- •24.2. Исключение фигуры погрешностей
- •24.2.1. Общие положения
- •24.2.2. Исключение фигуры погрешностей методом биссектрис
- •24.2.3. Отыскание вероятнейшего места в фигуре погрешностей центрографическим методом
- •24.3. Выбор безопасного пути судна с учетом точности его плавания
- •Коэффициент по заданной вероятности
- •24.4. Расчет периодичности определения места судна для обеспечения заданной точности плавания
- •Задачи на расчет допустимого времени плавания по счислению
- •Периодичность определений места судна (мин.) (допустимое время плавания по счислению)
- •24.5. Рекомендации по анализу счисления пути судна
- •Выводы
- •ГЛАВА 25. СИСТЕМА ОГРАЖДЕНИЯ МАМС И МЕЖДУНАРОДНЫЙ СВОД СИГНАЛОВ
- •25.1. Система ограждения «МАМС»
- •ЛАТЕРАЛЬНЫЕ ЗНАКИ
- •КАРДИНАЛЬНЫЕ ЗНАКИ
- •Условные обозначения характера огня в руководствах для плавання и на картах
- •25.2. Международный свод сигналов (ММС)
- •25.2.1. Общие замечания
- •Значение сигналов предаваемых знаками Морзе флажками (руками):
- •25.2.3. Содержание «МСС-65»
- •Правила пользования сводом (с. 13÷31)
- •Однобуквенные сигналы (с. 35÷41)
- •Общий раздел ММС – 65 (с. 43÷132)
- •Медицинский раздел (с. 133÷167)
- •Приложения (на отдельных вкладных листах)
- •Сигналы о присутствии в районе подводной лодки (в подводном положении)
- •Прием сообщений, касающихся безопасности
- •Указание характера бедствия
- •Сигналы бедствия, предписанные МППСС-72
- •Однобуквенные сигналы, применяемые совместно с цифровыми дополнениями
- •Сигналы, применяемые при всех способах сигнализации
- •Выводы
- •26.1.1. Локсодромия и ее элементы
- •26.1.2. Ортодромия и ее элементы
- •26.2. Основные формулы ортодромии. Способы ее задания
- •26.2.1. Основные формулы ортодромии
- •26.2.2. Способы задания ортодромии
- •26.3. Расчет плавания по локсодромии
- •26.4. Расчет плавания по ортодромии
- •26.4.1. Расчет пройденного по ортодромии расстояния (D)
- •26.4.2. Расчет начального курса плавания по ортодромии (КH)
- •26.4.3. Расчет конечного курса плавания по ортодромии (КK)
- •26.4.4. Расчет значений К0 и λ0
- •26.4.5. Расчет координат промежуточных точек ортодромии
- •26.4.6. Задачи на расчет плавания по ДБК
- •Логарифмы чисел (выдержка из табл. 2 «МТ-75» или табл. 5.44 «МТ-2000»)
- •Меридиональные части (выдержка из табл. 26 «МТ-75» или табл. 2.28а «МТ-2000»)
- •Натуральные значения тригонометрических функций (выдержка из табл. 6-а «МТ-75» или 5.42-а «МТ-2000»)
- •Логарифмы тригонометрических функций (выдержка из табл. 5-а «МТ-75»)
- •Выводы
- •ГЛАВА 27. АНГЛИЙСКИЕ МОРСКИЕ КАРТЫ, РУКОВОДСТВА И ПОСОБИЯ ДЛЯ ПЛАВАНИЯ
- •27.1. Английские морские карты
- •27.1.1. Английские навигационные карты
- •27.1.2. Английские справочные и вспомогательные карты
- •Admiralty Charts and Publications 1608 Approaches Chanakkale bogazi (The Dardanelles)/ Small corrections …. «Depths in meters»
- •27.2. Английские руководства и пособия для плавания
- •Navigational Publications for the professional mariner
- •27.2.1. Английские лоции («Pilots»)
- •«Admiralty List of Lights and For Signals»
- •Содержание каждого тома
- •Выводы
- •ГЛАВА 28. СУДОВАЯ КОЛЛЕКЦИЯ КАРТ, РУКОВОДСТВ И ПОСОБИЙ ДЛЯ ПЛАВАНИЯ
- •28.1. Судовая коллекция карт, руководств и пособий для плавания (СККРиПДП)
- •28.1.1. Комплектование СККРиПДП
- •28.1.2. Хранение, учет, передача и списание карт, руководств и пособий для плавания на судне
- •28.1.3. Каталоги карт и книг
- •28.2. Поддержание карт, руководств и пособий для плавания на уровне современности
- •28.2.1. Общие положения
- •28.2.2. Печатные корректурные документы
- •28.2.3. Навигационные предупреждения, передаваемые по радио
- •28.2.4. Корректурные документы и их хранение на судне
- •28.2.5. Корректура карт, руководств и пособий для плавания на судне
- •Выводы
- •ГЛАВА 29. ПОДГОТОВКА ШТУРМАНСКОЙ ЧАСТИ К РЕЙСУ
- •29.1. Рейсовое задание
- •29.2. Подбор карт, руководств и пособий для плавания на переход
- •А. Карты
- •Б. Руководства и пособия для плавания
- •Классификация руководств и пособий для плавания
- •29.3. Изучение района плавания
- •29.4. Предварительная прокладка пути судна
- •Таблица плавання
- •29.5. Подъем карт и окончательная проработка плана перехода
- •29.5.1. Подъем карт
- •29.5.2. Окончательная проработка плана перехода
- •29.6. Штурманская справка на переход
- •Выводы
- •ГЛАВА 30. ОРГАНИЗАЦИЯ ВАХТЫ НА МОСТИКЕ
- •30.1. Общие принципы организации вахты
- •30.2. Заступление на вахту и ее несение при стоянке судна
- •30.2.1. Обязанности ВПК при стоянке судна в порту
- •30.2.2. Обязанности ВПК при стоянке судна на якоре
- •30.3. Подготовка судна к выходу в море
- •30.4. Прием-сдача ходовой вахты
- •30.5. Наблюдение и вахта на мостике
- •30.6. Определение поправок ТСН
- •30.7. Характерные недостатки технических средств и способов навигации
- •Выводы
- •31.2. Счисление пути судна
- •Условные обозначения для счислимых и обсервованных мест
- •31.3. Определение места судна
- •31.4. Стандарты точности судовождения
- •Международные стандарты точности судовождения
- •Коэффициенты для расчета радиальной погрешности заданной вероятности (для отношения полуосей эллипса погрешностей в/а = 1,0)
- •Международные стандарты точности судовождения
- •Отечественные нормативы точности судовождения
- •31.5. Оценка точности места судна
- •Среднеквадратические погрешности (mU) основных навигационных параметров (из таблицы 4.3. «МТ-2000»)
- •Расчет точности места судна
- •31.6. Маневренные характеристики судна. Лоцманская карточка
- •Лоцманская карточка (из приложения 6 «РШСУ-98»)
- •Характеристика рулевого устройства
- •Проверка наличия на борту и готовности
- •Прочая информация
- •31.7. Правила ведения судового журнала
- •1. Общие положения.
- •2. Порядок заполнения судового журнала.
- •Выводы
- •ГЛАВА 32. НАВИГАЦИОННОЕ ОБЕСПЕЧЕНИЕ ПЛАВАНИЯ В СТЕСНЕННЫХ ВОДАХ
- •32.1. Общая характеристика условий плавания в стесненных водах
- •32.1.1. Основные особенности условий плавания в стесненных водах
- •32.1.2. Безопасная скорость судна
- •Правило 6 «МППСС-72». Безопасная скорость
- •32.2. Подготовка к плаванию в стесненных условиях
- •32.2.1. Навигационные особенности плавания в стесненных условиях
- •Навигационными особенностями плавания в стесненных условиях являются:
- •Специальными мерами, обеспечивающими навигационную безопасность в стесненных водах, являются:
- •32.2.3. Расчет и планирование поворота. Контроль глубин
- •32.2.4. Подготовка к плаванию в стесненных водах
- •Проверочный лист подготовки судна к плаванию в стесненных условиях
- •32.3. Обеспечение навигационной безопасности при плавании в стесненных водах
- •32.3.1. Допустимое расстояние до навигационных опасностей, расположенных по одному борту
- •32.3.2. Допустимое относительное отклонение от оси полосы одностороннего движения
- •32.3.3. Допустимые радиальные СКП места при плавании среди навигационных опасностей
- •32.3.4. Допустимые радиальные СКП места при плавании вблизи навигационных опасностей, расположенных по одному борту
- •32.3.5. Допустимые СКП места по перпендикуляру к оси полосы одностороннего движения
- •32.4. Обязанности судоводителя при плавании в стесненных условиях
- •32.4.1. Обязанности ВПК при плавании судна в стесненных водах
- •32.4.2. Особенности плавания судна по СРД
- •Правило 10 «МППСС-72». Плавание по системам разделения движения
- •32.4.3. Действия ВПК при выходе судна из полосы движения СРД
- •Выводы
- •ГЛАВА 33. НАВИГАЦИОННОЕ ОБЕСПЕЧЕНИЕ ПЛАВАНИЯ СУДНА В ОТКРЫТОМ МОРЕ
- •33.1. Навигационное обеспечение плавания
- •33.1.1. Плавание по наивыгоднейшим путям
- •33.1.2. Оптимальная скорость судна
- •33.1.3. Контроль за местом судна
- •33.2. Судовождение в высоких широтах
- •33.2.1. Навигационные условия плавания
- •33.2.2. Счисление координат судна
- •33.2.3. Особенности определения места судна
- •33.3. Особенности судовождения при плавании в шторм
- •33.3.1. Оценка ветроволновых потерь скорости судна
- •33.3.2. Уклонение от штормовых зон
- •33.3.4. Обязанности судоводителей:
- •Выводы
- •ГЛАВА 34. НАВИГАЦИОННОЕ ОБЕСПЕЧЕНИЕ ПЛАВАНИЯ СУДНА НА МОРЯХ С ПРИЛИВАМИ
- •34.1. Физическая сущность явления приливов и отливов
- •34.2. Основные элементы прилива
- •34.3. Неравенства приливов
- •Суточные (тропические) неравенства
- •Полумесячные (фазовые) неравенства
- •Характеристика прилива по возрасту Луны
- •Параллактические (месячные) неравенства
- •34.4. Таблицы приливов
- •Приливы в основных пунктах (выдержка)
- •Поправки для дополнительных пунктов
- •Поправки высот уровня моря на атмосферное давление
- •34.5. Решение задач с использованием Таблиц приливов
- •Условия индивидуальных задач
- •Задача 2.
- •34.6. График прилива
- •34.7. Предвычисление приливов по гармоническим постоянным
- •34.8. Сведения о приливо-отливных явлениях, помещаемых на картах
- •Негармонические постоянные
- •34.9. Атласы приливо-отливных явлений
- •34.10. Судовождение в морях с приливами
- •Выводы
- •35.1. Подготовка судна к подходу к берегу
- •35.2. Подход судна к берегу с моря
- •35.3. Навигационное обеспечение плавания судна при подходе к побережью
- •35.3.1. Варианты подхода судна к побережью
- •35.3.2. Выбор курсов подхода
- •35.3.3. Опознавание ориентиров
- •35.4. Навигационное обеспечение прибрежного плавания
- •Выводы
- •36.2. Особенности навигационных условий в шхерах
- •36.3. Особенности судовождения в узкостях
- •36.4. Ограждающие и опасные изолинии
- •36.5. Сетки изолиний
- •Выводы
- •37.2. Признаки приближения судна ко льдам, к разводьям и чистой воде
- •37.3 Особенности навигационных условий плавания во льдах
- •37.4 Способы определения скорости хода судна при плавании во льдах
- •37.5. Определение дрейфа судна в сплоченных льдах
- •37.6. Особенности счисления пути судна при плавании во льдах
- •37.7. Действия судоводителей при плавании во льдах
- •Выводы
- •ГЛАВА 38. ОСОБЕННОСТИ СУДОВОЖДЕНИЯ ПО ВВП. ПОСТАНОВКА СУДА НА ЯКОРЬ
- •38.1. Особенности судовождения при плавании по ВВП
- •38.1.1. Основные понятия, определения и термины
- •38.1.2. Особенности навигационных условий ВВП
- •38.1.3. Судоходная обстановка и сигнализация
- •38.1.4. Организация и обеспечение судоходства по ВВП
- •38.1.5. Навигационные пособия
- •38.1.6. Особенности судовождения при плавании по ВВП
- •38.2.Постановка суда на якорь
- •Выводы
- •СИСТЕМА МАМС – РЕГИОН А
- •ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯ, ПРИМЕНЯЕМЫЕ ПРИ ВЕДЕНИИ СУДОВОГО ЖУРНАЛА И РЕШЕНИИ ЗАДАЧ СУДОВОЖДЕНИЯ
- •ПЕРЕЧЕНЬ И ЗНАЧЕНИЕ СОКРАЩЕНИЙ, ИСПОЛЬЗОВАННЫХ В ТЕКСТЕ
- •ПЕРЕЧЕНЬ ЛИТЕРАТУРЫ
ГЛАВА 17. АНАЛИТИЧЕСКОЕ (ПИСЬМЕННОЕ) СЧИСЛЕНИЕ КООРДИНАТ СУДНА
17.1. Сущность и основные формулы аналитического (письменного) счисления
Кроме графического счисления пути судна, учет его плавания может производиться с помощью аналитического (письменного) счисления.
Аналитическое счисление – вычисление географических координат судна по его курсу и плаванию (по сделанным судном разностям широт и долгот) по формулам вручную или с помощью счетно-решающих устройств.
Аналитическое счисление производится по формулам и применяется при плавнии судна вдали от берегов на океанских переходах, когда ведение графического счисления становится неточным из-за больших погрешностей в графических построениях на морских навигационных картах мелкого масштаба.
Чаще всего аналитическое счисление применяется:
1.→ при непрерывной выработке текущих счислимых координат места судна, вводимых в системы судовой автоматики. Задача решается с помощью автоматических счетно-решающих устройств (или ЭВМ);
2.→ при периодическом вычислении счислимых координат места судна в тех случаях, когда необходимо исключить погрешности счисления за счет неточности графических построений,
связанных с прокладкой пути судна на мелкомасштабной карте. Задача решается вручную или с помощью счетно-решающих устройств (для контроля точности графических построений на карте; определения места судна по разновременным наблюдениям светил).
Аналитическое счисление с помощью автоматических счетно-решающих устройств производится по формулам с учетом сжатия Земли. В простейших системах решаются формулы без учета сжатия Земли.
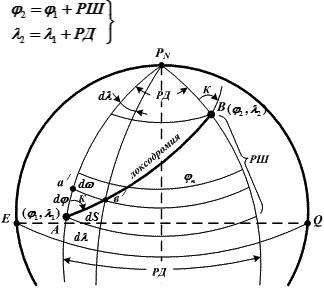
Получим основные формулы аналитического счисления (рис. 17.1).
Судно из точки А (φ1 λ1), следуя постоянным курсом (К) по локсодромии, пришло в точку В (φ2 λ2). Если будут известны сделанные судном разность широт (РШ) и разность долгот (РД) то
координаты точки В (φ2 λ2) легко получить из соотношений:
(17.1)
Рис. 17.1. Аналитическое (письменное) счисление пути судна
Значение разности широт (РШ) и разности долгот (РД) можно рассчитать по известным элементам движения: К → курсу судна и S → плаванию судна по этому курсу.
Считая Землю за сферу (шар) из элементарно малого треугольника Аа′в′: Aa′ = dφ → приращение широты;
b′a′ = dω → приращение отшествия; Ab′ = dS → приращение расстояния,
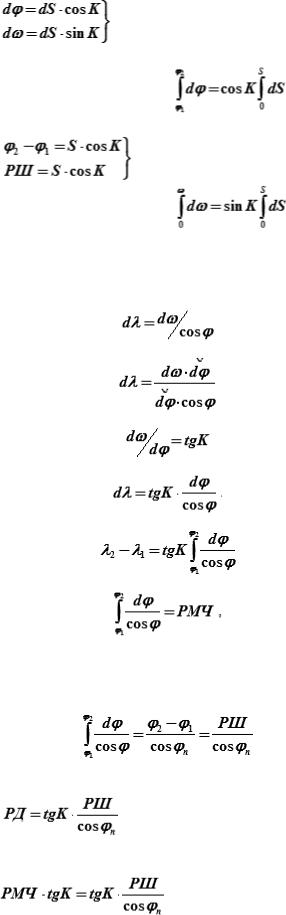
где dφ – разность широт (мили);
dω – расстояние между меридианами по параллели от т. а′ до т. в′ – отшествие (мили);
dS – плавание судна по локсодромии между точкой А и точкой в′ (мили).
Если Аа′в′ принять за плоский, можно написать дифференциальные уравнения:
(17.2)
В результате интегрирования значений dφ и dω при K = const, получим:
1)→
то есть
|
(17.3) |
2)→ |
|
то есть |
|
ω = S · sin K |
(17.4) |
Для вычисления значения разности долгот – РД, воспользуемся соотношением между длиной дуги экватора и параллели:
Умножим числитель (dω) и знаменатель (cos φ) на dφ, тогда
так как из Аа′в′
то
Решение этого уравнения приводит к известному интегралу:
а
тогда |
|
РД = РМЧ · tgK |
(17.5) |
Для вывода прямой связи между отшествием (ОТШ) и разностью долгот (РД), используем теорему о среднем значении интеграла, которая дает:
где φn – промежуточное значение широты в интервале между φ1 и φ2. Тогда для разности долгот – РД можно написать
(17.6)
Приравняв оба значения разности долгот (РД), полученного по формулам (17.5) и (17.6), получим значение промежуточной широты φn:
(17.7)

откуда
(17.8)
Подставив значение соs φn (формула 17.8) в формулу (17.6) для разности долгот (РД) и учтя, что
ОТШ = РШ · tgK, |
(17.9) |
окончательно получим: |
|
|
(17.10) |
где отшествие (ОТШ) и разность широт (РШ) в милях.
Таким образом отшествие (ОТШ) представляет собой длину параллели (в милях) между меридианами точек А и В, широта которой (параллели) определяется соотношением
(17.11)
На практике, при ведении аналитического учета на коротких расстояниях, можно допустить, что в интервале от φ1 до φ2 значение cos φ изменяется линейно, тогда
(17.12)
и приближенная формула для расчета разности долгот – РД примет вид:
(17.13)
то есть разность долгот (РД) равна отшествию (ОТШ), деленному на косинус средней широты (φm).
По формулам (17.3) и (17.4) составлены таблица 24 «МТ-75» (с. 260÷272) и таблица 2.19 а «МТ2000» (с. 282÷294) «Разность широт и отшествие». В этих таблицах по плаванию S (от 0 до 100 миль)
и курсу (через 1°) можно получить готовые значения разности широт (РШ) и отшествия ( ОТШ),
величины которых даны в таблице до сотых долей мили и поэтому могут быть использованы для плаваний (S) в 10 и 100 раз больших (или меньших) → переносом запятой → см. табл. 17.8.
Пример: 1) S = 450 миль, К = 37°, РШ = 359,4 мили к N и ОТШ = 270,8 мили к Е;
2)К = 230°, S = 1860 миль, РШ = 1195,6′ к S и ОТШ = 1424,8′ к W (см. табл. 17.1).
В«МТ-75» помещена также специальная таблица 25а «Разность долгот» (с. 273÷278)
составленная по формуле (17.13).
Аналогичная таблица 2.20 – см. «МТ-2000» (с. 296÷301).
Разность широт и отшествие
(с. 271 «МТ-75» или с. 293 «МТ-2000»)
|
|
|
|
|
|
Таблица 17.1 |
Плавание |
ОТШ |
|
|
РШ |
||
|
|
|
|
|
|
|
100 |
+(1000) |
76,60 |
+ (766,0) |
|
64,28 |
+ (642,8) |
86 |
(860) |
65,88 |
(658,8) |
|
55,28 |
(552,8) |
Σ S = 1860 миль |
Σ ОТШ = 142,48 = (1424,8′) |
|
Σ РШ =119,56 = (1195,6′) |
|||
|
|
|
|
230° |
|
|
Входные аргументы: 1) ОТШ = 1, 2, 3,…9 и 100 миль;
2) φm = 0÷86° через 0,1°.
Получение значений разности долгот (РД) для десятков или сотен миль значений отшествия (ОТШ) делается простым переносом запятой, отделяющей целую часть от дробной в найденных табличных значениях.
Пример Найти значение разности долгот (РД), если φ1 = 60°N, φ2 = 20°N и отшествие – ОТШ = 246′ к
1. W.
Решение:
1.

2. ОТШ = 246′ = 100 + 100 + 40 + 6.
По значениям 100, 100, 40 и 6 для φCP = 40° из табл. 25а «МТ-75» (с. 273) или табл. 2.20 «МТ-2000»
(с. 296) выбираем значения разности долгот (см. табл. 17.2):
Таблица 17.2.
ОТШ |
РД1 |
100′ |
130,5′ |
100′ |
130,5′ |
40′ |
52,2′ |
6′ |
7,8′ |
Σ ОТШ = 246′ |
Σ РД = 321,0′ к W |
Ответ: РД = 321,0′ к W.
Пример По данным примера 1 найти значение разности долгот (РД), используя промежуточную
2.широту (φn).
Решение:
1. → Находим значение φn (см. ф. 17.8).
(17.14)
φ1 = 60°N …. МЧ1 = 4507,4′
φ2 = 20°N…. МЧ2 = 1217,3′
Значения меридиональных частей (МЧ1 и МЧ2) выбираем из табл. 26 «МТ-75» (с. 280÷287) или табл. 2.28а «МТ-2000» (с. 314÷321) → табл. 24.5.
Из табл. 27 «МТ-75» (с. 288) или табл. 2.28б «МТ-2000» (с. 322) «Поправки для получения меридиональных частей шара» выбираем поправки для перехода к меридиональным частям (МЧ1, МЧ2) на шаре (в навигационных задачах Землю принимают за шар).
МЧ1 = +20,0′ (для φ1 = 60°) и МЧ2 = +7,8′ (для φ2 = 20°)
В результате: 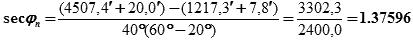
и φn = 43°23′ ≈ 43,4° (см. табл. 6а «МТ-75» (с. 156÷199) или табл. |
5.42 а «МТ-2000» (с. 460) |
«Натуральные значения тригонометрических функций» → табл. 24.6. |
|
2) → Разбиваем значение отшествия – ОТШ = 246′ = 100 + 100 + 40 + 6 и выбираем соответствующие им (100, 100, 40, 6) значения разности долгот – РД из табл. 25а «МТ-75» или 2.20 «МТ-2000», интерполированием между φn = 43° и φn = 43,5° (см. табл. 17.3).
Таблица 17.3.
ОТШ |
РД2 |
100′ |
137,66′ |
100′ |
137,66′ |
40′ |
55,02′ |
6′ |
8,26′ |
Σ ОТШ = 246′ |
Σ РД = 338,6′ к W |
Сравнивая значение разности долгот из табл. 17.2 (РД1 = 321,0′ к W) и значение разности долгот из табл. 17.3 (РД2 = 338,6′ к W) видно (Δ = 17,6′), что при больших значениях разности широт (РШ),
нужно пользоваться не средним значением широты (φСР), а значением промежуточной широты
(φПР).
