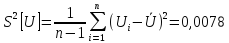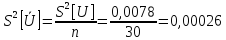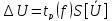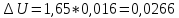5
.docxМИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)
Кафедра Инновационного менеджмента
ОТЧЕТ по лабораторной работе №5 «ОБРАБОТКА РЕЗУЛЬТАТОВ ПРЯМЫХ И КОСВЕННЫХ ИЗМЕРЕНИЙ»
Студентка гр. 5692 ______________ Иванова В.Ю.
Преподаватель ______________ Комаров Б.Г.
Санкт-Петербург
2017 г
Цель работы – ознакомление с методами обработки результатов прямых и косвенных измерений при однократных и многократных измерениях.
Задание
-
Ознакомиться с лабораторным стендом и сменным модулем «Прямые, косвенные и совместные измерения».
-
Прямые однократные измерения. Измерить напряжение на выходе резистивного делителя (по указанию преподавателя). Результат однократного измерения напряжения записать в вид Ux = U ± ΔU.
-
Косвенные однократные измерения. Измерить ток, протекающий через резистивный делитель, путем измерения напряжения на образцовом сопротивлении. Результат однократного измерения тока записать в виде Ix = I ± ΔI.
-
Прямые многократные измерения1. Измерить несколько раз напряжение, указанное в п.2, при наличии относительно больших случайных погрешностей. Обработать полученные данные и результат измерений напряжения записать в виде Ux =
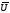 ± ΔU;
± ΔU;
-
Косвенные многократные измерения. Измерить несколько раз ток, определяемый в соответствии с п.3, при наличии относительно больших случайных погрешностей. Обработать полученные данные и результат измерений тока записать в виде Ix =
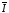 ± ΔI;
± ΔI;
Спецификация применяемых средств измерений
|
Наименование средства измерения |
Пределы измерения Xk |
Класс точности c/d |
|
Вольтметр |
200 мВ, 2 В, |
0.5/0.2 |
|
20 В, 200 В |
1.5/0.2 |
Обработка результатов.
Обработка результатов однократных прямых измерений:
Относительная погрешность при косвенном измерении тока
U0 + R0,
где U0 = – относительная погрешность измерения напряжения, U0 = (U0 / U0) 100% , U0 – абсолютная погрешность измерения напряжения, определяемая по классу точности вольтметра, R0 – относительная погрешность сопротивления образцового резистора (указывается в описании).
U0 + R0=(U0 / U0) 100%+ R0
U0=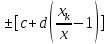 ,
(0.05
,
(0.05
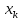 ≤
x
≤
≤
x
≤
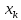 )
)
где
c
= 1.5, d
= 0.2,
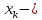 конечное значение диапазона измерений,
x
конечное значение диапазона измерений,
x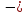 измеренное
значение (результат).
измеренное
значение (результат).
Произведу расчет:
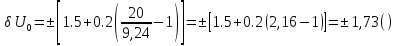
Абсолютная погрешность:
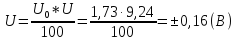
Результат:
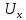 =
=
 =9.24 ± 0.16 (B)
=9.24 ± 0.16 (B)
Обработка результатов однократных косвенных измерений:
Ток, протекающий через резисторы:
I
=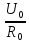 =
=
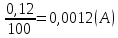
Рассчитаем относительную погрешность измерения тока:
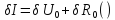
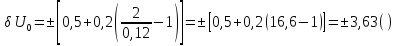
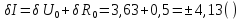
Абсолютная погрешность косвенного измерения тока:
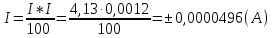
Результат однократного косвенного измерения тока:
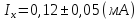
Рассчитаем относительную погрешность измерения напряжения:
Относительная погрешность измерения напряжения
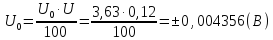
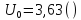
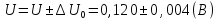
Рассчитаем относительную погрешность измерения мощности:
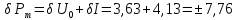 (%)
(%)
 )
)
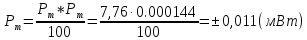
Результат измерения мощности:
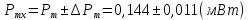
Обработка результатов многократных прямых измерений напряжения:
Таблица
1 P=90%;
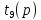 =1,65
=1,65
|
Номер измерения |
Ui, В |
|
ρi ,В |
S2[U] ,В2
|
|
|
1 |
9,03 |
8,73 |
0,30 |
0,0262
|
0,00145
|
|
2 |
8,74 |
0,01 |
|||
|
3 |
8,73 |
0,00 |
|||
|
4 |
8,65 |
-0,08 |
|||
|
5 |
8,9 |
0,17 |
|||
|
6 |
8,89 |
0,16 |
|||
|
7 |
8,79 |
0,06 |
|||
|
8 |
8,5 |
-0,23 |
|||
|
9 |
8,7 |
-0,03 |
|||
|
10 |
8,61 |
-0,12 |
|||
|
11 |
8,73 |
0,00 |
|||
|
12 |
8,38 |
-0,35 |
|||
|
13 |
8,54 |
-0,19 |
|||
|
14 |
8,89 |
0,16 |
|||
|
15 |
8,9 |
0,17 |
|||
|
16 |
8,66 |
-0,07 |
|||
|
17 |
8,79 |
0,06 |
|||
|
18 |
8,76 |
0,03 |
|||
|
|
|
|
|
|
|
-
Найду среднее арифметическое отдельных результатов наблюдений
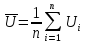
Где
n
– число наблюдений, принять
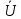 за действительное значение измеряемой
величины(результат измерения)
за действительное значение измеряемой
величины(результат измерения)
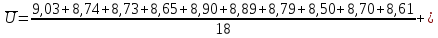
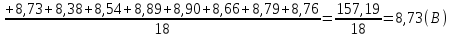
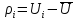
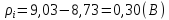
2. Найду оценку дисперсии случайной погрешности измерений
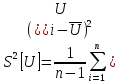
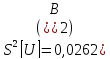
3.Найду оценку дисперсии погрешности результата измерения
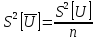
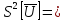 0,00145
0,00145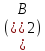
4. Найдем доверительное значение погрешности результата измерения по выражению
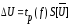 ,
,
где
tp(f)
– коэффициент распределения Стьюдента,
соответствующий задаваемой доверительной
вероятности P
и числу степеней свободы f
. В рассматриваемом случае f
= n
– 1; Значение P=0,9
, значение
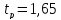
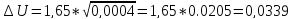
5. Результат измерения напряжения
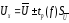
|
Номер измерения |
Ui, В |
|
ρi ,В |
S2[U] ,В2
|
|
|
1 |
8,71 |
8,70 |
0,01 |
0,0078 |
0,00026
|
|
2 |
8,64 |
-0,06 |
|||
|
3 |
9 |
0,30 |
|||
|
4 |
8,57 |
-0,13 |
|||
|
5 |
8,76 |
0,06 |
|||
|
6 |
8,91 |
0,21 |
|||
|
7 |
8,62 |
-0,08 |
|||
|
8 |
8,71 |
0,01 |
|||
|
9 |
8,74 |
0,04 |
|||
|
10 |
8,58 |
-0,12 |
|||
|
11 |
8,78 |
0,08 |
|||
|
12 |
8,67 |
-0,03 |
|||
|
13 |
8,68 |
-0,02 |
|||
|
14 |
8,72 |
0,02 |
|||
|
15 |
8,8 |
0,10 |
|||
|
16 |
8,82 |
0,12 |
|||
|
17 |
8,68 |
-0,02 |
|||
|
18 |
8,81 |
0,11 |
|||
|
19 |
8,68 |
-0,02 |
|||
|
20 |
8,44 |
-0,26 |
|||
|
21 |
8,61 |
-0,09 |
|||
|
22 |
8,53 |
-0,17 |
|||
|
23 |
8,7 |
0,00 |
|||
|
24 |
8,82 |
0,12 |
|||
|
25 |
8,69 |
-0,01 |
|||
|
26 |
8,66 |
-0,04 |
|||
|
27 |
8,74 |
0,04 |
|||
|
28 |
8,93 |
0,23 |
|||
|
29 |
8,56 |
-0,14 |
|||
|
30 |
8,43 |
-0,27 |
|||
|
|
|
|
|
|
|
1.Найдем среднее арифметическое отдельных результатов наблюдений
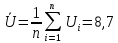
2. Найти оценку дисперсии случайной погрешности измерений
3.Найти оценку дисперсии погрешности результата измерения
4.Доверительный интервал погрешности результата измерений при нормальном законе распределения случайных погрешностей определяется выражением
5. Результат измерения напряжения
Вывод: в лабораторной работе были произведены прямые и косвенные измерения. Было выяснено, что при увеличении количества измерений уменьшается случайная составляющая погрешности измерений; напряжение, измеренное без помех, соответствует среднему значению напряжения, измеренного с помехами с учётом погрешности.
1 Примечание 2. Для иллюстрации достоинств многократных измерений эксперименты п.п. 4 и 5 по указанию преподавателя могут быть проведены дважды: при небольшом числе измерений (5 – 7) и числе измерений 20 – 25. Число измерений и количество экспериментов задаются преподавателем.

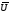 ,
В
,
В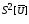 ,В2
,В2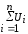 =157,19
=157,19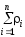 =0
=0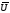 ,
В
,
В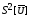 В2
В2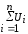 =260,99
=260,99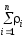 =0
=0