Лабораторная работа №55

Лабораторная работа №5

Упражнение 1

Найти приближенное решение уравнения , удовлетворяющего начальному условию , на отрезке () методом ломаных Эйлера с заданной точностью .

Порядок выполнения упражнения:

1. Для отыскания приближенного решения создайте М-функцию.

В качестве входных аргументов функции используйте: заданную в символьном виде функцию ; ее символьные аргументы , ; координаты начальной точки ,; координаты и концов отрезка, на котором ищется решение; начальное число отрезков разбиения , точность .

В качестве выходных аргументов функции используйте: массивы координат вершин ломаной Эйлера и число отрезков разбиения , понадобившихся для построения приближенного решения с заданной точностью.

Код M-функции должен включать:

а) Последовательное вычисление координат вершин ломаной Эйлера для числа отрезков разбиения , , и т.д. до тех пор, пока не будет достигнута точность (правило, по которому оценивается точность, изложено перед упр. 1).

б) Построение в графическом окне figure 1 в одной системе координат трех ломаных Эйлера с числом звеньев, равны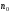м , и (полученных в результате первой, второй и последней итерации); ломаные должны быть изображены разными цветами.

2. Для тестирования М-функции из п.1 используйте решение уравнения с начальным условием на отрезке с точностью . Вначале найдите «вручную» точное решение. Тестирование оформите в виде scriptа.

Код scriptа должен включать:

а) Задание входных аргументов М-функции из п.1, вызов М-функции, отыскание приближенного решения с заданной точностью.

б) Оценку реальной точности приближения: вычисление максимального отклонения в узлах сетки найденного приближенного решения от полученного аналитически точного решения.

в) Построение в графическом окне figure 2 в одной системе координат двух графиков: приближенного и точного решения.

function [x2, y2, n0] = Eler(f, x, y, x0, y0, a, b, n0, eps)

n = n0 / 2;

maxdy = 2 * eps;

Y = 0;

step = 0;

hold on; grid on;

while (maxdy > eps)

n = n * 2;

lastY = Y;

step = step + 1;

dx = (b - a) / n;

X(1) = x0;

Y(1) = y0;

for i = (2 : n + 1)

X(i) = X(i - 1) + dx;

Y(i) = Y(i - 1) + subs(subs(f, x, X(i - 1)), y, Y(i - 1)) * dx;

end

if (step ~= 1)

dy = abs(Y(1) - lastY(1));

maxdy = dy;

for i = (2 : n / 2 + 1)

dy = abs(Y(i * 2 - 1) - lastY(i));

if (dy > maxdy)

maxdy = dy;

end

end

end

if (step == 1)

for i = (1 : n)

plot(X, Y, 'r');

end

end

if (step == 2)

for i = (1 : n)

plot(X, Y, 'b');

end

end

end

plot(X, Y, 'g');

end

>> syms x y;

>> [X, Y, n] = Eler (x * y, x, y, 0, 1, 0, 1, 3, 0.001);

>> y = exp(x^2 / 2);

>> n

n = 1536

>> abs(Y(n + 1) - subs(y, x, X(n + 1)))

ans = 0.000715222

>> figure;

>> hold on;

>> grid on;

>> plot(X, Y, 'g', 'LineWidth', 4);

>> ezplot(y, [0, 1]);

Упражнение 2.

Найти приближенное решение уравнения , удовлетворяющего начальному условию , методом последовательных приближений Пикара.

Порядок выполнения упражнения:

1. Для отыскания приближенного решения создайте М-функцию.

В качестве входных аргументов функции используйте: заданную в символьном виде функцию ; ее символьные аргументы , ; координаты начальной точки ,; число итераций .

В качестве выходных аргументов функции используйте: массив приближенных решений, соответствующих 1-ой, 2-ой, …, -ой итерации.

Код M-функции должен включать:

а) Последовательное отыскание приближенных решений с 1-ой по -ю итерацию.

б) Построение в одной системе координат графиков приближенных решений, соответствующих 1-ой, 2-ой, …, -ой итерации.

2. Для тестирования М-функции из п.1 используйте решение уравнения с начальным условием на отрезке . Вначале найдите «вручную» точное решение. Тестирование оформите в виде scriptа.

Код scriptа должен включать:

а) Задание входных аргументов М-функции из п.1; вызов М-функции, последовательное отыскание приближенный решений, соответствующих 1-ой, 2-ой, …, -ой итерации.

б) Оценку реальной точности приближения: вычисление на отрезке максимального отклонения приближенного решения, соответствующего итерации , и точного решения.

в) Построение в той же системе координат, где были построены приближенные решения, графика точного решения.

function [fx] = Picar(f,x0,y0,n)

clf; grid on; hold on;

syms t; syms x; syms fx;

fx(1)=y0;

h=subs(f,{'x','y'},[t, fx(1)]);

r = fx(1) + int(h,t,x0,x);

fx(2) = sym(r);

for i=2:n

h=subs(f,{'x','y'},[t, fx(i)]);

r = fx(i) + int(h,t,x0,x);

fx(i+1) = sym(r);

end;

line([-10 10], [0 0], 'lineWidth', 1, 'Color', 'black');

line([0 0], [-10 10], 'lineWidth', 1, 'Color', 'black');

axis([-10 10 -1 19]);

for i=1:1:n

x = -10:0.1:10;

y = subs(fx(i), 'x', x);

plot(x,y);

pause(0.25);

end;

plot(x,y,'r', 'lineWidth', 2);

end

-7-