Лабораторная работа №7

Лабораторная работа №7

Упражнение 1.

а) Вычислите частные производные первого и второго порядка функции .

б) Найдите градиент функции в точке .

clear all; clc;

syms x y;

z = cos(3*x+y^2);

disp(['z = ', char(z)]);

dz_dx = diff(z, x);

disp(['dz/dx = ', char(dz_dx)]);

dz_dy = diff(z, y);

disp(['dz/dy = ', char(dz_dy)]);

d2z_dxdx = diff(dz_dx, x);

disp(['d2z/dx^2 = ', char(d2z_dxdx)]);

d2z_dydy = diff(dz_dy, y);

disp(['d2z/dy^2 = ', char(d2z_dydy)]);

d2z_dxdy = diff(dz_dx, y);

disp(['d2z/dxdy = ', char(d2z_dxdy)]);

z = cos(y^2 + 3*x)

dz/dx = -3*sin(y^2 + 3*x)

dz/dy = -2*y*sin(y^2 + 3*x)

d2z/dx^2 = -9*cos(y^2 + 3*x)

d2z/dy^2 = - 2*sin(y^2 + 3*x) - 4*y^2*cos(y^2 + 3*x)

d2z/dxdy = -6*y*cos(y^2 + 3*x)

clear all; clc;

syms x y z;

f = 2*x^3*y+z-x

x0 = 1; y0 = 2; z0 = -3;

f_0 = [x0,y0,z0]

grad=[subs(subs(diff(f,x),x,x0),y,y0),subs(diff(f,y),x,x0),diff(f,z)]

f = 2*y*x^3 - x + z

f_0 = 1 2 -3

grad = [ 11, 2, 1]

Упражнение 2.

Вычислите якобиан перехода от декартовой системы координат к цилиндрической (переход осуществляется по формулам: , , ).

>> syms r phi x y z;

>> x = r * cos(phi);

>> y = r * sin(phi);

>> A = [diff([x; y; z], r), diff([x; y; z], phi), diff([x; y; z], z)];

>> I = det(A)

I = r*cos(phi)^2 + r*sin(phi)^2

>> simple(I)

ans = r

Упражнение 3.

а) Найдите первый дифференциал функции в точке , если , .

б) Создайте М-функцию, вычисляющую первый дифференциал функции в точке при приращениях , . В число входных параметров включите функцию , ее аргументы и их приращения , , заданные в символьном виде, координаты точки и числовые значения приращений аргументов. В число выходных параметров включите символьное выражение первого дифференциала в точке и его числовое значение при заданных приращениях аргументов. Протестируйте М-функцию, используя данные пункта а).

function [df, DF] = u_3(f, x, y, dx, dy, x0, y0, dx0, dy0)

df = diff(f, x) * dx + diff(f, y) * dy;

DF = subs(df, [x,y,dx,dy], [x0,y0,dx0,dy0]);

end

>> syms x y dx dy;

>> z = x * y^2 + 2 * y - x^2;

>> dz = diff(z, x) * dx + diff(z, y) * dy;

>> subs(dz, [x,y,dx,dy], [2,-1,0.1,-0.2])

ans = 0.1000

[A, B] = u_3(z, x, y, dx, dy, 2, -1, 0.1, -0.2)

A = dy*(2*x*y + 2) - dx*(2*x - y^2)

B = 0.1000

Упражнение 4.

а) Найдите второй дифференциал функции в точке , если , .

б) Создайте М-функцию, вычисляющую второй дифференциал функции в точке при приращениях , . В число входных параметров включите функцию , ее аргументы и их приращения , , заданные в символьном виде, координаты точки и числовые значения приращений аргументов. В число выходных параметров включите символьное выражение второго дифференциала в точке и его числовое значение при указанных приращениях аргументов. Протестируйте М-функцию, используя данные пункта а).

function [d2f, D2F] = u_4(f, x, y, dx, dy, x0, y0, dx0, dy0)

d2f = diff(f,x,2)*dx^2+2*diff(diff(f,x),y)*dx*dy+diff(f,y,2)*dy^2;

D2F = subs(d2f, [x,y,dx,dy], [x0,y0,dx0,dy0]);

end

>> syms x y dx dy;

>> z = x * y^2 + 2 * y - x^2;

>> [A, B] = u_4(z, x, y, dx, dy, 2, -1, 0.1, -0.2)

A = -2*dx^2 + 4*y*dx*dy + 2*x*dy^2

B = 0.2200

Упражнение 5.

а) Создайте М-функцию, раскладывающую функцию в точке в ряд Тейлора до членов 1-го порядка включительно. В число входных параметров включите функцию , ее аргументы и их приращения , , заданные в символьном виде, координаты точки и числовые значения приращений аргументов. В число выходных параметров включите символьное разложение функции по формуле Тейлора в точке до членов 1-го порядка включительно, записанное через произвольные значения аргументов функции, а также приближенное значение функции в точке , (значение ) при указанных значениях .

б) Используйте М-функцию из п. а) для вычисления приближенного значения функции в точке . Сравните полученный результат с точным значением этой функции в указанной точке.

в) Постройте в одной системе координат в области , поверхности и .

Замечание. Уравнение , или в развернутом виде

,

является уравнением касательной плоскости к поверхности в точке с координатами .

>> syms x y dx dy;

>> z = (2 * x^2 + y^2)^2;

>> [A, B] = u_4(z, x, y, dx, dy, 0.8, 2.2, 0.001, 0.001)

A = (48*x^2 + 8*y^2)*dx^2 + (8*x^2 + 12*y^2)*dy^2 + 32*x*y

B = 56.3201

>> subs(z, [x, y], [0.8, 2.2])

ans = 37.4544

>> [X, Y] = meshgrid((-6 : 0.2 : 6), (-6 : 0.2 : 6));

>> Z = (2.*X.^2+Y.^2).^2;

>> mesh(X, Y, Z);

Упражнение 6.

а) Создайте М-функцию, раскладывающую функцию в точке по формуле Тейлора до членов 2-го прядка включительно. В число входных параметров включите функцию , ее аргументы и их приращения , , заданные в символьном виде, координаты точки и числовые значения приращений аргументов. В число выходных параметров включите символьное разложение функции по формуле Тейлора в точке до членов 2-го порядка включительно, записанное через произвольные значения аргументов функции, а также приближенное значение функции в точке , (значение ) при указанных значениях .

б) Используйте М-функцию из п. а) для вычисления приближенного значения функции в точке . Сравните полученный результат с точным значением этой функции в указанной точке и с ее приближенным значением, полученным по формуле Тейлора до членов 1-го порядка.

в) Постройте в одной системе координат в области , поверхности , и .

>> syms x y dx dy;

>> z = (2 * x^2 + y^2)^2;

>> [A, B] = u_4(z, x, y, dx, dy, 0.8, 2.2, 0.001, 0.001)

A = (48*x^2 + 8*y^2)*dx^2 + (8*x^2 + 12*y^2)*dy^2 + 32*x*y

B = 56.3201

>> subs(z, [x, y], [0.8, 2.2])

ans = 37.4544

>> hold on;

>> [X, Y] = meshgrid((-6 : 0.2 : 6), (-6 : 0.2 : 6));

>> Z = (2 .* X.^2 + Y.^2).^2;

>> mesh(X, Y, Z);

>> Z = subs(z, [x, y], [0.8, 2.2]) + subs(diff(z, x), [x, y], [0.8, 2.2]).*(X-0.8) + subs(diff(z, y), [x, y], [0.8, 2.2]).*(Y-2.2);

>> Z = double(Z);

>> mesh(X, Y, Z);

>> Z = subs(A, [x, y, dx, dy], {0.8, 2.2, X - 0.8, Y - 2.2});

>> Z = double(Z);

>> mesh(X, Y, Z);

Упражнение 1С

Вычислите якобиан перехода от декартовой системы координат к сферической (переход осуществляется по формулам: , , ).

>> syms x y z r phi theta;

>> x = r * cos(phi) * cos(theta);

>> y = r * sin(phi) * cos(theta);

>> z = r * sin(theta);

>> A = [diff([x; y; z], r), diff([x; y; z], phi), diff([x; y; z], theta)];

>> I = det(A)

I = r^2*cos(phi)^2*cos(theta)^3 + r^2*cos(phi)^2*cos(theta)*sin(theta)^2 + r^2*cos(theta)^3*sin(phi)^2 + r^2*cos(theta)*sin(phi)^2*sin(theta)^2

>> simple(I)

ans = r^2*cos(theta)

Упражнение 2С

Создайте М-функцию, раскладывающую функцию в точке по формуле Тейлора до членов 2-го порядка включительно ( - произвольное число). В число входных параметров включите саму функцию , заданную в символьном виде, координаты точки , приращения ,…,. В число выходных параметров включите символьное разложение функции по формуле Тейлора до членов 2-го порядка включительно, записанное через приращения ,…, независимых переменных, а также приближенное значение функции в указанной точке , …, 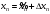(значение ).

Протестируйте М-функцию на примерах.

>> syms x y z dx dy dz;

>> f = x^2 + y^3 + z^4;

>> [A, B] = u_C2(f, [x, y, z], [dx, dy, dz], [1, 2, 3], [0.01, 0.02, 0.03])

A = dx^2 + 2*dx + 6*dy^2 + 12*dy + 54*dz^2 + 108*dz + 90

B = 93.5511

function [A, B] = u_C2(f, X, dX, X0, dX0)

t = length(X);

df = 0;

for i = (1 : t)

df = df + diff(f, X(i)) * dX(i);

end

d2f = 0;

for i = (1 : t)

for j = (1 : t)

d2f = d2f + diff(diff(f, X(i)), X(j)) * dX(i) * dX(j);

end

end

A = f + df + d2f / 2;

A = subs(A, X, X0);

B = subs(A, dX, dX0);

end

-9-