6 Молекулярная физика и термодинамика

Тест 6 – 1

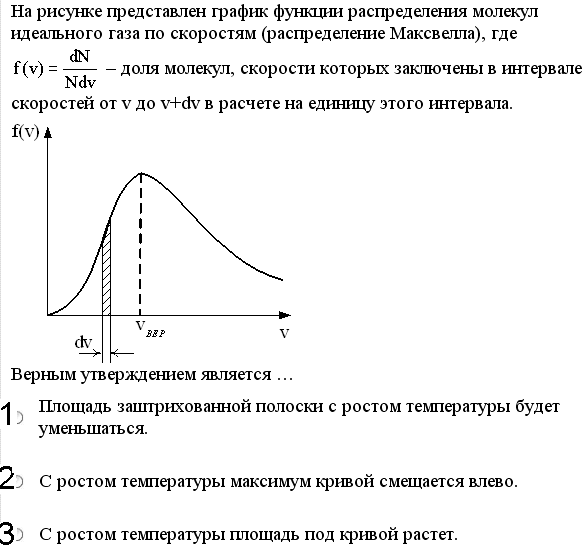
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), гдеf (v) = dN / (N·dv) - доля молекул, скорости которых заключены в интервале скоростей от v до (v+dv) в расчете на единицу этого интервала. Верным утверждением является ...

Варианты ответов: 1) Площадь заштрихованной полоски с ростом температуры будет уменьшаться. 2) С ростом температуры максимум кривой смещается влево.

3) С ростом температуры площадь под кривой растет.

Решение.

Начнём с анализа третьего утверждения. Площадь, ограниченная графиком функции распределения f(v) и осью абсцисс, численно равна единице, так как функция распределения удовлетворяет условию нормировки. Следовательно, с изменением температуры площадь остается постоянной, поэтому третье утверждение является неверным.

Проанализируем второе утверждение. Максимум функции распределения приходится на значение скорости, называемой наиболее вероятной, которая равна: v _вер = , где k - постоянная Больцмана, Т – абсолютная температура, - масса молекулы. Из этой формулы следует, что с ростом температуры максимум кривой смещается вправо, а не влево. Поэтому второе утверждение также неверно.

Рассмотрим первое утверждение. Площадь заштрихованной полоски приблизительно равна площади параллелограмма, которая равна произведению основания на высоту, т.е. f(v)·dv. Но значение f(v) уменьшается с ростом температуры, так как эта функция удовлетворяет условию нормировки, а значение dv остаётся неизменным, поэтому их произведение уменьшается, и площадь заштрихованной полоски с ростом температуры будет уменьшаться. Следовательно, утверждение 1 является верным.

Ответ: вариант 1.

Тест 6 – 2

На рисунке теста 6 – 1 представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где f (v) =dN / (N·dv) - доля молекул, скорости которых заключены в интервале скоростей от v до (v+dv) в расчете на единицу этого интервала.

Если, не меняя температуры и числа молекул, взять другой газ с большей молярной массой, то...

Варианты ответов:

1) площадь под кривой увеличится; 2) максимум кривой сместится вправо в сторону больших скоростей; 3) максимум кривой сместится влево в сторону меньших скоростей.

Решение.

Начнём с анализа первого утверждения. Площадь, ограниченная графиком функции распределения f(v) и осью абсцисс, численно равна единице, так как функция распределения удовлетворяет условию нормировки. Следовательно, с изменением массы молекулы площадь остается постоянной, поэтому первое утверждение является неверным.

Рассмотрим два других утверждения. Максимум функции распределения приходится на значение скорости, называемой наиболее вероятной. Наиболее вероятная скорость равна: v _вер = , где - постоянная Больцмана, Т – абсолютная (или термодинамическая) температура, - масса молекулы. Эту формулу можно записать в другом виде: v _вер =, где R – газовая постоянная, μ – молярная масса. Из этой формулы следует, что с ростом молярной массы максимум кривой смещается влево, а не вправо. Поэтому второе утверждение также неверно. Следовательно, верным является третье утверждение.

Ответ: вариант 3.