4 Колебания и волны

Тест 4 – 1

Материальная точка совершает гармонические колебания с амплитудой А =4 см и периодом Т=2 с. Если смещение точки в момент времени, принятый за начальный, равно нулю, то точка колеблется (в соответствии с уравнением СИ)...

Варианты ответов:

1. х = 0,04∙sin (2t) ; 2) х = 0,04∙cos (2t);

3. x = 0,04∙sin(π t); 4) x = 0,04∙cos (π t).

Решение.

Уравнение гармонических колебаний имеет вид: x = A∙sin (ω ₀ t + α) или x = A∙ cos (ω ₀ t + α), где A – амплитуда, α – начальная фаза, ω ₀ – частота собственных колебаний, которая связана с периодом: ω ₀ = 2π/Т. По условию задачи: А = 0.04 м, α = 0, ω ₀ = 2π/2 = π , x(0)=0. Начальному условию удовлетворяет формула 3.

Ответ: вариант 3.

Тест 4 – 2

Складываются два гармонических колебания одного направления с одинаковыми периодами и равными амплитудами А₀. При разности

фаз ∆φ = 3π/2 амплитуда результирующего колебания равна...

Варианты ответов:

1) 5 А₀ /2; 2) А₀; 3) 2 А₀; 4) 0.

Решение.

Для того чтобы сложить два колебания одинаковой частоты (или периода) и одинакового направления, нужно воспользоваться методом векторных диаграмм. Нужно представить каждое колебание в виде вектора, длина которого равна амплитуде, а угол наклона к оси абсцисс равен начальной фазе. Тогда для нахождения результирующей амплитуды нужно применить теорему косинусов:

А² = А₁² + А₂² + 2∙А₁∙А₂∙cos ∆φ, где ∆φ - разность фаз . На рисунке показана векторная диаграмма, соответствующая условию теста 4 – 2. В нашем примере векторы А ₁и А ₂ имеют одинаковую длину, т.к. их амплитуды одинаковы: А ₁= А ₂=А₀ , а угол между векторами А ₁ и А ₂ равен разности фаз: ∆φ = 3π/2 = - π/2. Применим теорему косинусов для нахождения результирующей амплитуды: А² = А₀² + А₀² + 2∙А₀∙А₀∙cos(-π/2). Так как cos(-π/2)=0, то А² = А₀² + А₀² и результирующая амплитуда, найденная по теореме Пифагора, будет равна: А = А ₀ . Ответ: вариант 2.

Тест 4 – 3

Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет максимальную амплитуду при разности фаз, равной … Варианты ответов: 1) 0; 2) π; 3) π /4 ; 4) π /2 .

Решение.

При сложении гармонических колебаний одинакового направления нужно воспользоваться методом векторных диаграмм, а именно, каждое колебание представить в виде вектора. Если эти вектора имеют одинаковое направление, т.е. разность фаз равна нулю, то их амплитуды складываются и результирующая амплитуда будет максимальной.

Ответ: вариант 1.

.

Тест 4 – 4

Уравнение движения пружинного маятника

d²x/dt² + (b/m)∙dx/dt + (k/m)·x = 0

является дифференциальным уравнением ...

Варианты ответов: 1) вынужденных колебаний;

2) свободных затухающих колебаний;

3) свободных незатухающих колебаний.

Решение.

Проанализируем варианты ответов.

Дифференциальное уравнение вынужденных колебаний имеет вид:

d²x/dt² + 2β·(dx/dt) +ω₀²x = F/m,

где β – коэффициент затухания, ω₀ – частота собственных колебаний. Это уравнение является неоднородным, т.е. правая часть уравнения не равна нулю и содержит слагаемое, связанное с вынуждающей силой.

Так как в заданном уравнении правая часть равна нулю, то рассматриваемое уравнение является однородным. Следовательно, оно представляет собой уравнение свободных колебаний. В дифференциальном уравнении свободных затухающих колебаний должно присутствовать слагаемое, содержащее первую производную от смещения по времени, связанное с наличием силы трения. Такое слагаемое есть в этом уравнении. Поэтому, рассматриваемое уравнение является дифференциальным уравнением свободных затухающих колебаний. Ответ: вариант 2.

Тест 4 – 5

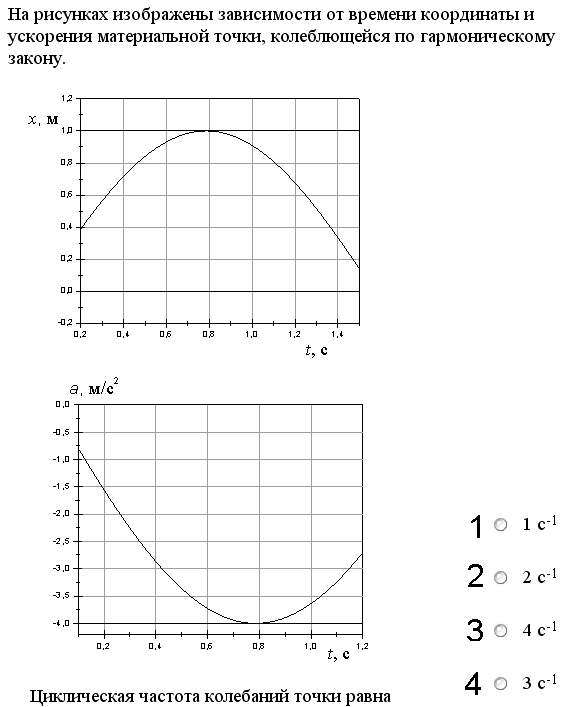На рисунках изображены зависимости от времени координаты и ускорения материальной точки, колеблющейся по гармоническому закону.

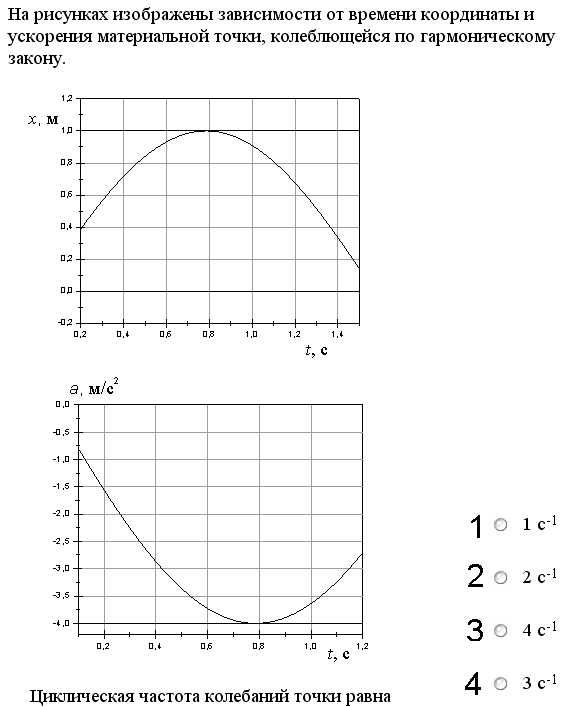Циклическая частота ω₀ колебаний точки равна:

Варианты ответов: 1) 1с^-1; 2) 2с^-1; 3) 4с^-1; 4) 3с^-1.

Решение.

Пусть уравнение гармонических колебаний имеет вид: x = A cos (ω ₀t + α ₀). Тогда найдем ускорение как вторую производную от смещения по времени:

а = - A ω ₀ ² cos (ω ₀t + α ₀). Из сопоставления этих формул, получим: а = - ω ₀ ² ·х. Из графиков для одного и того же момента времени t найдём х и а. Например, для t = 0.8 с х = 1 м, а = - 4 .0 м/с ². Подставим эти числа в последнюю формулу и найдём ω ₀ ² = 4. Отсюда ω ₀=2 с -¹. Ответ: вариант 2.

Тест 4 – 6

На рисунке изображен график затухающих колебаний, где S -колеблющаяся величина, описываемая уравнением:

S(t) = A_o e^-t/τ sin(ω₁t+ φ). Определите время релаксации τ (в с).

Варианты ответов:

1) 3; 2) 1; 3) 2; 4) 0,5.

Решение.

Временем релаксации называется время, в течение которого амплитуда уменьшается в е раз. Число е равно: е = 2.7…. Из рисунка видно, что в момент времени t ₁ = 0 амплитуда равна А₁ = 2.7,а в момент времени t₂ = 2 с амплитуда А₂ = 1. Следовательно, время релаксации τ = t₂ - t ₁ = 2-0 =2 с, т.к. за это время амплитуда уменьшилась А₁/ А₂ = 2.7 = е раз.

Ответ: вариант 3.

Тест 4 – 7

Уменьшение амплитуды колебаний в системе с затуханием характеризуется временем релаксации. Если при неизменном коэффициенте трения среды увеличить в 2 раза массу грузика на пружине, то время релаксации…

Варианты ответов: 1) увеличится в 2 раза; 2) уменьшится в 4 раза;