Файловый архив студентов. Файловый архив студентов.
1296 вузов, 5031 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Государственный университет морского и речного флота им. С.О. Макарова
Предмет:
Гидротехнические сооружения
Файл:
Gidravlika_prezentatsii / 4. Расчет трубопроводов.pptx
Скачиваний:
92
Добавлен:
01.10.2017
Размер:
226.09 Кб
Скачать
☆
►Содержание►

Гидравлическ ий расчет трубопроводо

в

Длинные и короткие трубопроводы

Гидравлически длинными называются такие трубопроводы, у которых в общей сумме потерь энергии преобладают потери на трение, распределенные по длине, а доля местных потерь настолько мала, что ею можно пренебречь при гидравлических расчетах.

К гидравлически коротким относят трубопроводы, в которых сумма местных потерь сравнима с величиной потерь на трение и при расчетах необходимо учитывать и потери напора на трение, и потери напора на местных сопротивлениях.

Три основных типа задач:

1)заданы диаметр d, длина трубопровода l и расход движущейся жидкости Q – требуется определить напор H, необходимый для пропуска заданного расхода.

2)заданы диаметр d и длина трубопровода l, а также действующий напор H – требуется определить расход Q.

3)заданы длина трубопровода l, расход Q и действующий напор H – требуется определить необходимый диаметр трубопровода d.

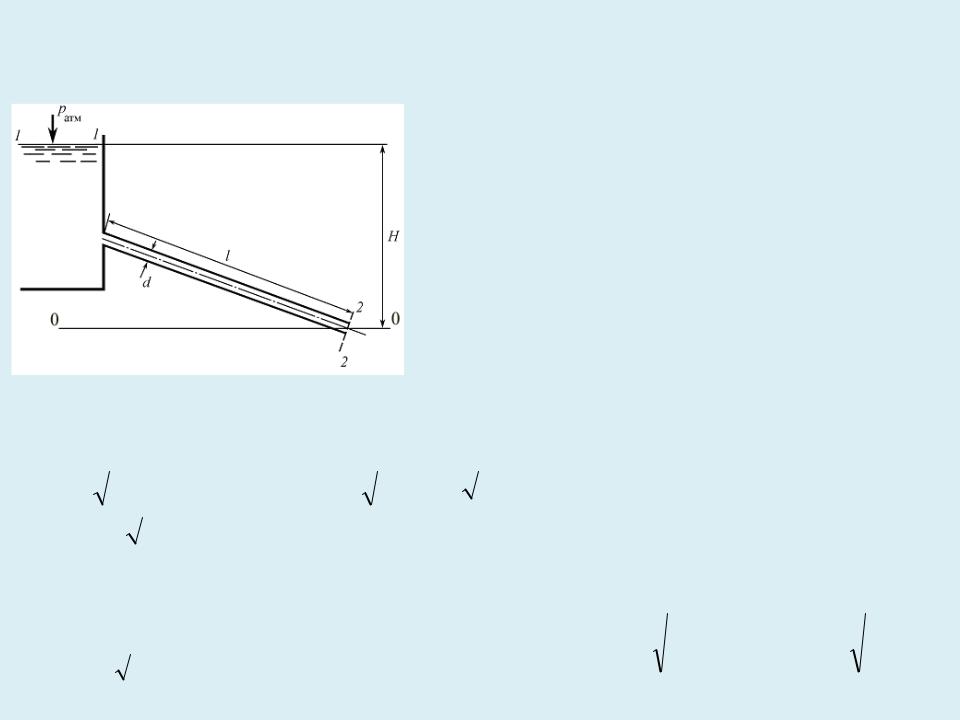
Расчет простых трубопроводов

 

 

p1

 

2

 

 

 

 

 

 

p2

 

2

 

 

z

 

1 1

 

 

 

z

 

 

 

2 2

 

 

 

 

H

 

 

 

 

2

 

 

.

 

1

g

 

2 g

 

 

 

g

 

2 g

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 0,

 

p1 p2

 

pатм ,

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 2

0,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 g

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z1 H;

 

z2 0,

 

 

 

 

 

H z1 z2.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

p

 

2

 

 

 

 

 

p

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z

 

1

 

 

1 1 z

2

 

 

 

2

 

2

 

2 h .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

g

 

2 g

 

 

g

2 g

 

пот

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

H hпот .

 

 

 

 

 

hпот

l 2

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

d 2 g

Пусть заданы длина l, диаметр d и расход Q.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C

 

 

,

 

 

 

 

Q C

 

K

 

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ri

 

 

 

 

Ri

i

 

 

 

 

 

 

 

 

 

 

Q2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

– модуль расхода трубы.

 

 

 

 

 

 

 

 

H

 

l.

 

 

 

 

 

 

 

K C R

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

K 2

 

 

 

 

 

 

 

 

 

Q2

 

 

 

 

 

 

 

 

Q2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

h

 

 

,

 

h

 

 

 

 

l.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

пот

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

l

 

 

K 2

 

 

пот

 

 

 

K 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

1

 

 

 

 

 

 

 

8

 

 

 

Q K

 

 

H .

 

 

 

K Q

 

 

l

.

 

 

 

 

 

 

 

 

 

2

1 d

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

d

6 d

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

d 3.

 

 

 

 

 

 

l

 

 

 

 

 

 

 

 

 

 

H

K C R

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

4

 

 

 

10,08 n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Расчет простых трубопроводов

Порядок расчетов для задач первого типа (заданы диаметр d, длина трубопровода l и расход движущейся жидкости Q – требуется определить напор H):

1. По известному диаметру трубы рассчитываются площадь поперечного

сечения и средняя скорость течения Q .

 

d

 

2. Вычисляется число Рейнольдса

Re

 

.

 

 

 

 

3.В соответствии с материалом и состоянием (новый или бывший в эксплуатации) трубопровода по гидравлическим таблицам определяется его шероховатость.

4.По рассчитанным числу Re и шероховатости из графиков Никурадзе определяется, какой случай сопротивления по длине имеет место. Это позволит выбрать вид формулы для расчета коэффициента C.

5.Рассчитывается или из гидравлических таблиц определяется значение

модуля расхода K.

H Q

2

6. При известных Q, l и K находится величина напора:

2 l.

 

K

 

Расчет простых трубопроводов

В задачах второго типа (заданы диаметр d, длина трубопровода l и напор H – требуется определить расход Q) изначально нельзя вычислить скорости, рассчитать число Рейнольдса и определить закон сопротивления по длине трубы.

В задачах третьего типа (заданы длина трубопровода l, расход Q и напор H – требуется определить диаметр трубопровода d) неизвестны также изначальные характеристики шероховатости трубопровода.

Такие задачи решаются путем последовательных приближений, при котором предварительные расчеты проводят, задаваясь некоторыми начальными значениями неизвестных параметров. После получения результата производится коррекция начальных предположений, и расчеты повторяются. При использовании возможностей современной вычислительной техники эти методы не вызывают принципиальных трудностей.

Если же рассматриваются трубопроводы с заведомо большой скоростью течения и значительной шероховатостью, то это позволяет уверенно предположить наличие квадратичного закона сопротивления. Тогда, применяя формулы Шези, Павловского или Маннинга, можно решать такие задачи без подбора.

Последовательное соединение трубопроводов

Для нахождения потерь по длине или расчетного напора необходимо вычислить по отдельности потери энергии на каждом участке и сложить их:

i n

H hпот i hпот 1 hпот 2 ... hпот n. i 1

 

 

i n

li

 

 

l1

 

l2

 

ln

 

 

2

 

2

 

...

 

 

 

 

H Q

 

2

Q

2

 

2

2

 

 

.

 

 

i 1 Ki

 

 

K1

 

K2

 

Kn

 

HQ2 l.

K 2

Q

 

H

 

 

 

.

i n

l

 

 

 

i

 

 

 

 

 

 

 

2

 

 

 

 

 

i 1

Ki

 

 

 

l

– модуль или удельное сопротивление трубы.

 

 

 

 

 

 

 

K 2

i n

li

 

 

 

 

– суммарный модуль сопротивления всего трубопровода.

2

i 1 Ki

 

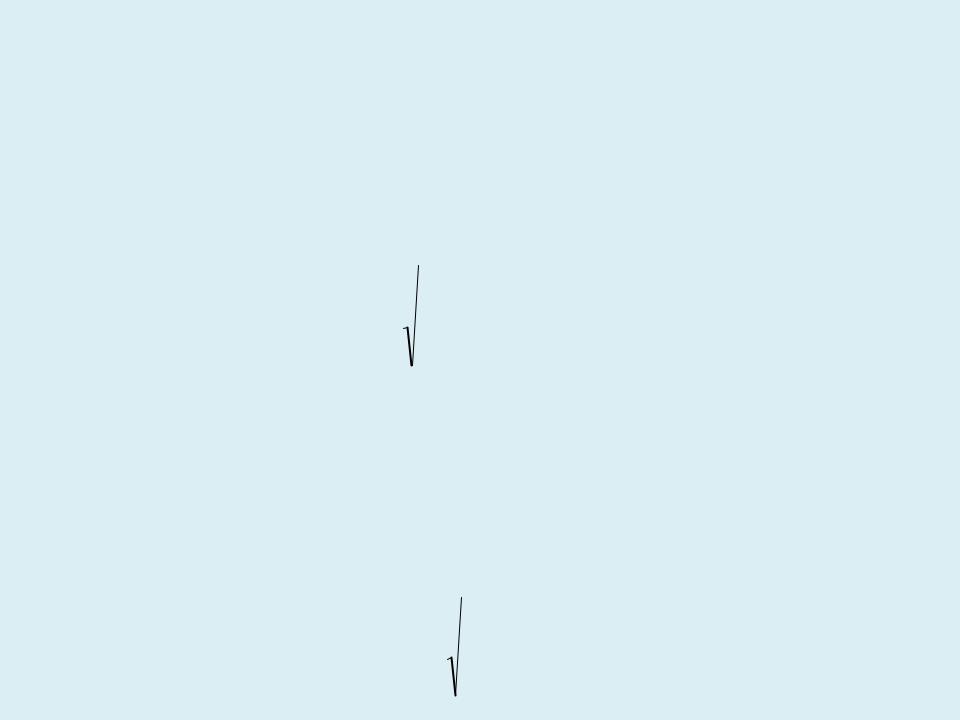
Последовательное соединение трубопроводов

1. Решение задач первого типа (заданы d, l и Q – определить напор H):

 

 

i n

li

 

 

l1

 

l2

 

ln

 

 

2

 

2

 

...

 

 

 

 

H Q

 

2

Q

2

 

2

2

 

 

.

 

 

i 1 Ki

 

 

K1

 

K2

 

Kn

 

2. Решение задач второго типа (заданы d, l и H – определить расход Q):

Q

 

H

 

 

 

.

i n

l

 

 

 

i

 

 

 

 

 

 

 

2

 

 

 

 

 

i 1

Ki

3. Задача третьего типа (заданы l, Q и H – определить d) определена, если ищется диаметр одного из участков трубопровода, а диаметры остальных участков известны. Тогда:

 

 

i n 1

l

 

 

l

 

 

H Q

2

 

 

i

 

 

m

 

где m – номер участка, диаметр которого неизвестен.

 

 

K

2

K 2

,

 

 

 

i 1

i

 

m

 

 

l

 

 

 

H

 

i n 1

l

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

lm

 

 

 

 

 

Тогда

 

m

 

 

 

 

 

i

 

,

Km

 

 

 

 

 

 

,

откуда определяем диаметр.

 

 

 

 

 

H

 

i n 1

 

 

2

 

2

 

2

 

 

K

m

 

Q

 

 

i 1

K

i

 

 

 

 

 

 

li

 

 

 

 

 

 

 

 

 

 

 

 

Q

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i 1

Ki

 

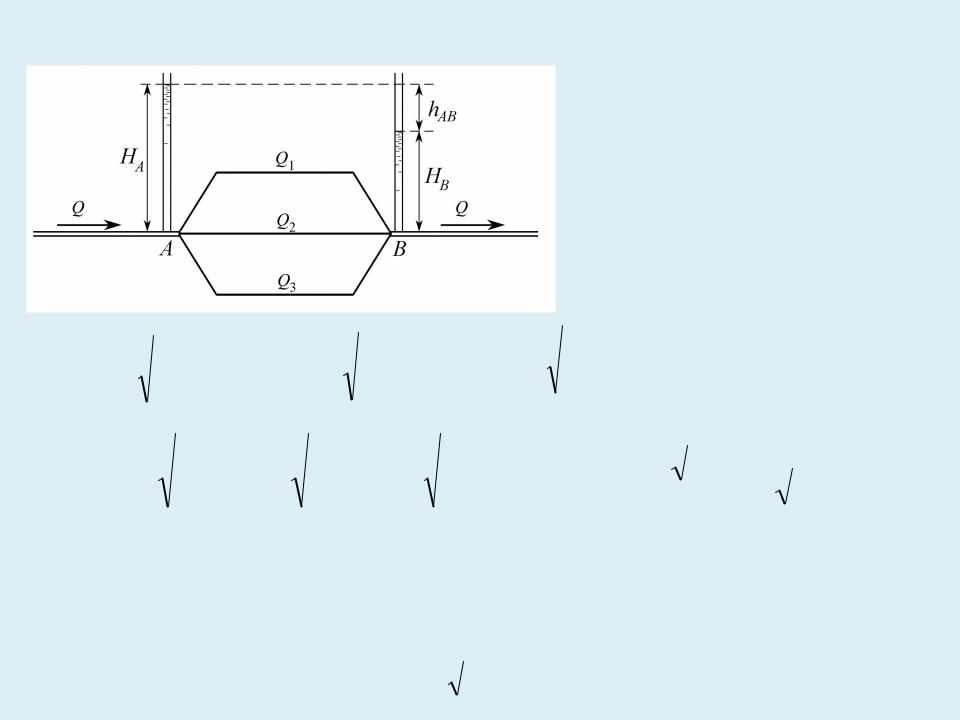
Параллельное соединение трубопроводов

hAB H A HB ,

hAB hпот 1 hпот 2 hпот 3.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

hAB

 

. Q Q Q Q .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

hAB

 

 

 

 

 

 

 

 

 

 

 

 

 

Q1 K1

hAB

 

 

,

 

Q2

K2

,

 

 

Q3

K3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

l1

 

 

 

 

l2

 

 

 

 

 

 

 

 

 

 

 

 

 

l3

1

2

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

Ki

 

 

 

 

 

h

 

 

 

 

h

 

 

 

 

 

 

 

 

 

 

h

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Q K1

 

 

AB

 

K2

 

 

AB

 

K3

AB

.

 

 

 

 

Q hAB

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

l

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

l

 

 

 

 

 

l

2

 

 

 

 

 

 

 

 

l

 

 

 

 

 

 

 

 

 

 

 

i 1

 

i

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Зная характеристики ветвей трубопровода Ki и li, а также суммарный расход

жидкости Q определяем потери напора между узлами A и B:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

hAB

 

 

Q2

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

K

i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

l

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i 1

 

 

i

 

 

 

 

 

 

 

 

 

 

 

 

 

Гидравлический расчет коротких трубопроводов

При расчетах коротких трубопроводов нельзя пренебрегать кинетической энергией потока в выходном сечении трубы

H h

вых вых2 .

пот

 

2 g

 

 

 

 

 

n

 

2

 

mi

 

 

2

 

hпот

тр i

i

 

 

 

i

 

 

2 g

 

мест j 2 g

.

 

 

i 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

j 1

 

 

 

 

 

 

 

 

 

 

Qi i i ,

 

 

 

 

i

 

 

Q2

 

n

 

mi

 

 

пр2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

hпот

 

2

 

тр i мест j

2

 

,

 

 

2 g пр i 1

 

 

j 1

 

i

 

 

 

Q1 Q2 ... Qi ... Qn Q.

 

Q

,

i

пр

пр .

 

 

i

 

 

 

 

 

 

 

i

 

 

 

 

 

 

Q2

 

n

 

 

 

 

 

 

 

 

H

 

2

 

тр i

 

2 g пр i 1

 

 

mi

 

2

 

 

пр

Q2

 

 

пр

 

 

 

.

мест j

 

 

 

 

 

2

 

 

2

j 1

 

i

 

2 g пр

Q

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

n

 

m

 

2

 

 

 

 

 

 

 

 

 

 

 

пр

пр

 

 

 

 

тр i мест j

2

 

 

 

i 1

 

j 1

 

i

 

 

Q пр пр 2 g H .

пр 2 g H ,

пр

 

 

1

 

 

 

 

 

.

 

 

 

 

 

 

 

 

n

m

 

пр2

 

 

 

 

 

 

 

 

 

 

тр i мест j

 

 

 

пр

2

 

 

 

j 1

 

 

 

 

 

 

 

i 1

 

i

 

 

 

 

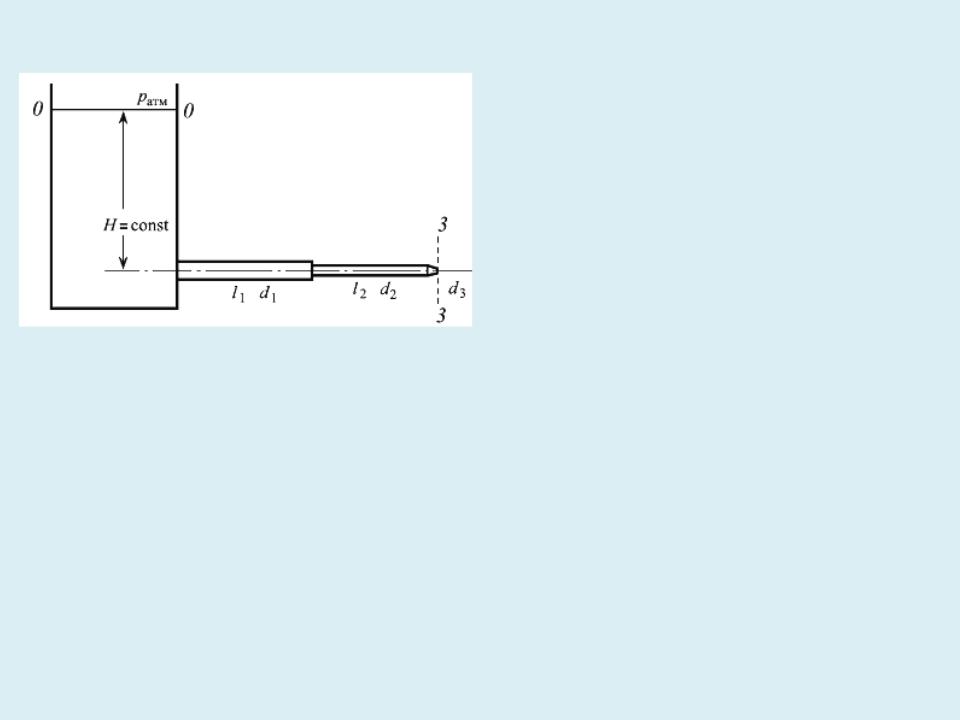
Пример расчета короткого трубопровода

 

 

 

2

p

 

 

 

2

p

 

 

0

 

0

0

z

0

 

3

3

3

z h .

 

 

 

 

2 g

 

g

 

2 g

 

g

3 пот

 

 

 

 

 

Уровень жидкости в резервуаре постоянен (H = const), значит 0 0,

 

3

32

p0 = pатм, p3 = pатм, z 0 = H, z 3 = 0.

Тогда

hпот .

H

 

 

2 g

 

 

 

Потери – на трение на 1 и 2 участках и местные сопротивления:

•вход в трубу из резервуара,

•внезапное сужение трубопровода на стыке первого и второго участков,

•конический насадок.

 

 

2

 

2

 

l

 

2

 

2

 

 

l

2

 

2

 

 

2

H

3

 

3

 

 

1

 

1

 

1

 

 

2

 

 

 

 

2

 

 

3

.

 

 

 

вх 2 g

d1

 

вн.с 2 g

 

d2

 

 

 

2 g

 

 

1

 

2 g

 

 

2

 

2 g

 

нас 2 g
Соседние файлы в папке Gidravlika_prezentatsii
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности