Неравномерное движение жидкости

в открытых руслах

Случаи неравномерного движения в открытых руслах

Неравномерное движение в открытых руслах устанавливается в следующих случаях:

в цилиндрических и призматических руслах (то есть имеющих вдоль течения одинаковое поперечное сечение) – в случаях устройства в русле плотины, перепада, щита или другого препятствия;

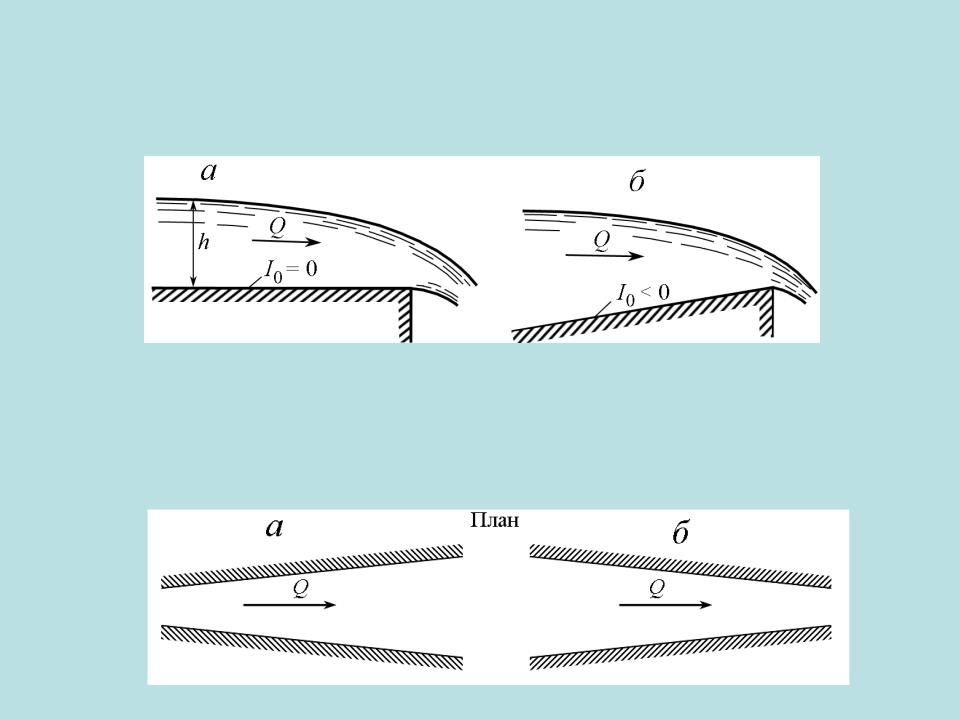
Случаи неравномерного движения в открытых руслах

• в руслах с горизонтальным дном (уклон I0 = 0) или с обратным уклоном (I0 < 0);

в нецилиндрических (непризматических) руслах, сечение которых изменяется по длине – расширяется, сужается или меняется произвольным образом.

Кривые свободной поверхности потоков

Важнейшей задачей расчета неравномерного движения является построение кривых свободной поверхности потоков.

Если глубина потока при неравномерном движении уменьшается вниз по течению, кривая свободной поверхности называется кривой спада.

Если глубина потока вниз по течению увеличивается, кривая свободной поверхности называется кривой подпора.

Нормальная глубина

Один и тот же расход Q может быть пропущен через русло (даже призматического сечения) при различном его наполнении, то есть при разных глубинах в каждом сечении. При больших глубинах вода будет двигаться с меньшей скоростью, при малых глубинах – с большей. Однако равномерное движение заданного расхода возможно только при одной глубине, определяемой формулой

Q K I0 ,

так как значению расходной характеристики (модулю расхода) K C R соответствует определенное значение глубины потока:

Нормальная глубина

Глубина равномерного движения потока жидкости h0 называется нормальной глубиной для данного расхода. Отвечающее нормальной глубине значение расходной характеристики K0 называется нормальной

расходной характеристикой. В заданном русле при всех глубинах, отличных от нормальной, заданный расход будет проходить при неравномерном режиме движения.

Каждому расходу в определенном русле соответствует свое значение нормальной глубины. Зная форму и размеры русла и расход жидкости, нормальную глубину можно определить графически. Для этого следует построить график зависимости K = f (h): задаваясь некоторыми значениями глубины h, можно вычислить соответствующие значения расходной характеристики K и по полученным точкам построить график

Затем на оси K следует отложить величину нормальной расходной характеристики

Q K0 I0

и на оси h определить соответствующее значение нормальной глубины h0.

Удельная энергия сечения

Удельной энергией сечения

называется удельная механическая энергия жидкости, рассчитанная относительно плоскости сравнения, проведенной через низшую точку сечения – плоскость O–O.

Критическая глубина

Э h 2 .

2 g

Глубина, при которой удельная энергия сечения достигает минимального значения Эmin, называется критической глубиной hкр.

Критическая глубина

Определяется критическая глубина из условия минимума удельной энергии сечения Э

По этой формуле можно определить критическую глубину для русла любого сечения.

кр , Bкр – площадь живого сечения и ширина

его по верху при критической

глубине hкр