Добавил:

neus500 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский авиационный институт (национальный исследовательский университет)

Предмет:

Теория функций комплексного переменного

Файл:

ТФКП лекции Гурина Т.А

..pdf

Скачиваний:

Добавлен:

24.07.2017

Размер:

883.39 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

1.4. Основные элементарные функции и их свойства

1.4Основные элементарные функции и их свойства

1.4.1Линейная функция

w = az + b, где a, b = const C.

Линейная функция обратима: z = a1 w − ab , a 6= 0; ∞ 7→ ∞; C ↔ C.

Утверждение 1. Линейная функция является последовательностью растяжения, поворота и сдвига.

Доказательство. Растяжение: w1 = |a|z; поворот: w2 = w1ei arg a, (a = |a|ei arg a);

сдвиг: w = w3 = w2 + b.

Утверждение 2. Линейное отображение обладает круговым свойством (окружность переходит в окружность, прямая - в прямую).

Доказательство. z − z0 = Reit, t [0, 2π];

z = a1 w − ab , z0 = wa0 − ab a1 w − a1 w0 = Reit, w − w0 = |a|Rei(t+arg a) - точки окружности.

z − z0 = teiϕ, t R+; a1 w − a1 w0 = teiϕ

w − w0 = t|a|ei(ϕ+arg a) - прямая.

Утверждение 3. Линейное отображение является преобразованием подобия.

Доказательство. Очевидно.

1.4.2Обратная функция

w = z1; 0 7→ ∞; ∞ 7→0, z = w1 ; C → C

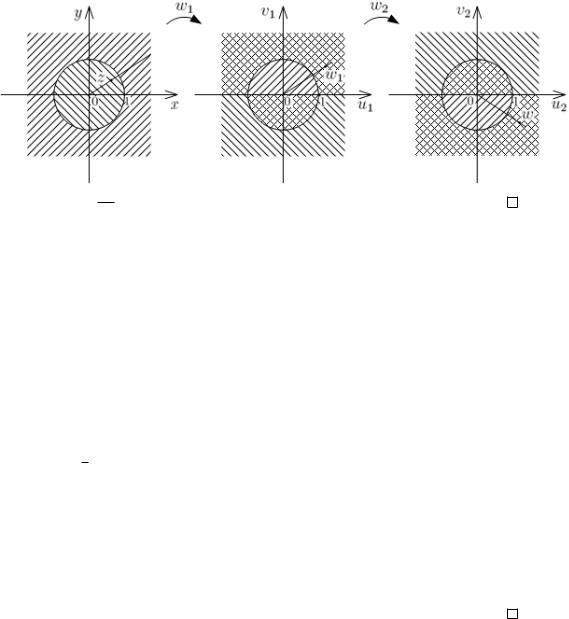
Утверждение 1. Обратное отображение является последовательностью инверсии и отражения.

Доказательство. w1 = z ; w2 = w1;

w1 - симметричное отражение относительно единичной окружности.

22	Глава 1. Введение в комплексный анализ

|z| · |w1| = |z||z| = 1; arg w1 = arg z

Утверждение 2 (Круговое свойство). Окружности и прямые, проходящие через точку z = 0, переходтят в прямые, а точки, не проходящие через z = 0, переходят в окружности.

Доказательство.

A(x2 + y2) + Bx + Cy + D = 0;

x2 + y2 = zz,

z +

x =

y =

Azz +

2 + 2i z +

−

2i z + D = 0;

z =

, тогда

− 2i w + D = 0,

Aww +

+ 2i w + 2

− 2i w +

Dww +

+ 2i w + A = 0.

Утверждение 3 (Сохранение симметричных точек). Пусть z1 и z2 - симметричные точки.

|z1| · |z2| = R2,

1		·		1		= R2
\|w1\|			\|w2\|

1.4. Основные элементарные функции и их свойства

1.4.3Дробно-линейная функция

w =

az + b

;

cz + d

b − dw

ad = cb; z =

;

−c

−

7→ ∞ ∞ 7→c

Утверждение 1. Дробно-линейная функция является последовательностью

линейной, обратной и линейной функций.

Доказательство.

w =

c(az + b)

a(cz + d) + bc − ad

bc − ad

;

c(cz + d)

w1 = cz + d, w2 =

, w3 =

bc − ad

w2 +

Утверждение 2. Для дробно-линейной функции характерны круговое свойство и свойство сохранения симметрии точек (см. выше)

Утверждение 3 (Отображение 3-х точек).

z1, z2, z3 C и w1, w2, w3 C

az + b

! w = f(z) = cz + d, w(zj) = wj, j = 1, 2, 3.

Доказательство.
f1 : z1 7→0, z2 7→1, z3 7→ ∞,
f	(z) =	z − z1	z2 − z3	;
1		z − z3	· z2 − z1

f2 : w1 7→0, w2 7→1, w3 7→ ∞,
f	(w) =	w − w1	w2 − w3	.
2		w − w3	· w2 − w1

24			Глава 1. Введение в комплексный анализ
f(z) = f2−1 f1(z)	f1(z) = f2(w)
		w − w1	w2 − w3	=	z − z1		z2 − z3	;
		w − w3	· w2 − w1
				z − z3		· z2 − z1

Единственность доказывается от противного.

Замечание. Формула трех точек работает и в случае бесконечно удаленных точек, при этом отношения, содержащие бесконечно удаленную точку в числителе и знаменателе, заменяются единицей.

Пример. Написать дробно-линейную функцию, отображающую единичный круг на верхнюю полуплоскость.

Z = {|z| < 1}, W = {Im w > 0}.


z1		= 0	7→w1		= i;
z2		= 1	7→w2		= 0;
z3 = ∞ 7→w3 = −i;
	w − i			0 + i	=	z − 0		1 − ∞	;
					=				;
	w + i		·	0 − i		z − ∞	·	1 − 0
		w − i		= z;
−w + i				= z;
−w + i

1.4. Основные элементарные функции и их свойства

−ww −+ ii = z;

w − i = −z(w + i), w + wz = i − iz;

w = −iz + i. z + i

1.4.4Степенная функция и радикал

w = zn, n Z+.

√

z = n w.

w = z2, z = sqrtw

Замечание (Поверхность Римана).

Пример (Функция Жуковского).


1				1				z2 + 1
w =			z +				=2		;
	2					z		2z
w + 1				z + 1
w − 1		=			z − 1			;

z= reiϕ, z1 = 1r e−iϕ;

	1	1		e−iϕ		1		1	(cos ϕ − i sin ϕ);
w =		reiϕ +			=		r(cos ϕ + i sin ϕ) +
	2		r			2		2r

26	Глава 1. Введение в комплексный анализ

w = u + iv;

u =	1	r +	1		cos ϕ,
	2			r

	1	1
v =		r −		sin ϕ;
	2		r

1.4.5Экспонента и логарифм

Определение 1.

ez := lim 1 + z n

n→∞ n

Утверждение 1. ez = ex (cos y + i sin y)

Доказательство. Найдём |ez| −?

1 +

x + iy

1 +

n/2

+ i

1 +

2x x2 + y2

n/2

1 +

при

→ ∞

это эквивалентно

1 +

2x n/2

ex,

при

Таким образом, |ez| = ex.

→

→ ∞

Найдём arg(ez)−?

= n arctg

n +

arg 1 − n

= n arg

+ n

+ in

1 + x

= y, при n → ∞

1.4. Основные элементарные функции и их свойства

Таким образом, arg ez = y. Следовательно, ez = ex (cos y + i sin y)

Утверждение 2. ez1+z2 = ez1 · ez2

Доказательство.

ez1 · ez2 = ex1 (cos y1 + i sin y1) · ex2 (cos y2 + i sin y2) =

= ex1 ex2 (cos (y1 + y2) + i sin (y1 + y2)) = ez1+z2

Утверждение 3. ez – периодическая функция. Период T = 2πi

Доказательство.

ez+T = ez, eT = 1, T = T1 + iT2

eT (cos T2 + i sin T2) = e0 (cos 2π + i sin 2π)

T1 = 0, T2 = 2πk, T = i 2πk, T = i 2πk

Утверждение 4. eiz = cos z + i sin z Формула Эйлера.

Доказательскво позже.

Утверждение 5.

z= x + i 0

z= x + i 2π

z	x		x
w = ez	= ex	(cos 0 + i sin 0)	= ex
w = e	= e	(cos 2π + i sin 2π)	= e

Определение 2. Натуральный комплексный логарифм, обратный z = ew, обозначается w = ln z.

28	Глава 1.	Введение в комплексный анализ
Утверждение 1. Из того, что		arg w 6= 0 следует что
	0 < Im z < 2π
Утверждение 2. ln(z1 · z2) = ln z1 + ln z2
Доказательство.
z1 · z2 = eln(z1·z2), z1 = eln z1 , z2 = eln z2 , eln z1 · eln z2 = eln z1+ln z2 = z1 · z2
Утверждение 3. ln z = ln \|z\| + i arg z
Доказательство.
z = \|z\|ei arg z,	ln z = ln \|z\| + ln ei arg z = ln \|z\| + i arg z

Замечание. Многозначный логарифм

Ln z = ln z + i Arg z = ln |z| + i arg z + i πk, k = 0, ±1, ±2, ...

1.4.6Тригонометрические функции и обратные к ним

ei z = cos z + i sin z,			e−i z = cos z − i sin z,
cos z :=	ei z + e−i z	,	sin z :=	ei z − e−i z	.
	2
				2 i

Утверждение 1. cos z является композицией линейной функции, экспоненты, функции Жуковского.

	1	1
Доказательство. w1 = i z, w2 = ew1 , w3 =		w2 +
	2		w2

1.4. Основные элементарные функции и их свойства

Утверждение 2.

sin z

tg z := cos z; T = π

Определение 1. Арккосинус z – функция обратная к z = cos w обозначается w = arccos z

√

Утверждение 1. arccos z = −i ln z + z2 − 1 .

Доказательство.

e2 i w

2z ei w

× 2

ei w

√z2

i w,

z = ei w+e−i w

− 2

1 = 0 ln +

− 1 =

1 .

ei w = z + √z

w = i ln z +

√z2

−

Замечание. Многозначный арккосинус

√

Arccos z := −i Ln z + z2 − 1

Упражнение. Дать утверждения для arcsin z, arctg z.

30	Глава 1. Введение в комплексный анализ

1.4.7Гиперболические функции и обратные к ним

ch z :=

−z,

T = 2πi

+ e z

−

e−

sh z

sh z2 i

th z

T = πi

ch z

Замечание. w = arcch z обратна к z = ch w

ew+e−w

√

+ 1 = 0,

− 1

− 2ze

arcch z = ln z + √z

z =

w = ln z + z

− 1 ,

= +

− 1

Arcch

−

√

Ln z + √

1 .

Упражнение. Вывести arcsh z, arcth z.

Упражнение. Рассмотреть отображение комплексной плоскости функцией ch z.

1.5Комплексное интегрирование

Определение 1 (Интеграл комплексной функции действительного переменного).

g : [t1, t2] 7→ C, g(t) := g1(t)+i g2(t), g(t) C ( ) , g1,2 : [t1, t2] 7→R

t2 t2

Z Z Z

g(t) dt := g1(t) dt + i g2(t) dt

t1 t1

Определение 2 (Интеграл комплексной функции комплексного переменного).

f : → C, C, γ(t) : [t1, t2]0 7→ , γ(t) C1 [t1, t2]

f(z) dz := f γ(t) γ0(t) dt

Определение 2’ (Интеграл комплексной функции комплексного переменного).

Z		k−1
Z	( )	:= µ→0 j=0	j	j
	z	X	f (ξ ) z ,
f	z	dz lim	f (ξ ) z ,
zj	= zj+1 − zj, µ = max \|			zj\|

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в предмете Теория функций комплексного переменного

#
24.07.2017221.7 Кб65tfkp(kratko).doc
#
24.07.2017883.39 Кб87ТФКП лекции Гурина Т.А..pdf