П2

Практическое занятие 2.4

Расчет статически неопределимых плоских рам

Для снятия статической неопределимости плоских рам придерживаются следующего порядка

1. Устанавливают степень статической неопределимости (число лишних связей).

2. Удаляют лишние связи, заменяем исходную систему статически определимой, которая называется основной системой

3. Загружают основную систему.

4. Приравнивают к нулю перемещения точек приложения неизвестных реакций по направлению их действия.

5. Из полученного уравнения определяют неизвестное усилие.

6. Выполняют проверку правильности решения задачи по снятию статической неопределимости плоской рамы.

Для примера рассмотрим статически неопределимую плоскую раму, показанную на рис.1, а, для которой ; ; ;

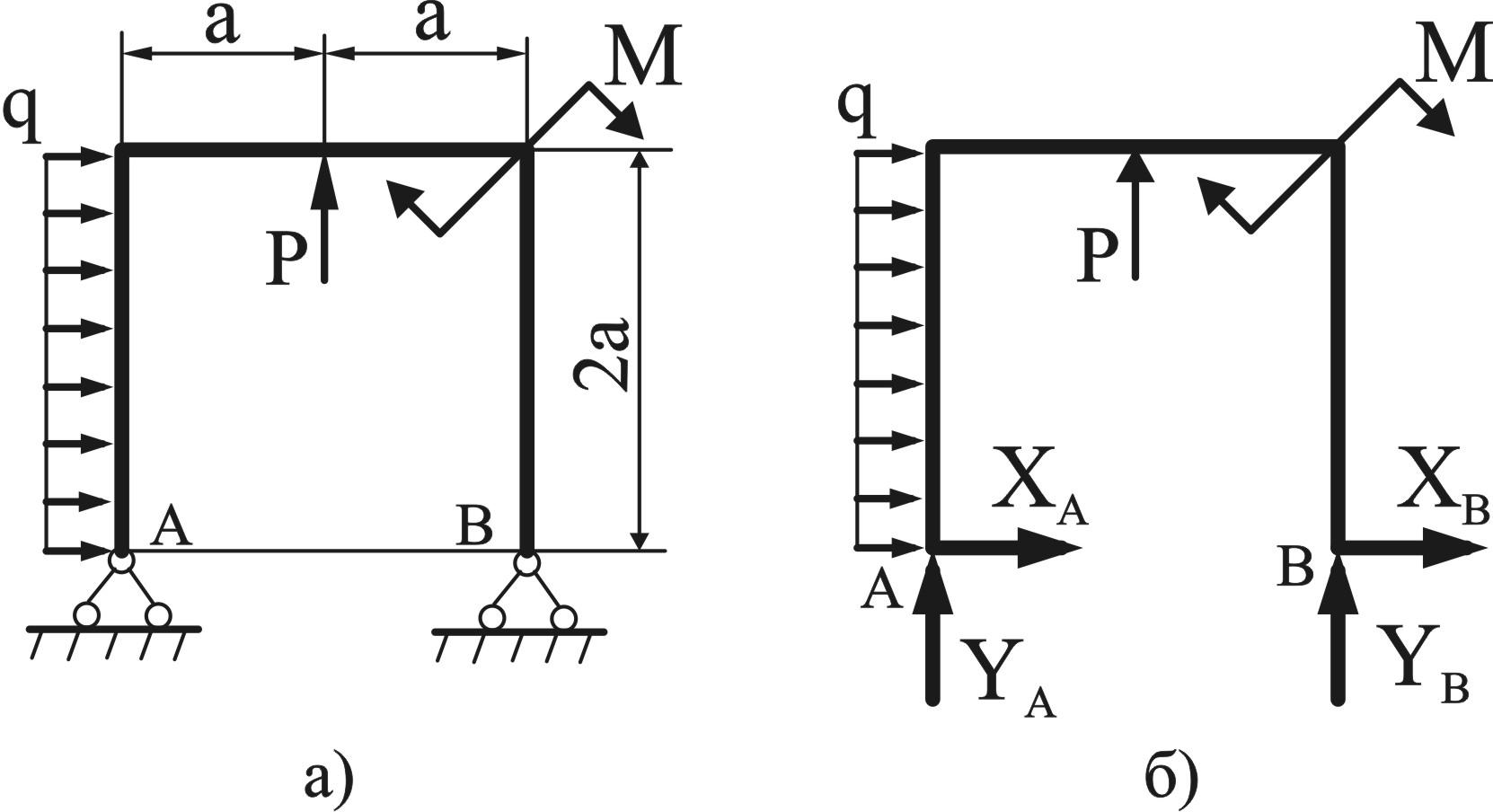
рис. 1

1. Опоры А и В дают четыре реакции (рис.1,б). Для плоской системы сил мы можем составить только три уравнения равновесия, поэтому заданная расчетная рама является один раз статически неопределимой.

2. Для построения основной системы нужно устранить одну связь. Для исключения лишней связи заменим неподвижный шарнир в точке В вертикальным стержнем (Рис. 2)

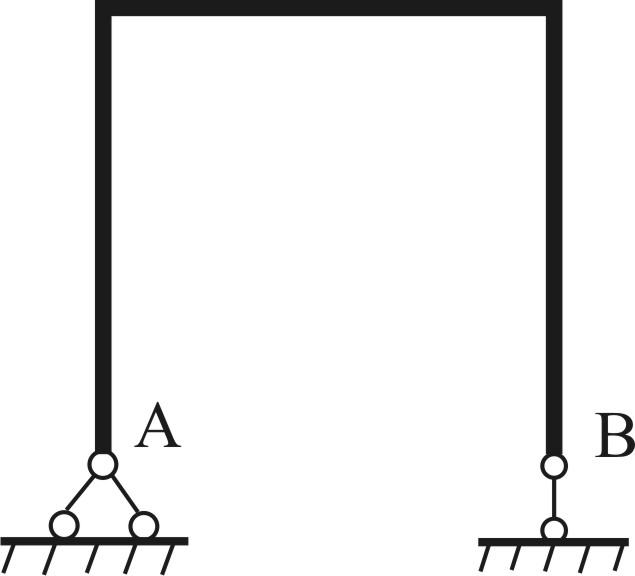
рис. 2

3. Для получения эквивалентной системы загружаем основную систему заданной нагрузкой и лишним неизвестными усилием (рис.3)

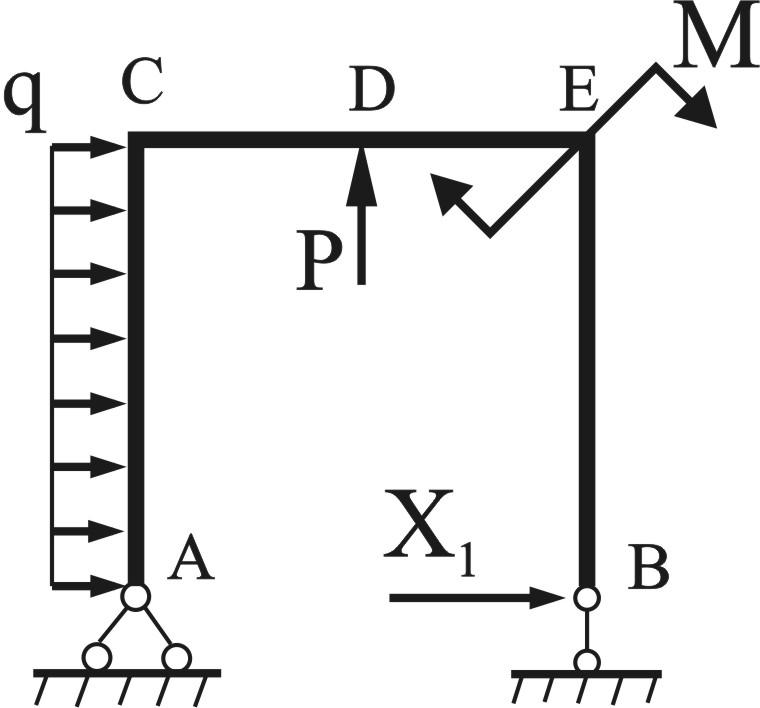
рис. 3

4. Полное перемещение точки В основной системы (от заданной нагрузки и лишнего неизвестного усилия) по направлению удаленной связи должно быть равно нулю. Полное перемещение можно представить как сумму перемещений от внешней (рабочей) нагрузки и неизвестной реакции .

Перемещение от неизвестной реакции можно представить произведением реакции на удельное перемещение точки В в направлении действия от единичной силы . Тогда

.

Для определения перемещений и рассматриваем основную систему, отдельно нагруженную заданной нагрузкой (q, M и Р) (Рис. 4) и единичной силой (Рис. 5).

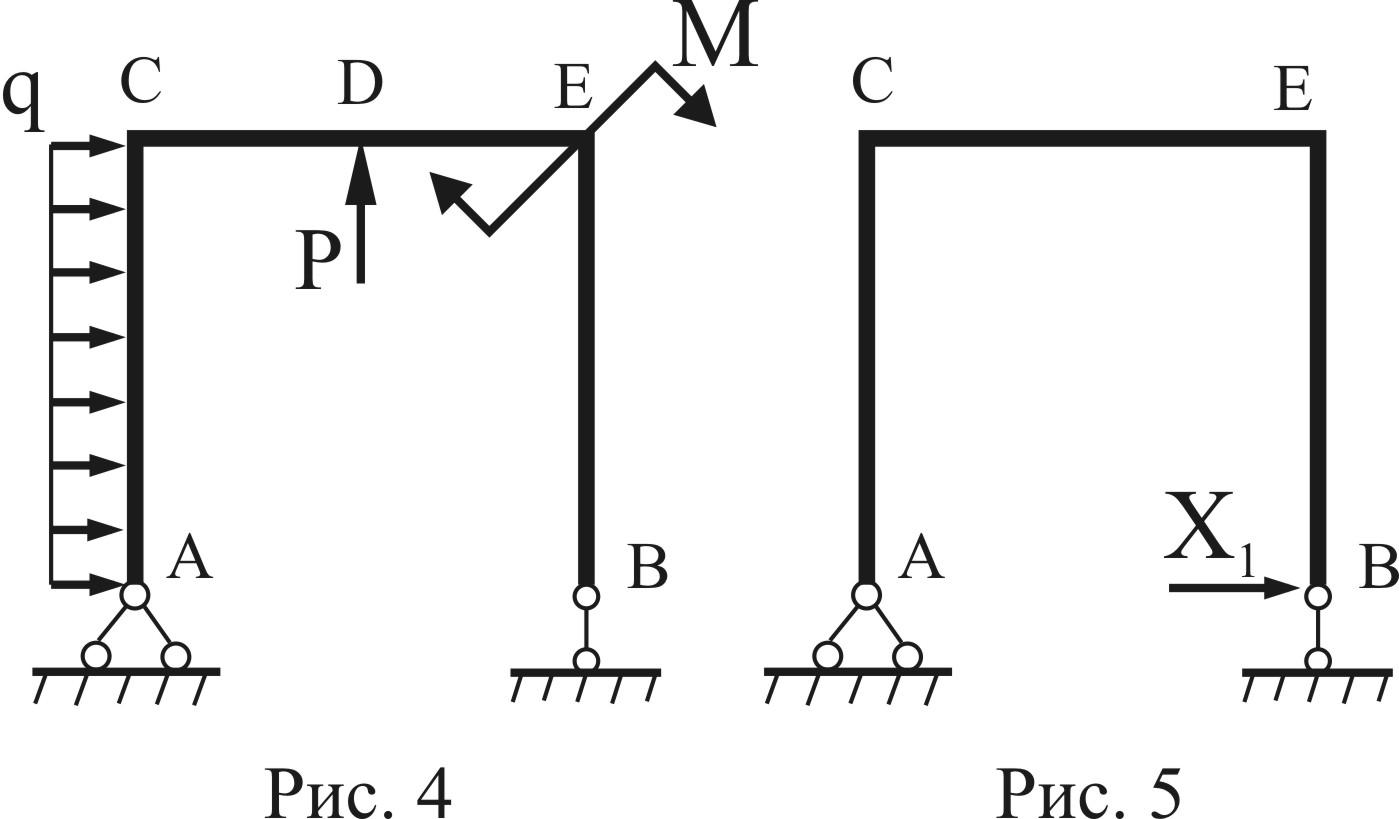
Для нахождения перемещений применяем способ Верещагина. Для этого необходимо построить эпюры изгибающих моментов для основной системы, нагруженной рабочей нагрузкой и единичной силой .

4.1. Эпюра . Определяем опорные реакции (Рис. 6).

рис. 6

;

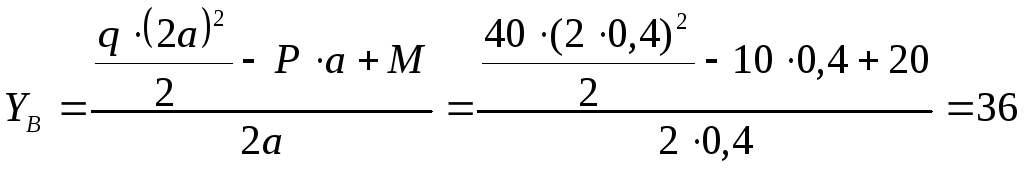, кН

;

, кН

;

, кН

Для проверки правильности определения реакций опор составим уравнение моментов относительно точки приложения силы :

;

Для построения эпюры «» будем вычислять величины изгибающих моментов на участках , , и .

Очевидно, что в точке : .

Очевидно и то, что в любом сечении стержня : .

Для участка зависимость изгибающего момента будет линейной.

В точке :

В точке :

Для участка зависимость изгибающего момента также будет линейной.

В точке :

В точке :

На участке зависимость изгибающего момента будет нелинейной.

Для проверки наличия экстремума изгибающего момента определим поперечную силу для границ участка.

Для точки

Для точки

Поперечная сила на участке не меняет знак, значит, на эпюре моментов внутри участка не будет экстремума

Выражение момента на участке

Для точки

Определим значение момента для середины участка

Строим эпюру моментов для рабочей нагрузки на сжатых волокнах рамы (Рис. 8, а).

4.2. Эпюра . Нагружаем основную систему единичной силой (Рис. 7).

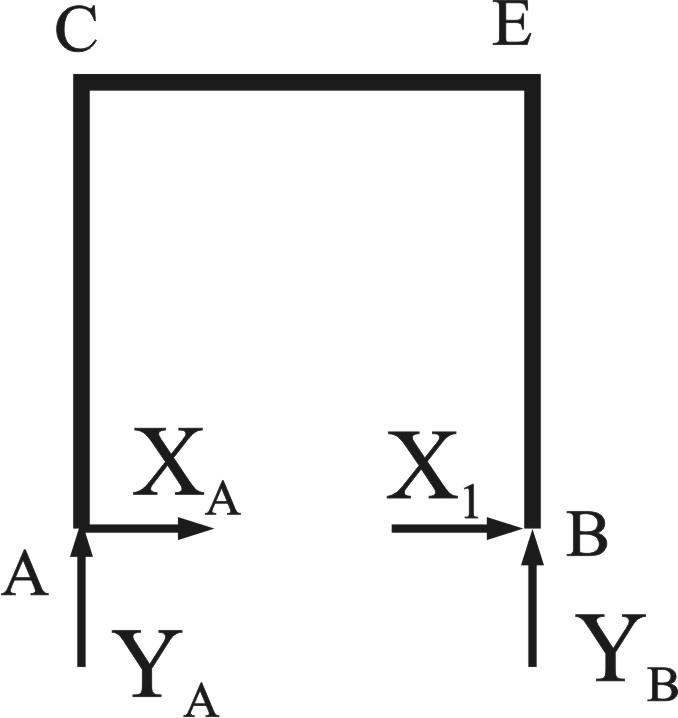
рис. 7

Определяем реакции опор.

На всех участках эпюра единичных моментов будет прямолинейной.

В точке : .

В точке : .

В точке : .

Строим эпюру единичных моментов (Рис. 8, б).

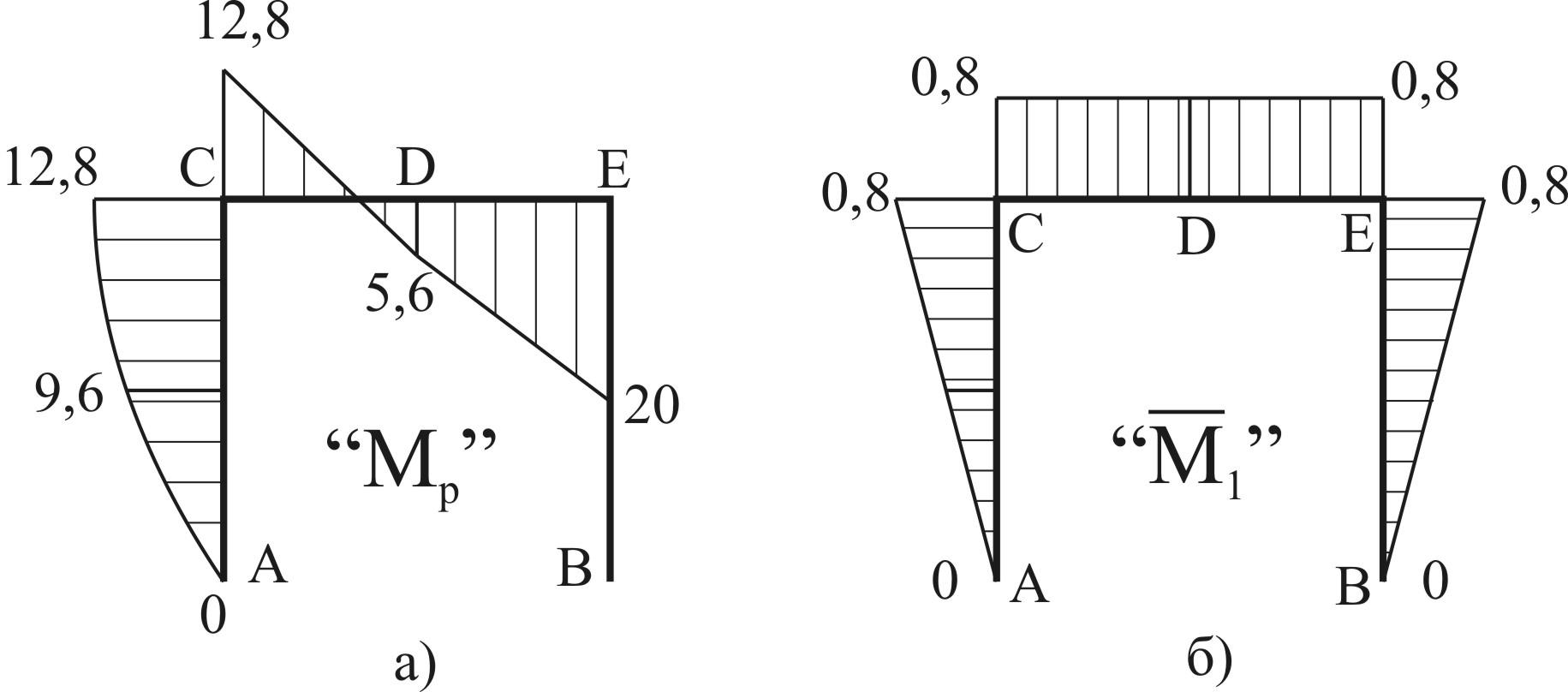
рис. 8

4.3 Определяем перемещения.

Перемещение точки В от заданной загрузки.

,

Где - часть площади эпюры моментов от заданной нагрузки, для которой легко можно определить площадь и положение центра тяжести фигуры.

- ордината эпюры моментов от единичной нагрузки, расположенная под центром тяжести части площади эпюры моментов от внешней нагрузки.

- жесткость рамы.

Разбиваем площадь эпюры моментов от внешней эпюры на части

На участке раскладываем площадь эпюры на треугольник и параболу .

Площадь треугольника

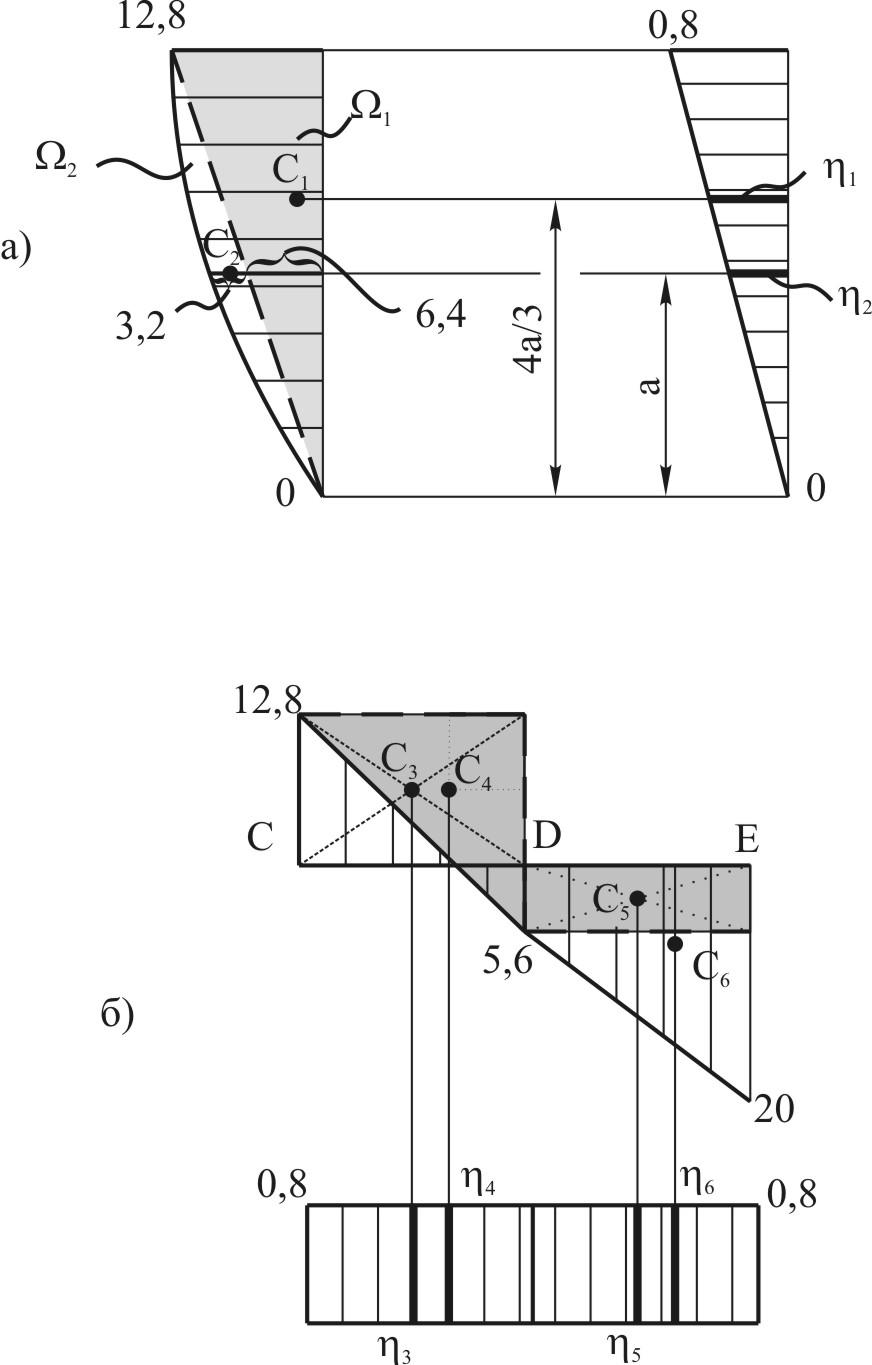
рис. 9

Центр тяжести прямоугольного треугольника находится на расстоянии одной третей катета от прямого угла

Площадь параболы ,

где - высота параболы.

Данная парабола симметрична середине участка . Там же будет находиться центр тяжести параболы.

На участке рассматриваем площадь эпюры как сумму положительной площади прямоугольника и отрицательной площади треугольника .

Площадь прямоугольника

Площадь треугольника

На участке раскладываем площадь эпюры на прямоугольник и треугольник .

Площадь прямоугольника

Площадь треугольника

Определяем ординаты эпюры моментов от единичной нагрузки.

;

;

Находим произведение площадей на соответствующие координаты

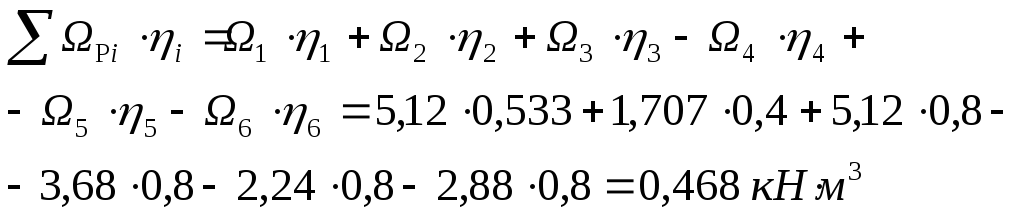
Если эпюры моментов от внешней и единичной нагрузки направлены в одну сторону, то произведение входит в уравнение со знаком плюс.

Перемещение получаем аналогичным перемножением эпюры на эпюру

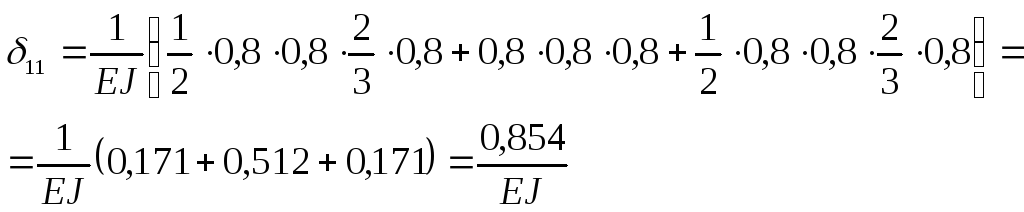
4.4 Полное перемещение

Откуда

Таким образом, реакция отброшенной опоры .

5. Для проверки правильности раскрытия статической неопределимости будем использовать статическую и деформационную проверки. Для статической проверки необходимо построить эпюры внутренних силовых факторов и проверить статическую уравновешенность произвольного узла.

5.1. Для заданной системы определяем реакции опор (рис. 1,б).

Реакция Х_В уже определена . Составляем уравнения равновесия для определения остальных реакций.

;

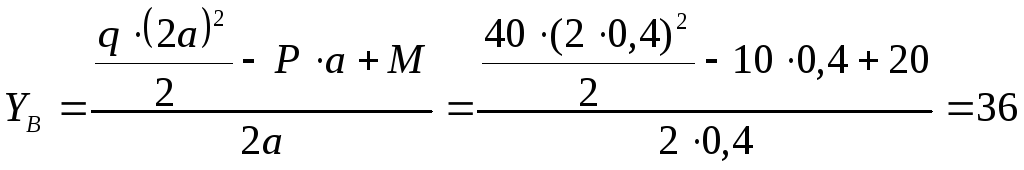, кН

;

, кН

;

, кН

Для проверки правильности определения реакций опор составим уравнение моментов относительно точки приложения силы :

;

5.2 Определяем внутренние силовые факторы на участках

Участок АС

Продольная сила

Поперечная сила

В точке А

В точке С

Поперечная сила будет равна нулю в сечении с координатой равной

Изгибающий момент

В точке А

В точке С

По середине участка

В сечении, для которого поперечная сила равна нулю

Участок СD

Участок DЕ

Участок ВЕ

5.3 Строим эпюру моментов (рис. 10) и выполняем деформационную проверку.

рис. 10

Деформационное условие выполняется. Строим эпюры продольных и поперечных сил (рис. 11).

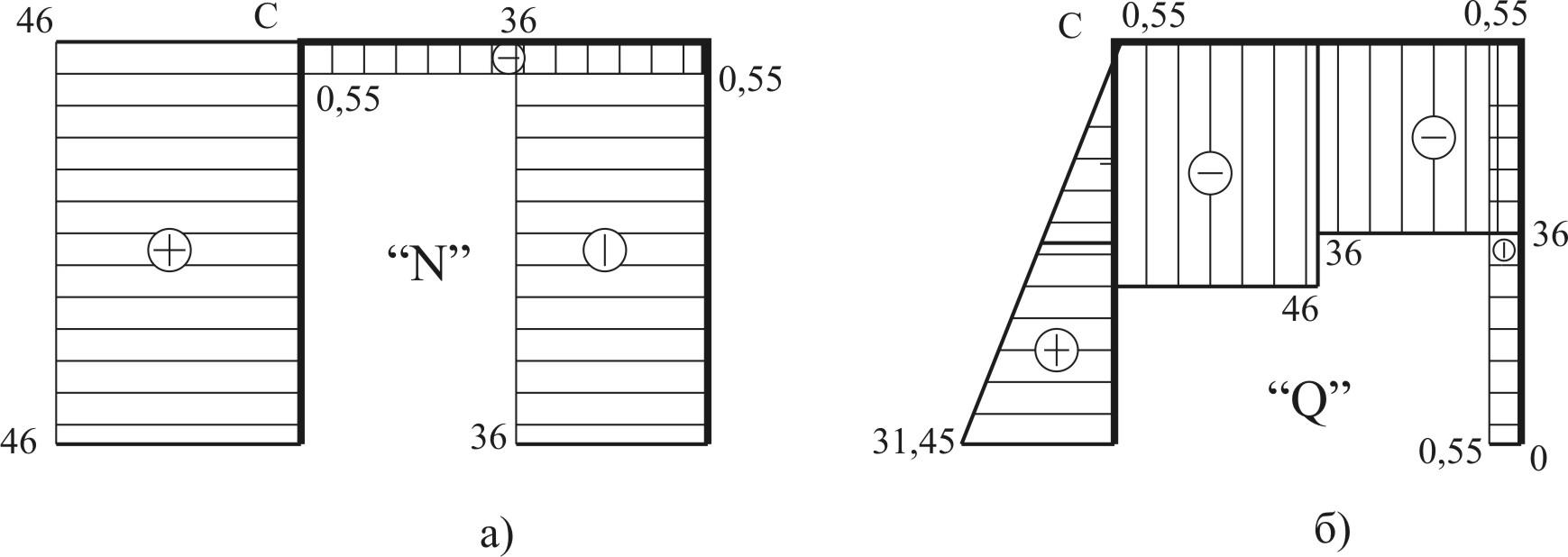
рис. 11

5.4 Выполним статическую проверку. Для этого вырезаем узел С и рассматриваем условие равновесия (рис. 12).

Снизу на узел С действует изгибающий момент , поперечная сила , продольная сила

Справа от узла С действует изгибающий момент , поперечная сила , продольная сила

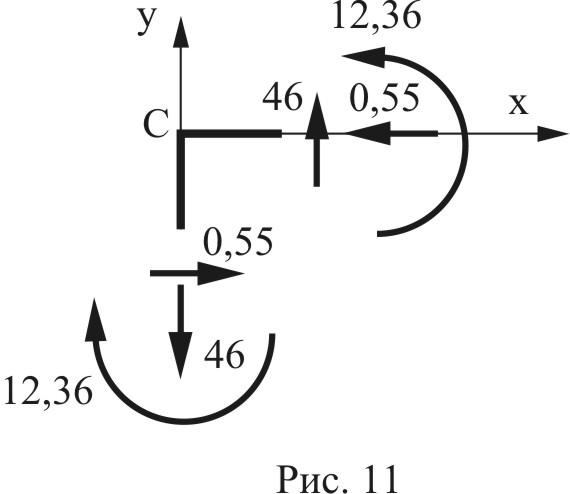
рис. 12

Поперечная сила и поперечная сила приложены на бесконечно малом расстоянии от точки С, поэтому момент от этих сил относительно точки С будет равен нулю. В уравнение моментов в данном случае войдут только изгибающие моменты.

Статическая и деформационная проверки выполнены. Решение статически неопределимой системы правильное.