
пример_метод_перемещений
.pdf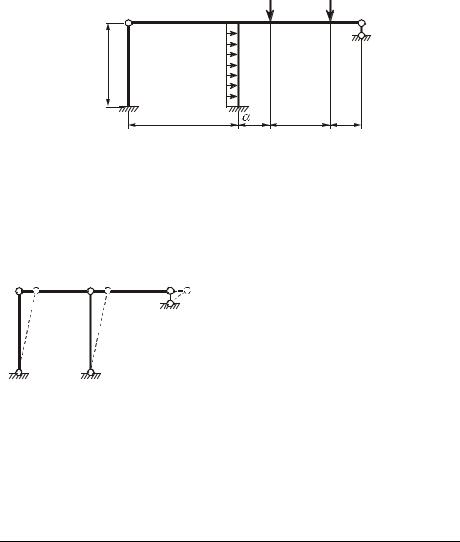
Пример расчета рамы методом перемещений |
1 |
ПРИМЕР РАСЧЕТА РАМЫ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Задана статически неопределимая рама (рисунок 1), у которой l = 4 ì; h = 3 ì; α = 1,2; k = 0,7; P = 24 êÍ; q = 13 кН/м. Требуется построить эпюры изгибающих моментов Ì, попереч- ных Q и продольных сил N; выполнить необходимые проверки.
P P
h
k EJ
EJ |
|
|
q |
EJ |
|
k |
||
|
l |
l/4 |
|
Рисунок 1 |
EJ
 l/2
l/2  l/4
l/4
Определение количества неизвестных. Вычислим степень кинематической неопределимости по формуле: n = nóB B + nëB ,B ãäå nóB B – число неизвестных углов поворота узлов; nëB B – число неизвестных независимых линейных перемещений узлов.
Заданная система имеет один жесткий узел, поэтому nóB =B 1. Для вычисления nëB B преобразуем раму в шарнирную схему (рисунок 2) и определим число ее степеней свободы (Ø = 7 – число простых шарниров; Ê = 2 – число замкнутых контуров):
WøP .ñ.P = Ø – 3Ê = 7 – 3 · 2 = 1.
Следовательно, nëB B = WøP .ñ.P = 1.
Шарнирная схема представляет
собой геометрически изменяемую
систему с одной степенью свободы,
точки которой могут свободно дви-
гаться по горизонтали.
Степень кинематической неопределимости n = 1 + 1 = 2.
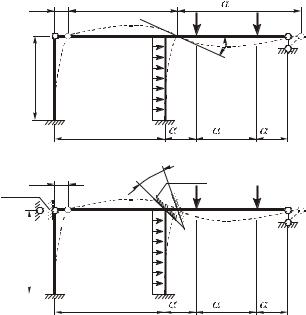
Выбор неизвестных. Под действием нагрузки заданная система деформируется, ее жесткий узел K поворачивается на угол Z1B ,B à óçëû Â, K, Ñ смещаются по горизонтали на одну и ту же величину Z2B B (рисунок 3). Перемещения Z1B ,B Z2B B будут неизвестными метода перемещений.
Формирование основной системы. Вводим плавающую заделку (связь 1) в жесткий узел рамы и горизонтальный опорный стержень (связь 2). Для компенсации дополнительных связей
Яровая А. В. www.mechanika.org.ru
2 |
Пример расчета рамы методом перемещений |
основной системе необходимо придать угол поворота Z1B B и линейное смещение Z2B ,B имеющиеся в заданной системе (рисунок 4).
Z2 |
l |
|
l |
|
|
|
|
|
|
P |
EJ |
P |
C |
|
B |
EJ |
K |
Z1 |
|
|
|
|
|
|
|
|
|
|
k EJ |
|
q |
|
|
|
h |
Заданная |
kEJ |
|
|
|
|
|
A |
система |
D |
|
|
|
|
|
|
|
|
||
|
|
l |
l/4 |
l/2 |
l/4 |
|
|
|
Рисунок 3 |
|
|
|
|
Z2
Связь 2
|
|
|
|
|
h |
|
EJ |
|
|
|
|
|||
|
|
|||
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
Z1
Связь 1
P EJ P
EJ |
|
|
q |
Основная |
kEJ |
система |
|
l |
|
l/4 |
l/2 |
l/4 |
|
||||
|
|
|
|
|
Рисунок 4
Запись системы канонических уравнений. Рама два раза кинематически неопределима, значит, будет два уравнения:
r11B ZB 1B B + r12B ZB 2B B + R1pB B = 0;
r21B ZB 1B B + r22B ZB 2B B + R2pB B = 0,
ãäå ZiB B – неизвестное перемещение по направлению i-ой введенной связи; rijB B – реакция в i-ой связи от единичного перемещения j-ой связи; RipB PB –P реакция i-ой связи от внешней нагрузки.
Отметим, что r11B ,B r12B ,B R1B pB представляют собой моментные реакции связи 1; r21B ,B r22B ,B R2B p–B силовые реакции связи 2. При этом riiB B являются главными единичными реакциями; rijB B (i ≠ j) – ïî-
бочными; rijB B = rjiB .B
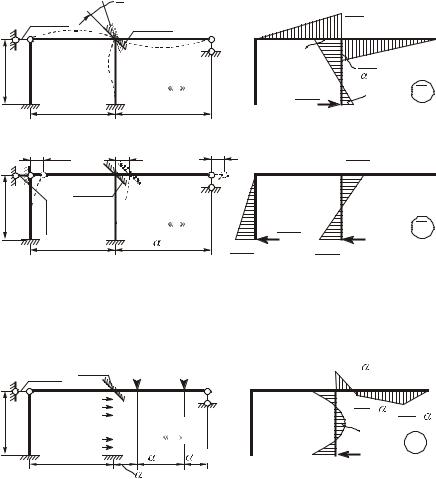
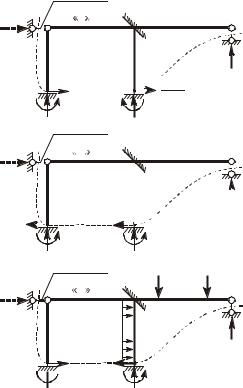
Построение эпюр изгибающих моментов. Рассматриваем деформирование основной системы в результате поворота связи 1 на единицу (рисунок 5). Исполüçуя таблицы, строим единичную
эпюру изгибающих моментов |
M1 |
. Сразу же отмечаем значение |
опорной реакции в несмещающейся заделке. |
||
|
|
|
Яровая А. В. |
|
www.mechanika.org.ru |
Пример расчета рамы методом перемещений |
3 |
Исследуем деформирование основной системы в результате единичного горизонтальногî перемещения связи 2 (рисунок 6). Строим единичную эпюру M2 . Отмечаем значения опорных реакций в несмещающихся заделках.
h
Связь 2
EJ
k EJ
l
 Z1= 1
Z1= 1
|
Связь 1 |
EJ |
|
|
|
EJ |
Состояние |
|
k |
|
1 |
|
|
|
 l
l
|
3EJ |
|
|
l |
|
4kEJ |
3EJ |
|
h |
|
|
l |
|
|
|
|
|
6kEJ |
2kEJ |
Ì1 |
2 |
h |
|
h |
|
|
Рисунок 5
|
Z |
2= 1 |
1 |
1 |
6kEJ |
h2
h
k EJ
âÑ çÿ  2ü
2ü
EJ Связь 1
k EJ

l
EJ |
|
|
|
|
Состояние |
|
|
|
|
2 |
|
3kEJ |
|
12kEJ Ì2 |
l |
3kEJ |
h3 |
6kEJ |
h3 |
|
|
|
||
|
h2 |
|
h2 |
|
Рисунок 6
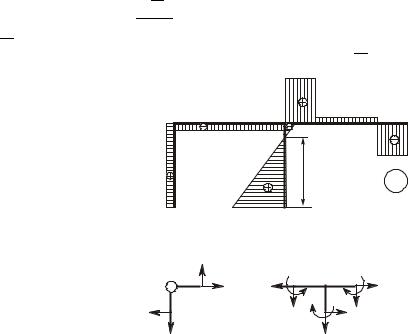
Прикладываем к основной системе только внешнюю нагрузку (рисунок 7). Пользуясь таблицами, для отдельных статически неопределимых балок строим эпюры изгибающих моментов.
Изобразив их на общей базе, получаем эпюру ÌðB .B |
9 |
|
|||
Связь 2 Связь 1 P |
|
P |
P l |
||
|
|
32 |
|||
h
k EJ
EJ
l
q

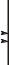 k EJ
k EJ
EJ |
|
qh2 |
5 P l |
23 |
|
|
|
|
12 |
P l |
|||
Состояние |
128 |
128 |
||||
|
qh2 |
|
||||
|
|
|
||||
p |
|
qh2 |
24 |
Ìp |
||
l/2 |
l/4 |
|||||
12 |
qh/2 |
|
|
|||
l/4 |
|
|
|
|||
|
|
|
|
|
||
Рисунок 7
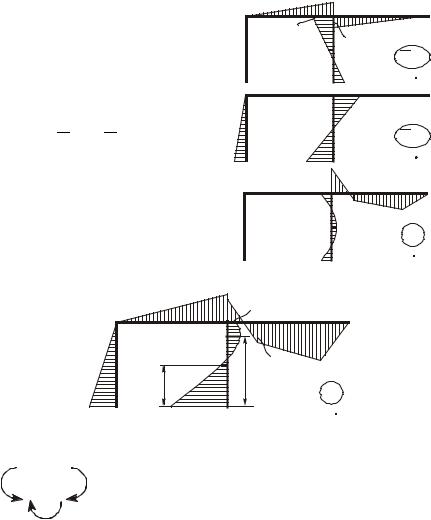
Вычисление единичных и грузовых реакций. В соответствии с типами реакций определяем их двумя способами: моментные реакции вырезанием узла, силовые – отсечением рамы от опор.
Яровая А. В. |
www.mechanika.org.ru |

4 |
Пример расчета рамы методом перемещений |
Определение моментных реакций. Найдем реакции r11B ,B r12B ,B
R1B pB 1-ой введенной связи от перемещений Z1B B = 1, Z2B B = 1 и от внешней нагрузки. Для этого вырежем жесткий узел с рассматриваемой связью в различных состояниях (рисунок 8) и рас-
смотрим его равновесие. Каждый раз будем составлять уравнение ∑ÌP óçëàP = 0 и выражать из него искомую реакцию.
Связь 1 |
|
r11 |
|
|
|
|
|
|
Связь 1 |
|
|
r12 |
Связь 1 |
R1ð |
|
|
||||||||||||||||
Состояние |
|
|
|
|
|
|
Состояние |
|
|
Состояние |
|
|
||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
3EJ |
|
2 |
|
|
|
|
|
|
|
|
ð |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
3EJ |
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
P l |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qh2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
l |
|
|
|
|
|
|
4kEJ |
|
|
|
|
6kEJ |
|
32 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
h2 |
|
|
|
|
|
12 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 8 |
|
|
|
|
|
|
|
|
||||||||
r11B B = |
3EJ |
+ |
3EJ |
+ |
4kEJ |
= |
3EJ + |
|
3EJ |
+ |
4 0,7EJ |
= 2,30833 EJ |
; |
|||||||||||||||||||
|
|
3 |
||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
|
l |
|
|
|
αl |
|
|
|
h |
|
|
|
|
4 |
|
|
|
1,2 4 |
|
|
ì |
|
|
||||||||
r12B B = |
− 6kEJ |
= − |
6 0,7EJ |
= –0,46667 EJ |
; |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
h2 |
|
|
|
32 |
|
|
|
|
|
|
|
|
ì2 |
|
|
|
|
|
|
|
|
|||||||||
R1B ðB = |
|
qh2 |
|
− |
9 |
Pαl = |
13 32 |
− |
|
9 |
24 1,2 4 P = –22,65 êÍP P ì. |
|
|
|||||||||||||||||||
12 |
|
32 |
|
12 |
|
32 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
P P |
|
|
||
Определение силовых реакций. Найдем реакции r21B ,B r22B ,B R2B pB
2-й введенной связи от перемещений Z1B B = 1, Z2B B = 1 и от внешней нагрузки. Для этого отсечем раму от опор и рассмотрим ее равновесие в различных состояниях (рисунок 9). Будем составлять уравнение проекций на горизонтальную ось ∑ZP =P P 0P и выражать из него искомую реакцию.
r21B B = |
− |
6kEJ |
= − 6 0,7EJ = –0,46667 EJ |
; |
|
|
|||||||
|
|
|
h2 |
|
32 |
|
|
ì2 |
|
|
|
||
r22B B = |
3kEJ + 12kEJ |
= |
3 0,7EJ + |
12 0,7EJ |
= 0,38889 EJ |
; |
|||||||
|
|
h3 |
|
h3 |
qh |
33 |
13 3 |
33 |
|
ì3 |
|
||
. R2B ðB |
= |
|
qh |
|
− qh = − |
= − |
P = –19,50 êÍP P ì. |
|
|||||
2 |
|
2 |
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
P |
|
P P |
|
Проанализировав полученные значения, убеждаемся, что главные единичные реакции положительны, а для побочных выполняется условие взаимности r12B B = r21B .B
Яровая А. В. |
www.mechanika.org.ru |
Пример расчета рамы методом перемещений |
5 |
|||
|
|
Связь 2 |
|
|
r21 |
|
Состояние |
|
|
1 |
|
|
||
|
|
|
|
|
0 
 6kEJ
6kEJ 













 h2
h2
|
|
|
|
Связь 2 |
||
r22 |
|
|
Состояние |
|||
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3kEJ |
12kEJ |
|
|
h3 |
h3 |
|
|
|
Связь 2 |
|
|
R2p |
Состояние |
P |
P |
p |
|
|
q 

 0 qh/2
0 qh/2
Рисунок 9
Решение системы канонических уравнений. Подставим найденные значения единичных и грузовых реакций в систему канонических уравнений:
2,30833 EJ Z1B – 0,46667 EJ Z2B – 22,65 = 0;
–0,46667 EJ Z1B + 0,38889 EJ Z2B – 19,50 = 0. Решив систему, найдем неизвестные перемещения
|
1 |
2 |
|
|
1 |
3 |
|
Z1B B = 26,34 |
|
(êÍ · ìP |
); |
Z2B B = 81,75 |
|
(êÍ · ìP |
). |
EJ |
EJ |
||||||
|
|
|
P |
|
|
|
P |
Заметим, что Z1B B является углом поворота, Z2B B – горизонтальным перемещением.
Яровая А. В. |
www.mechanika.org.ru |
6 |
Пример расчета рамы методом перемещений |
Построение |
окончательной |
|
|
19,76 |
|
||||
эпюры изгибающих моментов. |
|
|
|
12,35 |
4,12 |
||||
Умножаем |
ординаты |
единич- |
|
24,58 |
|
|
|||
íûõ ýïþð íà |
найденные |
значе- |
|
16,46 |
|
||||
|
|
6,15 |
|
||||||
P |
|
P |
|
вычис- |
|
|
|
|
|
íèÿP перемещений ZB ,B P |
ZB ;B |
|
|
|
|
Ì1Z1 |
|||
|
1 |
|
2 |
эпюры |
|
|
|
|
|
ляем ординаты грузовой |
|
|
|
12,29 |
[êÍ ì] |
||||
в основной системе (рисунок 10). |
|
|
|
||||||
|
|
|
|
|
|||||
Ординаты |
окончательной |
|
|
|
38,15 |
|
|||
эпюры Ì находим по формуле: |
|
|
|
|
|
||||
M = M1Z1 +M2Z2 +Mp . |
|
|
|
|
Ì2Z2 |
||||
|
|
|
|
|
|||||
Эпюра изгибающих |
моментов |
|
19,08 |
|
38,15 |
[êÍ ì] |
|||
|
|
32,40 |
|
|
|||||
показана на рисунке 11. |
|
|
|
|
4,50 |
20,70 |
|||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
9,75 |
|
|
|
|
|
|
|
|
|
|
4,88 |
Ìp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9,75 |
|
[êÍ ì] |
|
|
|
|
19,76 |
|
|
Рисунок 10 |
|
|
|
|
|
|
15,94 |
|
|
|
||
|
|
|
|
|
|
3,82 |
|
|
|
|
|
|
|
5,37 |
|
|
|
|
|
|
|
|
|
1,27 |
ì |
16,85 |
24,82 |
|
|
|
|
|
|
|
|
||||
|
|
1,5ì |
|
2,51 |
|
|
|||
|
|
|
|
Ì |
|
|
|||
|
19,08 |
|
|
35,61 |
|
|
[êÍ |
ì] |
|
|
|
|
|
Рисунок 11 |
|
|
|
||
Проверка эпюры Ì. |
Ñ ò à ò è ÷ å ñ ê à ÿ ï ð î â å ð ê à . |
|||||
|
|
|
|
|
à) Проверка равновесия узлов. Вырезаем |
|
|
|
|
|
|
жесткий узел рамы (рисунок 12) и рассмат- |
|
|
|
|
|
|
риваем его равновесие, составляя уравнение |
|
19,76 |
|
|
|
óçëà |
|
|
15,94 |
ÌP |
P = 0: |
||||
|
|
3,82 |
|
|
19,76 – 15,94 – 3,82 = 0. |
|
|
|
Рисунок 12 |
Проверка выполняется. |
|||
á) Проверка ординат. Для участков, загруженных в пролете внешней нагрузкой, должны выполняться условия равенства сумм характерных ординат и их дополнений соответствующим балочным ординатам.
Яровая А. В. |
www.mechanika.org.ru |
Пример расчета рамы методом перемещений |
7 |
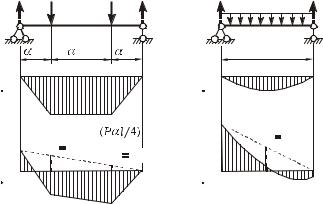
Выполняем проверку ординат. Для участков с двумя сосредоточенными силами и распределенной нагрузкой выбираем соответствующие балки (рисунок 13, à, á), имеющие тот же пролет и схему нагружения.
à) P |
P |
|
P P |
á) qh |
q |
qh |
|
|
|
|
|
|
2 |
|
2 |
|
l/4 |
l/2 |
|
l/4 |
|
h |
|
Ìá |
|
|
|
|
Ì á |
|
|
[êÍ ì] |
|
|
|
|
[êÍ ì] |
14,63(qh2/8) |
|
|
|
|
|
|
|
|
|
|
28,80 |
|
28,80 |
35,61 |
|
|
|
|
|
|
|
|
m3 15,90 |
|
|
15,94 |
m1 |
11,95 |
|
|
|
|
|
m2 |
3,98 |
|
|
|
|||
Ì |
|
|
Ì |
|
|
||
|
|
|
|
1,27 |
3,82 |
||
[êÍ ì] |
|
|
|
|
[êÍ ì] |
||
|
|
|
|
|
|||
|
16,85 |
|
24,82 |
|
|
|
|
Рисунок 13
Определив опорные реакции, строим балочные эпюры моментов ÌáP .P (Расчеты по построению ÌáP P не приводим из-за их простоты). Ниже изображаем эпюры изгибающих моментов для рассматриваемых участков, взятые из окончательной эпюры Ì (см. рисунок 11).
Соединяем крайние ординаты эпюр Ì прямыми линиями и находим из подобия треугольников дополнительные ординаты (на рисунке 13 они показаны пунктиром):
m1B B = |
3 |
15,94 = 11,95 êÍP ·P ì; m2B B = |
1 |
15,94 = 3,98 êÍP ·P ì; |
4 |
4 |
|||
|
|
P P |
|
P P |
m3B B = |
1 |
(35,61 − 3,82) = 15,90 êÍP ·P ì. |
|
|
2 |
|
|
||
|
|
P P |
|
|
Вычисляем суммы ординат эпюр Ì и соответствующих дополнений, сравниваем их с ординатами ÌáP .P Для первой эпюры
m1B B + 16,85 = 11,95 + 16,85 = 28,80 êÍP ·P P ì;P m2B B + 24,82 = 3,98 + 24,82 = 28,80 êÍP ·P P ìP .
Для второй эпюры
m3B B – 1,27 = 15,90 – 1,27 = 14,63 êÍP ·P P ìP .
Полученные значения совпадают с соответствующими характерными ординатами балочной эпюры моментов, проверка выполняется.
Яровая А. В. |
www.mechanika.org.ru |
8 Пример расчета рамы методом перемещений
Ä å ô î ð ì à ö è î í í à ÿ ï ð î â å ð ê à . Чтобы окончательно убедиться в правильности построения эпюры Ì, выполняем деформационную проверку. Она проводится так же, как и при расчете рам методом сил: вычисляется условное суммарное пе-
* |
|
|
|
|
|
ремещение ∆spB BP P перемножением окончательной эпюры Ì è ñóì- |
|||||
|
|
|
|
* |
|
марной единичной эпюры метода сил. Значение ∆spB BP P должно рав- |
|||||
няться нулю: |
|
|
|
|
|
|
l |
|
|
S* |
|
* |
MM |
||||
∆spB BP |
P = ∑∫ |
|
|
dz = 0, |
|
EJ |
|
||||
|
0 |
|
|
|
|
ãäå MS* – суммарная единичная эпюра изгибающих моментов, построенная для основной системы метода сил.
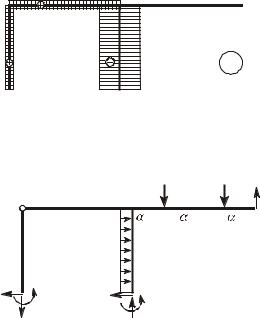
Вычисляем степень статической неопределимости заданной системы (см. рисунок 1) по формуле s = 3Ê – Ø = 3 · 2 – 3 = 3. Формируем основную систему метода сил, рассекая раму в шарнире и отбрасывая опорный стержень. Для компенсации отброшенных связей вводим три неизвестных усилия Õ1B ,B Õ2B ,B Õ3B .B
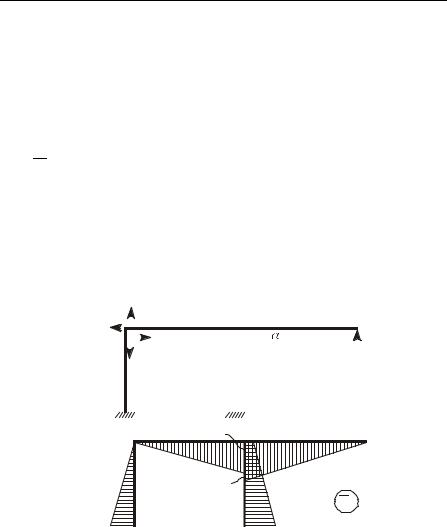
Далее рассматриваем суммарное воздействие на основную |
|||||||||||
систему единичных сиë Õ1B B = 1, Õ2B B = 1, Õ3B B = 1, Õ4B B = 1 (рисунок |
|||||||||||
14, à) и строим эпюру MS* |
(рисунок 14, б). |
|
|
||||||||
à) |
|
|
|
X2=1 |
l,EJ |
|
l, EJ |
|
|
||
|
|
|
|
|
|
||||||
|
|
|
|
|
X =1 |
|
|
|
|||
|
|
|
|
|
|
X =1 |
|
||||
|
|
|
|
|
|
|
|||||
|
|
1 |
EJ |
|
|
3 |
|
||||
|
EJ |
|
Основная |
||||||||
|
,hk |
,hk |
|
||||||||
|
система |
|
|||||||||
|
|
|
|
|
|
|
|
|
метода сил |
|
|
á) |
4,0 |
0,8 |
|
|
|
|
1,2 |
|
4,8 |
3,6 |
|
|
2,3 |
|
|
|
|
Ìs* |
|
|
|
|
|
3,0 |
|
3,8 |
[ì] |
Рисунок 14
Вычисляем ∆spB *PB :P
|
* |
|
|
|
h |
2 19,08 3 + |
l |
(−2 19,76 4) + |
|
∆spB PB P |
= |
|
|
|
|||||
6kEJ |
6EJ |
||||||||
+ |
|
h |
|
|
(−35,61 3,8 + 3,82 0,8 − 4 1,27 2,3) + |
||||
6kEJ |
|||||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
Яровая А. В. |
|
|
|
www.mechanika.org.ru |
|||||
|
|
|
|
Пример расчета рамы методом перемещений |
9 |
||||
+ |
|
αl |
(−2 15,94 4,8 + 2 16,85 3,6 −15,94 3,6 +16,85 4,8) + |
||||||
4 |
6EJ |
||||||||
|
|
|
|
|
|
||||
+ |
|
αl |
|
(2 16,85 3,6 + 2 24,82 1,2 +16,85 1,2 + 24,82 3,6) + |
|||||
2 |
6EJ |
||||||||
|
|
|
|
|
|
||||
+ |
|
αl |
2 24,82 1,2 = |
1 |
|
(209,869 −209,847) = |
0,022 . |
||
4 |
6EJ |
EJ |
|
||||||
|
|
|
|
EJ |
|||||
|
|
|
|
|
* |
близка к нулю, т. е. деформацион- |
|||
Полученная величина ∆spB BP P |
|||||||||
ная проверка выполняется. Следовательно, окончательная эпюра изгибающих моментов построена верно.
Замечание. Вместо деформационной можно выполнить универсальную проверку:
∑∫l MEJMS dz = –(R1B pB + R2B p),B
0
ãäå MS – суммарная единичная эпюра изгибающèõ моментîâ в основной системе метода перемещений: MS = M1 +M2 .
Построение |
эпюры |
|
|
27,32 |
|
||||
|
|
|
|
||||||
поперечных |
ñèë |
Q. |
|
|
3,32 |
|
|||
Эпюра |
|
поперечных |
|
|
|
||||
|
|
|
6,36 |
|
|||||
сил (рисунок |
|
15) |
ïî- |
|
4,94 |
|
|||
|
|
|
|
||||||
строена |
|
ïî |
|
готовой |
|
|
20,68 |
|
|
эпюре |
моментов. Ход |
|
|
|
|||||
|
|
ì |
|
||||||
расчета |
ничем |
íå |
îò- |
|
|
2,51 |
Q |
||
личается |
îò |
рассмот- |
|
|
|
||||
6,36 |
32,64 |
|
[êÍ] |
||||||
ренного |
ранее |
ïî |
ìå- |
|
|||||
|
|
||||||||
òîäó ñèë. |
|
|
|
|
|
Рисунок 15 |
|
||
|
|
|
|
|
|
|
|
|
|
Построение эпюры продольных сил N.
Эпюру N строим по готовой эпюре Q, рассматривая равновесие узлов рамы (рисунок 16). По полученным данным строим эпюру N (рисунок 17).
à) |
|
á) |
|
|
Óçåë Â 4,94 |
|
Óçåë K |
NK-C =0 |
|
|
|
NÂ-K |
|
|
6,36 |
NÂ-K |
|
27,32 |
|
4,94 |
|
|||
|
|
|||
|
|
6,36 |
|
|
|
NÀ-Â |
|
|
|
|
|
ND-K |
|
|
|
|
|
|
|
Рисунок 16
Яровая А. В. |
www.mechanika.org.ru |
10 |
Пример расчета рамы методом перемещений |
6,36
|
|
N |
4,94 |
32,26 |
[êÍ] |
Рисунок 17
Статическая проверка равновесия рамы. Отсечем раму от опор, в местах полученных сечений приложим внутренние силы и моменты, взятые из эпюр Ì, Q, N (рисунок 18).
|
|
|
|
P |
P |
20,68 |
|
B |
l |
|
l/4 |
l/2 |
l/4 |
h |
|
|
q |
h |
|
|
6,36 |
19,08 |
32,64 |
|
35,61 |
|
|
|
|
|
|
4,94 32,26
Рисунок 18
Составим уравнения равновесия рамы:
∑Z = 0 ; –6,36 – 32,64 + qh = –39 + 13 · 3 = 0;
∑Y = 0 ; –4,94 + 32,26 + 20,68 – 2P = 48 – 2 · 24 = 0;
∑MÂ = 0 ; 19,08 + 35,61 + 20,68(l + αl) + qh2P /2P + 32,26l –
–6,36h – 32,64h– P(l + αl/4) – P(l + 3αl/4) = = 54,69 + 20,68(4 + 4,8) + 13 · 32P /2P + 32,26 · 4 –
–6,36 · 3 – 32,64 · 3 – 24(4 + 1,2) – 24(4 + 3,6) =
= 424,214 – 424,2 = 0,014 êÍP ·P P ìP .
Точность подсчетов приемлемая. Рама находится в равновесии, значит, расчет выполнен верно.
Яровая А. В. |
www.mechanika.org.ru |
