Добавил:

neus500 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский авиационный институт (национальный исследовательский университет)

Предмет:

Высшая математика

Файл:

Лекции по Матанализу ч1

.pdf

Скачиваний:

418

Добавлен:

24.07.2017

Размер:

1.89 Mб

Скачать

☆

1 / 51 2 3 4 5 > Следующая >>>

К У Р С МАТЕМАТИЧЕСКОГО АНАЛИЗА

Часть 1

Оглавление
Оглавление..........................................................................................................................................	2
Введение в курс математического анализа......................................................................................	3
Понятие о логической символике.................................................................................................	3
Основные понятия о множествах .................................................................................................	3
Простейшие операции над множествами. ..................................................................................	4
Числовые множества. Числовая прямая. .....................................................................................	6
Основные числовые множества на действительной оси ...........................................................	7
Принцип математической индукции ............................................................................................	8
Неравенство Якоби Бернулли .......................................................................................................	9
Неравенство Коши .........................................................................................................................	9
Бином Ньютона. ...........................................................................................................................	10
Абсолютная величина числа (модуль числа) ............................................................................	11
Теорема о существовании целой части числа. .........................................................................	12
Верхняя и нижняя грани числовых множеств...........................................................................	13
Лемма о вложенных отрезках .....................................................................................................	14
Метрические и арифметические пространства. ........................................................................	14
Открытые, замкнутые и компактные множества ......................................................................	15
Определение функции .................................................................................................................	17
Способы задания функций ..........................................................................................................	19
Теория пределов функции одной переменной. .............................................................................	21
Предел числовой последовательности. ......................................................................................	21
Ограниченные и неограниченные последовательности. ..........................................................	21
Монотонные последовательности. .............................................................................................	22
Число е...........................................................................................................................................	23
Предел функции в точке. .............................................................................................................	25
Предел функции при стремлении аргумента к бесконечности. ..............................................	26
Бесконечно малые функции. .......................................................................................................	27
Основные теоремы о пределах....................................................................................................	28
Некоторые замечательные пределы. ..........................................................................................	28
Бесконечно большие функции и их связь с бесконечно малыми............................................	30
Сравнение бесконечно малых функций. ....................................................................................	31
Свойства эквивалентных бесконечно малых.............................................................................	32
Основные эквивалентности.........................................................................................................	32
Примеры........................................................................................................................................	33
Непрерывность функции в точке................................................................................................	35
Непрерывность некоторых элементарных функций.................................................................	36
Точки разрыва и их классификация. ..........................................................................................	37
Асимптоты. ...................................................................................................................................	40
Свойства функций, непрерывных на отрезке. ...........................................................................	43
Сложная функция .........................................................................................................................	44
Обратная функция........................................................................................................................	45

Введение в курс математического анализа

Понятие о логической символике

На ряду со специальными символами и терминами, которые будут вводиться в курсе математического анализа, рассмотрим распространенные символы математической логики.

- знак отрицания; знак A означает «не А» (отрицание высказывания А);

- знак конъюнкции, заменяет союз «и»;

- знак дизъюнкции, заменяет союз «или»; запись A B означает, что имеет место

хотя бы одно из высказываний А, В;- знак следования (импликация);

- знак равносильности (эквивалентности).

Данные символы записаны в порядке приоритета.

Взаписи высказываний о множествах часто используют логические операторы:

- знак (квантор) существования. Заменяет слова: «для любого», «для каждого», «для всех». Заметим, что - перевернутая буква английского слова All (все).

: - «такой что».

- знак (квантор) существования. Заменяет слова: «существует», «найдется».- перевернутая первая буква английского слова Exists (существует).

Примеры.

Пусть и некоторые высказывания, тогда:

1. - имеет место высказывание и одновременно.

2.- имеет место высказывание или .

3.x - для любого x имеет место высказывание .

4.x - существует x , для которого имеет место высказывание .

5.запись - означает, что влечет или следует из . Иначе: - необходимое условие (признак) , - достаточное условие (признак) .

6.Запись - означает, что следует из и следует из . Иначе:

равносильно ;	необходимо и достаточно для ; тогда и только тогда, когда .
def	Def :	является определением понятия .
7. (или ) – утверждение

Значок def означает, что сформулированное утверждение справедливо по определению (от английского definition – определение).

Аналогичное обозначение :

Основные понятия о множествах

Наиболее универсальным языком математики стал язык теории множеств. Основатель теории множеств немецкий математик Георг Кант (1845-1918гг).

Множество элементов (объектов) - одно из первичных (неопределенных) понятий математики, является одним из самых фундаментальных в математике.

Синонимы: множество, совокупность, собрание, коллекция объектов, объединяемых по какому-то правилу, характеристическому свойству).

Вообще, всеобъемлющего определения множества не существует.

Множества обозначаются заглавными буквами A, B, C,…. Объекты множеств назовем его элементами и будем обозначать маленькими буквами: a, b, c,…

Множества определяются некоторым свойством а, которым должен обладать или не обладать каждый из рассматриваемых объектов: те объекты, которые обладают свойством а, образуют множество А.

Будем в дальнейшем рассматривать множества, входящие в некоторое определенное «универсальное» множество объектов М. Тогда множества объектов A, B, C,… и т.д.

некоторые подмножества из М. Если а – элемент множества А, то пишут a A ( а принадлежит множеству А) или A a (множество А содержит элемент а).

Факт непринадлежности элемента «а» множеству А обозначается так a A (т.е. не обладает свойством а).

Частные случаи множеств:

конечное – состоящее из конечного числа элементов;

бесконечное – состоящее из бесконечного числа элементов;

- пустое множество. Множество, не содержащее ни одного элемента. Два множества называются равными, если состоят из одних и тех же элементов:

def
( A B) ( A B) (B A)
Отрицание равенства	A B .
Отношение между множествами A B называется отношением включения.
Запись A B(B A)	означает: любой элемент множества А является элементом

множества В.

или: А – является подмножеством множества В. или: В содержит А.

или: В включает А.

def

Итак, ( A B) x A, x B

(A B) : x M /(x A) (x B)

или

A B

Очевидно, что для любого множества А А.

Замечание: Если x – объект, Р – свойство, а Р(х)- обозначение того, что х обладает свойством Р, то через x / P(x) - обозначают класс объектов, обладающих свойством Р.

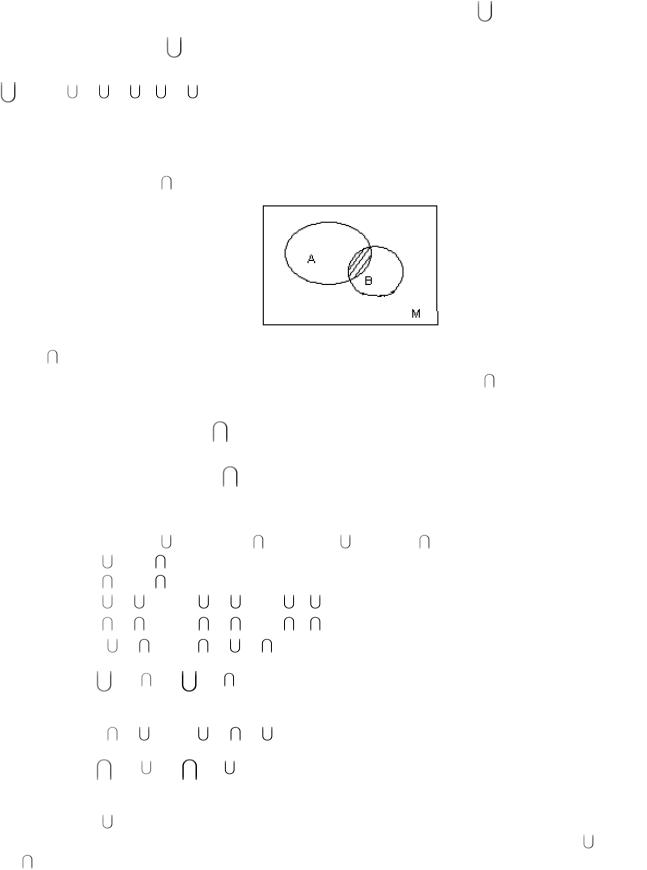
Простейшие операции над множествами.

Пусть A и B - подмножества множества М, т.е. A M и B M .

Определение 1. Объединением (соединением, суммой) множеств A и B называется множество, состоящее из все тех и только тех элементов М, которые содержатся хотя бы в

одном из множеств A или B .

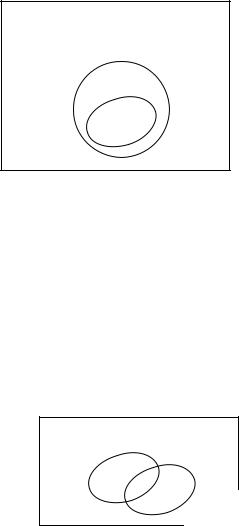
Обозначают: A B C x M / x A x B

Пример. 1, 2,3 1,3, 4,5 1, 2,3, 4,5

A B C

В A

	Обобщение. Если A - совокупность множеств A				из М, то	A есть объединение

всех	A	так,	что	A x M / x A ,хотя бы для одного ,		бесконечный набор

	A1			An ... x M / x A1 x A2 ,..., x An ...
An	A1	A2	A3 ...	An ... x M / x A1 x A2 ,..., x An ...
n 1
	Определение 2.			Пересечением (произведением)	множеств	A B называется

множество, образованное всеми теми элементами и только теми элементами множества М, которые принадлежат одновременно множествам A B .

Обозначение. A B C : x M /(x A) (x B) .

Пример.

1, 2,3

1,3, 4 1,3 .

Замечание. Если у множеств A B нет общих элементов, то A B .

Обобщение. Если A - совокупность множеств из М, то

A x M / x A при каждом .

x M / x An для любого n N .

Если бесконечный набор

n 1

Непосредственно из Df 1 2 следующие предположения:

A A , A

объед

пересеч.

A A, A

A A , A A, A

B B

A (коммутативность объединение);

B B

A (коммутативность пересечения);

C) (A B)

C A

C (ассоциативность объединения);

C) (A B)

C A

C (ассоциативность пересечения);

C (A

C) и вообще

( A

(дистрибутивность

пересечения

относительно

объединения);

C (A

C) и вообще

( A

(дистрибутивность

объединения

относительно

пересечения)

10.A M M (вытекает из Определения)

11. Отношение A B эквивалентно каждому из двух отношений

A B B ,

AB A

12.A B, B C , то A C свойство транзитивности вытекает непосредственно из

Определение.

13.A B, B A , то A B

Определение 3. Разностью между A B называется множество, состоящее из всех тех элементов множества А, которые не содержаться в множестве В.

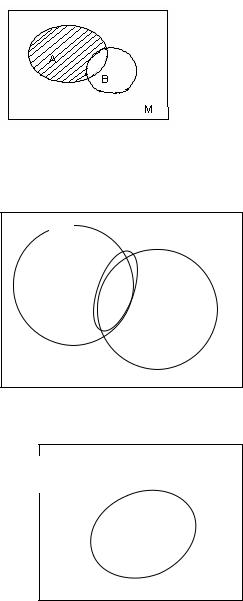
Обозначение: A \ B : x M / x A x B .

Пример. 1,2,3,4,5 \ 2,4,7,8,9 1,3,5

Пример. Пусть M N и A 1,2,3 , B 1,2,3,4,5 ,тогда A \ B 1 , B \ A 4,5 .

A \ B
A \ B			В
	A B



		B \ A


A B
A B				М
				М

Определение 4. Разностью между множеством М и содержащемся в нем подмножеством А обычно называют дополнением А в М и обозначают через CM A или CA

CM A

Числовые множества. Числовая прямая.

Понятие числа является первичным и основным в математике. Рассмотрим основные числовые множества.

Определение 1. Множество X называется индуктивным, если с каждым x X число

x 1 так же принадлежит X .
Если 1 R, 1 1 2 R, 2 1 3 R,...,(n 1) 1 n R,(n 1) R	Определённое
таким образом множество называется множеством натуральных чисел.
1. N 1,2,..., n, n 1 - множество натуральных чисел.
Аксиома (Принцип минимального числа). В любом непустом подмножестве
натуральных чисел (N ) существует минимальное число.
(Скажем, что p N является минимальным для множества A N ,	если p A и

p m, m A). Принцип минимума является одной из аксиом теории натуральных чисел. p

-минимальный элемент множества A ( p min A) .

2.Z ... (n 1),n,..., 1,0,1,2,..., n, (n 1),... - множество целых чисел.

	m			kp	p	, k Z, k 0

3.	Q	m Z , n N	и				, такое множество называется
				kq	q
	n

множеством рациональных чисел.

4.Иррациональными числами называется число, которое может быть представлено в виде бесконечной непериодической десятичной дроби.

5.– множество действительных (вещественных) чисел есть объединение

множеств рациональных и иррациональных чисел.

Аксиома полноты . Для любых 2-х непустых множеств действительных чисел X

и Y обладающих свойством, что	каждый элемент х Х , не превосходит каждого
элемента y Y , такое действительное с			с R , что неравенство х с y справедливо
для всех х Х и y Y .
X ,Y , x X и y Y, x y с : x c y
X				Y

X		C		Y

6. С x iy x , y , i2 1 – множество комплексных чисел. Тогда

N Z Q C

Действительные числа принято изображать точками прямой оси, на которой выбраны единица измерения отрезков, начальная точка и положительное направление между точками числовой оси и числами существует взаимно однозначное соответствие.

Основные числовые множества на действительной оси

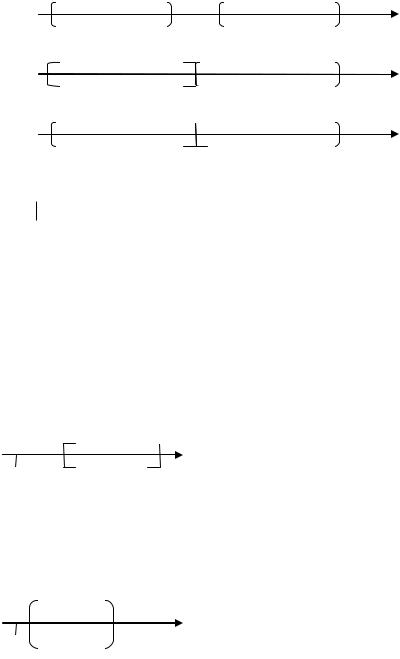
Определение 1. x R / a x b - называется отрезком a,b R и обозначается

a,b .

		a			b
0
- содержит свой минимальный - min( ) a и свой максимальный -									max( ) b
элементы.		J x R / a x b -
Определение	2.	J x R / a x b -				называется	интервалом	a,b R и
обозначается J (a,b)
	a		J	b
			J
0
J - не имеет минимального и максимального элементов.
Определение	3.			K1 {x R / a x b},		K2 {x R / a x b} -			называются
полуинтервалами для a,b R и обозначаются K1						(a,b], K2	[a,b) .

- имеет max( k1 ) b , не имеет min(k1 ) .

K1 b

- имеет min(k2 ) a , не имеет max( k2 ) .

Определение 4. Интервалы, отрезки и полуинтервалы называются числовыми

промежутками, или просто промежутками.

Эти промежутки есть ограниченные множества.

В математике рассматриваются также бесконечные промежутки, употребляя в их

записи символы: , , при этом x R справедливо неравенство: x

По определению:

a : x R / x a

[a ) : x R / x a

Оба эти промежутка не ограниченны сверху.

, b : x R / x b ,

( , b] : x R / x b

Оба эти промежутка не ограниченны снизу.

Определение 5. Любой интервал J, который содержит фиксированную точку x0 R

называется окрестностью этой точки.

J x R / x0 x x0

x0 x0

называется

- окрестностью точки

причем 0

при этом также

справедлива запись: J x R / | x x0 | . Обозначение J x0 ;

J (x0 , )

Принцип математической индукции

Теорема.

Пусть

некоторое множество

натуральных

чисел ( A N)

удовлетворяет следующим 2-м условиям:

1.1 A .

2.если n A , то (n 1) A ,

тогда множество А содержит все натуральные числа, т.е. A N .

	Доказательство: Допустим, что утверждение теоремы не имеет места, т.е. A N .
	CA CN A N \ A . Тогда		CA A и A . В силу принципа минимума
p0	CA такое, что m CA m p0 , p0 A .
	В силу условия 1) p0	1, но тогда ( p0 1) N и, кроме того, поскольку ( p0 1) CA ,
то	( p0 1) A . Но тогда	в силу	условия 2) ( p0 1) 1 p0 A, что противоречит

отношению p0 A .

Итак, CA , т.е. A N (так как ( p0 1) p0 , где p0 CA ).

На основании этой теоремы формулируется метод, который очень удобно использовать при доказательстве некоторых теорем.

Метод математической индукции. Чтобы доказать, что некоторое утверждение A n справедливо для любого (n N ) , достаточно доказать, что:

1)это утверждение справедливо при n 1

2)Из справедливости утверждения при n k следует справедливость утверждения

при n k 1

Пример. Докажем, что n N имеет место равенство

k 2

n(n 1)(2n 1) .

k 1

Пусть A n N /

k 2

n(n 1)(2n 1) .

k 1

Заметим, что при n=1 12

1 (1 1)(2 1 1) 1, т.е. 1 A .

Далее, если n A , то

(n 1) 2n2

n 6n 6

k 2 (n 1)2

n(n 1)(2n 1) (n 1)2

k 1

(n 1) (n 1) 1 2(n 1) 1

n 1

(n 1)(n 2)(2n 3)

k 2

k 1

откуда следует, что

(n 1) A .

В силу принципа математической индукции имеем

A N , т.е. наша формула справедлива

n N .

Неравенство Якоби Бернулли

(1654-1705 г.г, швейцарский математик)

Теорема. Для R, 1 и n N справедливо неравенство

	(1 )n 1 n	(1)
Доказательство. Применим метод математической индукции
1.	1 A , т.к. (1 )1 1 - очевидно.
2.	Пусть n A , тогда ( 1)n 1 (1 )n (1 ) (1 n )(1 ) , (1 ) 0 .

1 (n 1) n 2 1 (1 n) , (т.к. n 2 0 ), (n 1) A . Согласно принципу математической индукции A N . Наше утверждение доказано.

Неравенство Коши

Среднее геометрическое нескольких положительных чисел не больше их среднего

арифметического.
Теорема. (неравенство Коши) Для любого набора a1 , a2 ,...an 0, справедливо
неравенство
					a1 a2 ... an	, n N , (1)
n a a	2	... a		n	a1 a2 ... an
n a a		... a
1					n
					n
Причем знак равенства возможен , когда a1 a2 ... an .
Доказательство: Прежде всего,			отметим, что если хотя бы одно из ai 0 . Тогда

левая часть неравенства (1) равна нулю, а правая неотрицательна, т.е. неравенство Коши выполняется. Поэтому будем далее предполагать, что все ai 0 . Докажем вначале вспомогательное неравенство. Обозначим

k a

Тогда

k 1

В соответствии с неравенством Бернулли имеем

k 1

1 k

Таким образом

k 1 Gk 1

ak 1

kGk

(2)

k 11

1 Gk 1 kGk

Воспользуемся теперь методом математической индукции

a1 a2

1) При n 2

(1) принимает вид

a a

, что легко доказать, исходя из

)2 0 .

неравенства ( a

2) Предположим, что (1) справедливо при n k . Докажем, что оно справедливо и

при n k 1. Имеем по предположению индукции

a a

... a

k k a a

... a

k 1 Gk 1

a1 a2 ... ak

ak 1 kGk

kGk

Последнее неравенство означает, что

a1 a2

... ak 1

k 1 a a

... a

k 1

Неравенство Коши доказано.

Бином Ньютона.

а, в

n N справедливо разложение

a b n an

nan 1 b

n n 1

an 2 b2 ...

n n 1 ... n k 1

an k bk ... n a bn 1 bn . (*)

1 2

1 2 3... k

Обозначения.

1) 1 2 3... n n! причем 0! 1, 1!

n n 1 ... n k 1

C k ; или Сk

;

1, C n

1 2

3 ... k

k! n k !

Cnk - число сочетаний из “n” по “k”

С – первая буква французского слова combination – сочетание.

Тогда

(a b)n C0an C1an 1b C2an 2b2

... Ck an kbk

... Cn 1abn 1 Cnbn

Ck an kbk

k 0

Где Cnk an k bk - называют членами разложения (*), а числа Cnk

- коэффициентами

разложения или биноминальными коэффициентами.

n N /(a b)n

Ck an kbk . Тогда для этих чисел

Доказательство: Пусть A

k 0

выполняется формула бинома Ньютона. Проверим это с помощью метода математической индукции

1 / 51 2 3 4 5 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
24.07.201785.64 Кб20Вопросы для студентов вечернего отделения от кафедры 311.pdf
#
24.07.20171.19 Mб151Лекции по Матанализу ч.3.pdf
#
24.07.20171.89 Mб418Лекции по Матанализу ч1.pdf
#
24.07.20171.2 Mб158Лекции по Матанализу ч2.pdf
#
24.07.2017166.23 Кб112Матанализ Вопросы 1 курс 1 семестр.pdf
#
24.07.2017129.01 Кб46Некоторые задачи для вечернего отделения третьего факультета от каф 311.pdf