
- •Расчет основных геометрических параметров самолета. Расчет геометрических параметров фюзеляжа.
- •Расчет геометрических параметров несущей поверхности (крыла, горизонтального, вертикального оперения)
- •Определение критического числа Маха.
- •Расчет аэродинамических характеристик самолета и его частей в продольной плоскости при малых углах атаки.
- •Определение коэффициента подъемной силы самолета.
- •Определение производной коэффициента подъемной силы фюзеляжа по углу атаки.
- •Определение коэффициента момента тангажа и фокуса по углу атаки самолета.
- •Определение коэффициента лобового сопротивления самолета.
- •Построение поляры первого рода, зависимости для самолета приили
- •Коэффициент подъемной силы крыла при отклонении управляющих поверхностей (,)
- •Построение балансировочной поляры самолета нормальной аэродинамической компоновки при .
- •Расчет аэродинамических характеристик самолета в боковом установившемся движении.
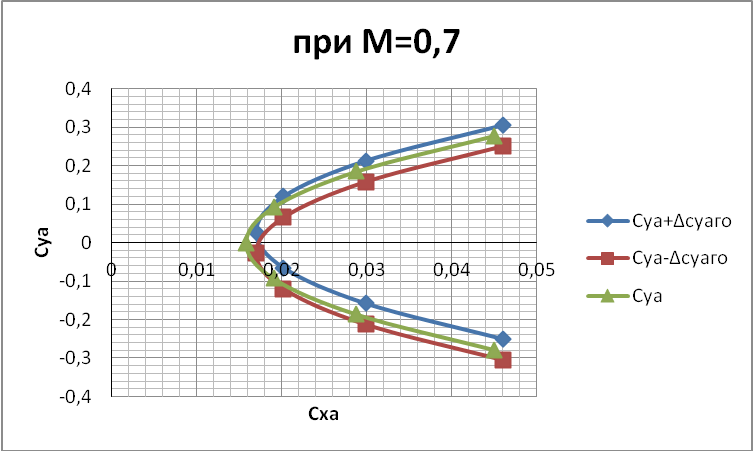
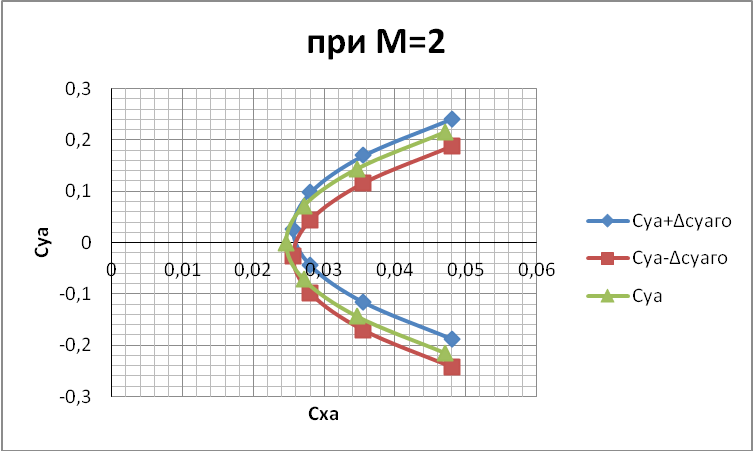
Построение балансировочной поляры самолета нормальной аэродинамической компоновки при .
1)
По оси
![]() откладывается
от т.О
откладывается
от т.О
![]() или
или![]() .
.
2)
По оси
![]() от точки
от точки
![]() откладывается
значение
откладывается
значение
![]() при
при
![]() ,
точки О"
и О'
,
точки О"
и О'
3)
Построение поляр самолета 2 и 3 при
отклонении горизонтального оперения
на балансировке: смещение исходной
поляры 1 таким образом, чтобы т.
О
совпала с т. О
- поляра 2 и с т. О"
-
поляра 3, На полярах 3 и 2 точки А и В,
соответствующие
![]() самолета
при
самолета
при
![]() .
.
4)
Точки АОВ
соединяются. Полученная кривая -
балансировочная поляра. В т. О,
О,
О"
касательные к этим полярам перпендикулярны
оси
![]() .
Отвал балансировочной поляры
.
Отвал балансировочной поляры![]() ,
больше отвала исходной поляры1,
что определяет потери на балансировку.
,
больше отвала исходной поляры1,
что определяет потери на балансировку.
Балансировочная поляра самолета

Расчет аэродинамических характеристик самолета в боковом установившемся движении.
Определение коэффициентов поперечной силы и моментов крена и рыскания самолета.
При наличии угла скольжения самолета возникают поперечная сила (Z) и аэродинамические моменты крена ( Мх ) и рыскания ( My ), которые выражаются через аэродинамические коэффициенты:
![]() ,
,
![]() ,
,![]()
При малых углах атаки и скольжения:
![]() ,
,
![]() ,
,![]()
Тогда основными аэродинамическими характеристиками самолета в установившемся боковом движении можно считать следующие зависимости:
![]() ,
,
![]() ,
,![]()
При
определении
![]() ,
,![]() рассматриваетсяисходный,
а не эквивалентный фюзеляж
рассматриваетсяисходный,
а не эквивалентный фюзеляж
Определение коэффициента поперечной силы самолета.
Аэродинамическую
поперечную силу самолета определяют,
в основном, поперечные силы, возникающие
при обтекании фюзеляжа -
![]() ,
вертикального
оперения (ВО) -
,
вертикального
оперения (ВО) -
![]() ,
мотогондол (МГ) -
,
мотогондол (МГ) -![]() ,
и
поперечная сила, вызванная интерференцией
между фюзеляжем и вертикальным оперением,
между плоскостями вертикального
оперения, состоящего из двух килей.
Поперечная сила от несимметричного
обтекания правой и левой части консолей
крыла и горизонтального оперения в
данном случае мала и ею можно пренебречь.
,
и
поперечная сила, вызванная интерференцией
между фюзеляжем и вертикальным оперением,
между плоскостями вертикального
оперения, состоящего из двух килей.
Поперечная сила от несимметричного
обтекания правой и левой части консолей
крыла и горизонтального оперения в
данном случае мала и ею можно пренебречь.
![]() ,
,
![]() ,
,![]()
где
![]() ,
,
![]() ,
,![]() -
производные коэффициентов поперечной
силы изолированного фюзеляжа, ВО с
учетом интерференции с фюзеляжем и
между плоскостями ВО (при двух килях),
изолированной мотогондолы,
-
производные коэффициентов поперечной
силы изолированного фюзеляжа, ВО с
учетом интерференции с фюзеляжем и
между плоскостями ВО (при двух килях),
изолированной мотогондолы,
![]() ,
,
![]() - коэффициенты торможения потока с
области вертикального оперения и
мотогондол, их значение можно принять
равным коэффициенту торможения ВО и МГ
при их обтекании c
- коэффициенты торможения потока с
области вертикального оперения и
мотогондол, их значение можно принять
равным коэффициенту торможения ВО и МГ
при их обтекании c
![]() ,
,
![]() ,
,![]() ,
,![]() ,площади
миделевого сечения фюзеляжа, ВО и
миделевого сечения МГ, соответственно.
,площади
миделевого сечения фюзеляжа, ВО и
миделевого сечения МГ, соответственно.
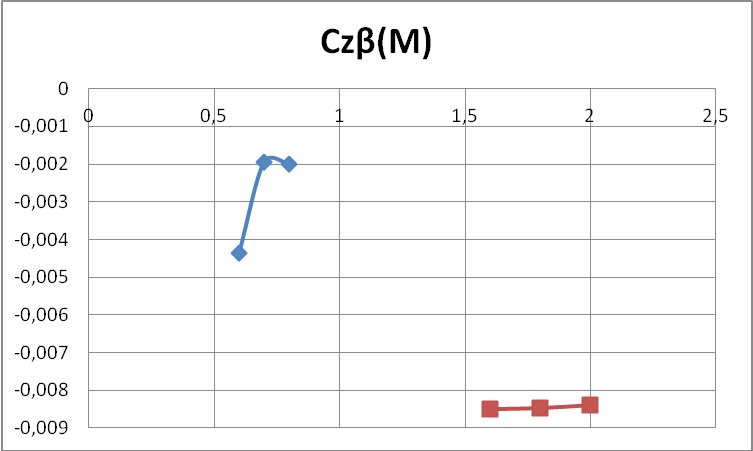
Производная коэффициента поперечной силы по углу скольжения самолета:
![]()
где
![]() ,
,
![]() ,
,![]() -производные
поперечной силы по углу скольжения
изолированных фюзеляжа и МГ, изолированного
ВО;
-производные
поперечной силы по углу скольжения
изолированных фюзеляжа и МГ, изолированного
ВО;
![]() -коэффициент,
учитывающий интерференцию между ВО и
фюзеляжем;
-коэффициент,
учитывающий интерференцию между ВО и
фюзеляжем;
![]() -
число килей;
-
число килей;![]() -
коэффициент эффективности затененной
плоскости
ВО.
-
коэффициент эффективности затененной
плоскости
ВО.
![]() ,
,
![]()
где
![]() -
производная
коэффициента подъемной силы несущей
поверхности, состоящей из двух консолей
ВО.
-
производная
коэффициента подъемной силы несущей
поверхности, состоящей из двух консолей
ВО.
![]() определяется
по графикам., где
определяется
по графикам., где
![]() средняя
относительная толщина профиля ВО по
его высоте,
средняя
относительная толщина профиля ВО по
его высоте,
![]()
![]() ,
,
![]()
![]() -
диаметр фюзеляжа в области ВО.
-
диаметр фюзеляжа в области ВО.
|
M∞ |
0,6 |
0,7 |
0,8 |
1,6 |
1,8 |
2 |
|
Cyaαво |
0,034594 |
0,038235501 |
0,040147276 |
0,041876977 |
0,034594 |
0,031863 |
|
Czβво |
0,017297 |
0,01911775 |
0,020073638 |
0,020938489 |
0,017297 |
0,015931 |
|
Kβ+ΔKβ |
0,7 |
0,7 |
0,7 |
1,312819843 |
1,206408 |
1,118562 |
|
Ктво |
0,995 |
0,995 |
0,995 |
0,963 |
0,95 |
0,93 |
|
Сzβ |
-0,00435 |
-0,00194 |
-0,00199 |
-0,00851 |
-0,00848 |
-0,00839 |
Определение коэффициента момента крена самолета.
Аэродинамический момент крена самолета Mx создается силами, действующими на крыло, горизонтальное и вертикальное оперения. Если = 0 или = 0 при отсутствии углов установки крыла и ГО, при неотклоненных рулях управления моментом крена, Mx будет создаваться силой, действующей на ВО при 0 и боковой силой, вызванной наличием поперечного "V" у крыла и ГО.
Согласно (7.1), (7.2) коэффициент момента крена самолета можно определить производной коэффициента момента крена по углу скольжения :
![]()
![]() -
производные
момента крена но углу скольжения самолета
от сил, вызванных "V"- образностью
крыла и ГО , действующих на ВО, от сил
интерференции ВО и фюзеляжа, соответственно.
-
производные
момента крена но углу скольжения самолета
от сил, вызванных "V"- образностью
крыла и ГО , действующих на ВО, от сил
интерференции ВО и фюзеляжа, соответственно.
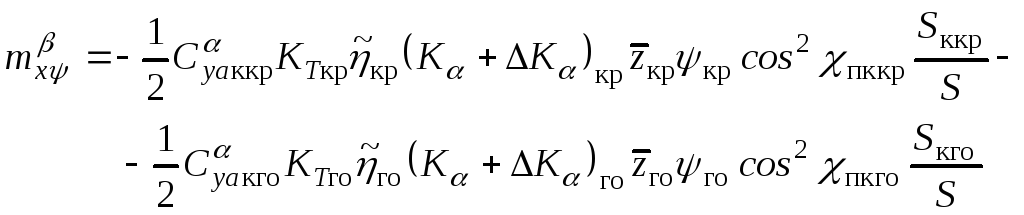
 ,
,![]() расстояние
до базовой плоскости самолета (плоскости
симметрии) от центра тяжести площади
консольной части крыла и ГО , соответствённо;
расстояние
до базовой плоскости самолета (плоскости
симметрии) от центра тяжести площади
консольной части крыла и ГО , соответствённо;
![]() угол"V"-
образности крыла и ГО, соответственно.
угол"V"-
образности крыла и ГО, соответственно.
![]() .
.
![]()
где
![]() - расстояние от продольной оси самолета
до центра тяжести площади ВО.
- расстояние от продольной оси самолета
до центра тяжести площади ВО.
![]() ,
,
где
-

![]() -
средняя высота фюзеляжа в сечении
плоскости симметрии в пределах центральной
хорды крыла и ГО, соответственно,
-
средняя высота фюзеляжа в сечении
плоскости симметрии в пределах центральной
хорды крыла и ГО, соответственно,
![]() ,
- центральная хорда крыла и ГО,
соответственно.
,
- центральная хорда крыла и ГО,
соответственно.
|
hфкр |
1,57 |
hфго |
1,31 |
|
|
|
|
кикр |
-0,12 |
киго |
-0,12 |
|
|
|
|
yво |
2,549 |
|
|
|
|
|
|
M∞ |
0,6 |
0,7 |
0,8 |
1,6 |
1,8 |
2 |
|
mβxи |
-0,00901 |
|
|
|
|
|
|
mβxво |
-0,00067 |
-0,0007465 |
-0,0007838 |
-0,0014841 |
-0,0011 |
-0,0009 |
|
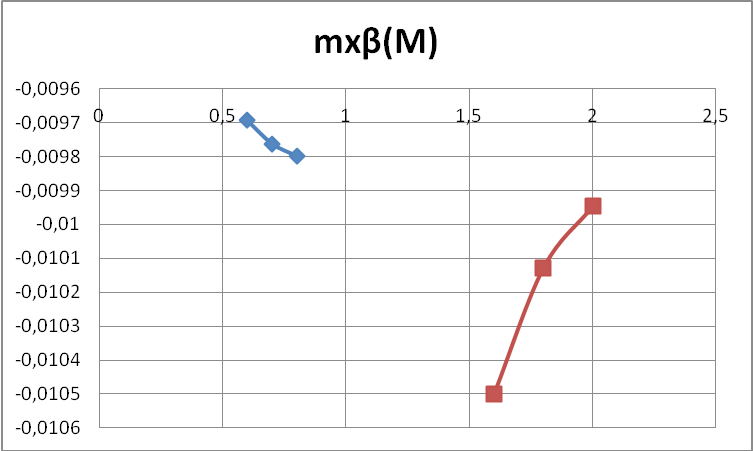
mβx |
-0,00969 |
-0,0097624 |
-0,009799 |
-0,0105000 |
-0,0101 |
-0,0099 |
Определение коэффициента момента рыскания самолета.
Аэродинамический момент рыскания самолета Му появляется при скольжении самолета ( 0) и при отклонении руля направления, элеронов и интерцепторов и создается поперечными и продольными силами действующими на ВО , фюзеляж, МГ, крыло и ГО (при = 0, 0 0).
При = 0 или = 0 и малом коэффициент момента рыскания самолета можно характеризовать производной коэффициента момента рыскания самолета по углу скольжения.
![]() ,
,
где
![]() -
производная коэффициента момента
рыскания по углу скольжения фюзеляжа
и ВО соответственно,
-
производная коэффициента момента
рыскания по углу скольжения фюзеляжа
и ВО соответственно,
![]() > 0
> 0![]() <
0.
<
0.
![]()
где
![]() -
расстояние от центра масс самолета до
фокуса по углу скольжения ВО (
-
расстояние от центра масс самолета до
фокуса по углу скольжения ВО (![]() ).
).
Координату
фокуса ВО по углу скольжения можно
определить как относительную координату
фокуса по углу атаки
![]() для несущей поверхности с относительными
геометрическими параметрами ВО.
для несущей поверхности с относительными
геометрическими параметрами ВО.
![]() ,
,
где
![]() ;
;![]()
![]() -
максимальная высота фюзеляжа в боковой
проекции,
-
максимальная высота фюзеляжа в боковой
проекции,
![]() -
длина фюзеляжа,
-
длина фюзеляжа,
![]() -
удлинение фюзеляжа
-
удлинение фюзеляжа
![]() -
расстояние от центра масс самолета до
носка фюзеляжа.
-
расстояние от центра масс самолета до
носка фюзеляжа.
Если положение центра масс неизвестно, то можно принимать за начало отсчета (начало координат системы ХYZ ) переднюю кромку САХ крыла с подфюзеляжной частью.
|
M∞ |
0,6 |
0,7 |
0,8 |
1,6 |
1,8 |
2 |
|
|
0,64 |
0,51 |
0,36 |
1,56 |
2,24 |
3 |
|
λво*Корень |
1,4565905 |
1,300267109 |
1,092442882 |
2,274101204 |
2,725031 |
3,153611 |
|
x`Fαво |
0,225 |
0,215 |
0,205 |
0,37 |
0,43 |
0,45 |
|
xFво |
0,71325 |
0,68155 |
0,64985 |
1,1729 |
1,3631 |
1,4265 |
|
Lво |
11,61325 |
11,58155 |
11,54985 |
12,0729 |
12,2631 |
12,3265 |
|
L'во |
10,9 |
|
|
|
|
|
|
myβво |
0,0030774 |
0,003392015 |
0,003551867 |
0,007029453 |
0,005347 |
0,004493 |
|
myβф |
2,2478224 |
2,232468869 |
2,210957298 |
1,784387539 |
1,65064 |
1,558833 |
|
х'ф |
6,6324404 |
6,587776562 |
6,52519886 |
5,284296695 |
4,89522 |
4,628152 |
|
кβ |
2,092471 |
2,078178603 |
2,058153738 |
1,661065046 |
1,536561 |
1,451099 |
|
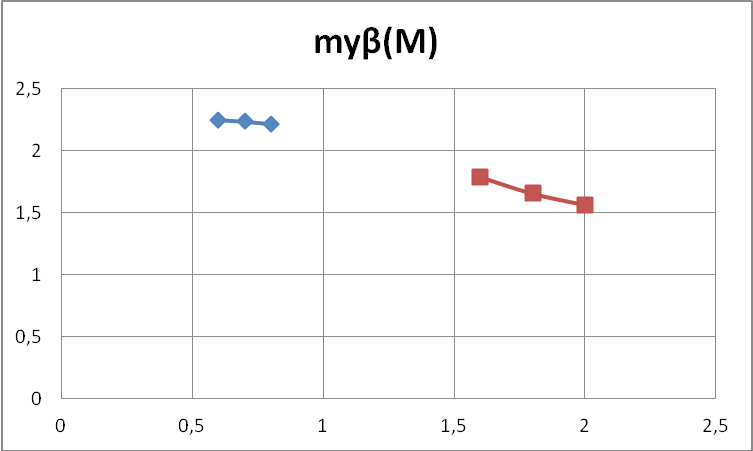
myβ |
2,2508998 |
2,235860884 |
2,214509165 |
1,791416992 |
1,655987 |
1,563326 |
Расчет координаты фокуса самолета по углу скольжения
Фокус
самолета по углу скольжения
![]() при малых углах
определяется соотношениями:
при малых углах
определяется соотношениями:

|
|
0,6 |
0,7 |
0,8 |
1,6 |
1,8 |
2 |
|
x`Fβ |
13,14289 |
29,18875 |
28,25772 |
5,34388 |
4,95884 |
4,73209 |
|
y`Fβ |
-0,05659 |
-0,12745 |
-0,12505 |
-0,03132 |
-0,03033 |
-0,0301 |
