2.2.2. Построение классификации для нормального распределения.

Классификация объекта для двух нормальных распределений с равными матрицами ковариации и разными математическими ожиданиями:

,

, матрица ковариации

где ковариация компонентi и j;

- дисперсия компоненты i

Матрица может быть определена следующим образом:

Если взять f(x) = const и выбрать const таким образом, чтобы она была маленькой, то

- определяет эллипсы в многомерном пространстве, дающие описание

многомерной плотности с помощью линий равной плотности вероятности.

Вопрос в том, как найти правильное C для многомерного случая?

Как строится правило решения для классификации двух классов?

Предполагается, что есть 2 класса.

,

где К- порог.

Решение строится на основе функции правдоподобия:

;

для удобства работы прологарифмируем:

Преобразовав выражение, получим правило в следующем виде:

- это уравнение линейной дискриминантной функции, полученной на основе Байесовского решающего правила.

Для дальнейшего анализа будем считать:

C (2/1) =C (1/2)

- простейшая дискриминантная функция

Пусть , размерность пространства возьмем равную 2 . Тогда получаем следующее правило решения

W – весовой вектор

Области классов представляют собой сферы. Положение этой плоскости определяется вектором W. Решающая плоскость перпендикулярна вектору

Уравнение решающей плоскости:

- это уравнение сферы можно свести к выражению

Утверждение:

Для данной решающей функции вектор лежит ровно на середине вектора

Таким образом, в случаях

a)

b)

решение выглядит следующим образом:

Рассмотрим случай, когда матрица не является единичной: нужно получить уравнение для решающей функции:

2.2.3.Числовые примеры

Вариант 1

Вариант 2

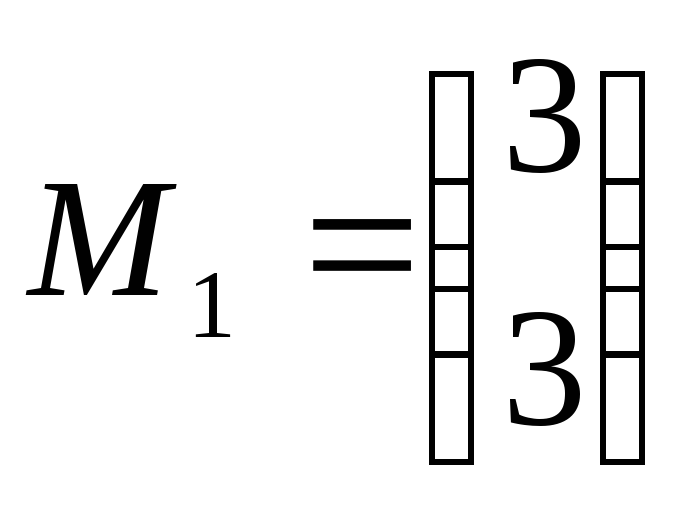
Решение варианта 1:

Решение варианта 2:

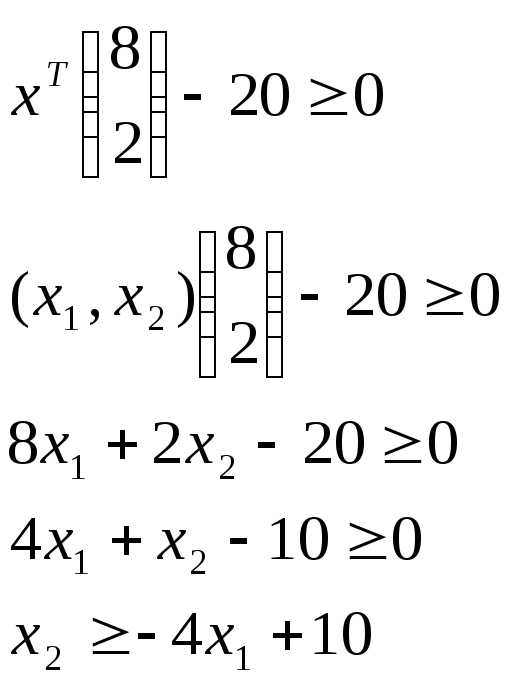
4

3

1

1 2 3 4

Найдем уравнение эллипса равной плотности вероятностей для варианта 2.

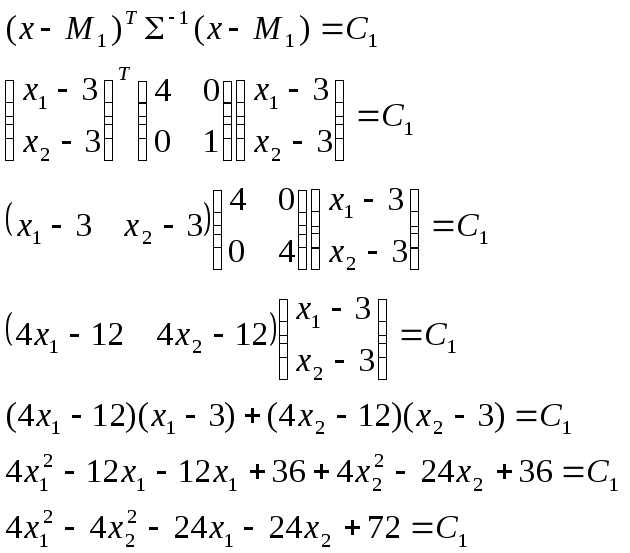
в общем виде:

соответственно полуоси:

2.2.4. Оценка качества классификации

Рассмотрим случайную величину , являющейся значением решающей функции. Решение принимается сравнением U с порогом

В исходной постановке задачи мы рассматривали многомерное пространство:

Так как решение принимается на основе одномерной величины U, то можно считать, что

задача классификации сводится к редукции пространства, то есть от n-мерного пространства мы переходим к пространству

Что мы имеем: в исходно пространстве условные плотности – многомерные нормальные распределения:

C

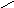
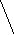
А в редуцированном пространстве переходим к одномерным условным нормальным распределения величины U.

то есть каждому многомерному распределению соответствует одномерное.

- это пороговое значение, то есть проблему принятия решения мы сводим к одномерной задаче. Ошибки классификации могут быть определены через распределения U.

(принимаем решение 1 при верности решения 2)

,

где C – порог

Прямое вычисление ошибок в многомерном пространстве приводит к техническим трудностям, поэтому и применяется редукция пространства.

Основная задача состоит в поиске распределений плотности вероятностей значений решающей функции .

в конечном итоге, это линейная комбинация нормально распределенных величин, она сама – нормальная величина. Найдем условные математические ожидании и дисперсии U по классам

, где

- расстояние Махаланобиса.

Аналогично мы должны посчитать :

Мы нашли математические ожидания ошибок.

Следующая задача состоит в нахождении дисперсий данной величины:

В предположении равенства матриц ковариации в исходном пространстве, получаем, что дисперсии U также равны по классам.

Здесь вывод достаточно длинный. Так как матрицы ковариации одинаковые, то можно сделать следующий вывод:

DU₁ = DU₂

M{(V - MV)²} = M{(V - MV)^T(V - MV)}

D = (M₁ - M₂)^Т^-1(M₁ - M₂) =  = ² ,

где  - расстояние Махаланобиса.

U может принадлежать двум нормальным распределениям:

U₁  N(, );

U₂  N(-, ).

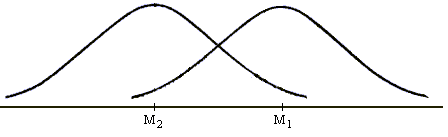
Эти распределения представлены на рисунке.

MU1 =  MU2 = - MU1 – MU2 = 

 - это не что иное, как обобщенное расстояние между классами в N-мерном пространстве.

 = (M₁ - M₂)^T ^-1(M₁-M₂)

Смысл этого расстояния довольно простой:

Если  = I, то

 = (M₁ - M₂)^T(M₁ - M₂) = (M₁ⁱ - M₂ⁱ)² = ║M₁ - M₂║² = d²

Если матрица диагональная, но с разными , то:

		12 0
 =		.
		0 n2
								2 - сумма взвешенных расстояний по каждой координате
 =				M1i - M2i
				i

 хорошо описывает статистическую природу данных.

 = X^T ^-1(M₁ - M₂) - (M₁ + M₂)^T ^-1(M₁ - M₂)

M{U/1} =   = (M₁ - M₂)^T ^-1(M₁ - M₂)

M{U/2} = -

D[U] = M[(U - MU)²] = M[(U - MU)^T(U - MU)]

D[U] = 

_n² = 

Нужно построить вероятности ошибок классификации.

U  C C = ln K K =	q2C(1|2)
	q1C(2|1)

N(, ) N(-, )

P = q₁ P(2|1) + q₂ P(1|2) - вероятность полной ошибки

P(2|1) = exp[]dU

f(U|1) = exp[]

P(2|1) = exp[]dU = dt =

= Ф()

P(1|2) = exp[]dU = dt =

= 1 - Ф(), где Ф(x) – интеграл ошибок Гаусса.

Полная ошибка распишется следующим образом:

P_ош = q₁ Ф() + q₂ [1 - Ф())]

Рассмотрим свойства полной ошибки:

C = ln K = ln = 0

q₁ = q₂ = 0.5

C(1|2) = C(2|1)

P_ош = 0.5 Ф() + 0.5 [1 - Ф()] =

= 0.5 [1 - Ф()] + 0.5 [1 - Ф()] = 1 - Ф()

Так как Ф(-х) = 1 – Ф(х).

Вернемся к рассмотрению :

Пусть

 = (M₁ - M₂)^T ^-1(M₁-M₂) =

Если _i² = 1, тогда  = (M₁ⁱ - M₂ⁱ)² = d²

Ошибка зависит от обобщенного расстояния d², чем больше d², тем меньше ошибка (так как расстояние между распределениями увеличивается).

M1i - M2i	= 	- это взвешенное нормальное распределение
i

Если  = const, тогда  будет представлять собой следующее:

 = ² = n ²

d = 

P_ош = 1 – Ф()

Пусть мы хотим сделать вероятность ошибки 0,005 = 0,5%.

P_ош = 1 – Ф(x), где х =

По таблице можно найти данную величину:

= 2,6 n = []

 = 0.1 – это означает, что классы сильно пересекаются.

n = [] = 2700 для  = 0,1

Для  = 5 n = [] = 2

Подбирая размерность пространства всегда можно добиться уменьшения ошибок (с ростом размерности ошибка падает).

(X|2)

P₁^пр = f(U|1)dU

P_пр² = f(U|2)dU

P_пр^ср = q₁ P₁^пр + q₂ P₂^пр