
- •Кафедра моэвм Проф. Д.Т.Н .Геппенер в.В. «анализ и интерпретация данных»
- •1. Введение в анализ данных
- •1.1.Проблема обработки данных
- •1.2. Матрица данных
- •1.3. Гипотеза компактности и скрытых факторов
- •1.4. Структура матрицы данных и задачи обработки
- •1.5. Матрица объект – объект и признак – признак, расстояние и близость
- •1.6. Измерение признаков
- •1.7. Основные типы шкал
- •2. Классификация данных.
- •2.1. Постановка задачи
- •1. Линейные
- •2. Нелинейные решающие функции
- •2.2. Статистические методы классификации
- •2.2.1. Постановка задачи классификации как статистической задачи при известных вероятностных распределениях.
- •2.2.2. Построение классификации для нормального распределения.
- •2.2.3.Числовые примеры
- •2.2.4. Оценка качества классификации
- •2.2.5. Классификация на основе оценки апостериорной вероятности
- •2.2.6. Классификация двух нормальных распределений с неравными матрицами ковариации
- •2.2.7. Классификация нормально распределенных векторов при неизвестных параметрах распределения
- •2.2.8. Задача статистической классификации для количества классов больше 2
- •2.2.9. Линейная дискриминантная функция Фишера
- •3. Обучаемые классификаторы. Детерминистский подход.
- •3.1. Общие свойства линейных дискриминантных функций в детерминистской постановке.
- •3.2. Персептронный алгоритм получения линейных решающих правил
- •3.3. Правила поиска решения, основанные на минимизации градиента функции качества
- •3.3.1. Формальный вывод персептронного алгоритма
- •4. Кластерный анализ
- •4.1. Постановка задачи группировки данных
- •4.2 Пример
- •4.3. Критерии качества разбиения на классы
- •4.4. Основные типы кластерных процедур. Основные задачи кластерного анализа
- •4.4.1. Построение последовательной процедуры итеративной оптимизации
- •4.4.4. Иерархические процедуры группировки
- •4.4.4.1. Агломеративная процедура
- •4.5. Статистические модели группировки
- •4.6. Алгоритм автоматической классификации на основе использования кластер-анализа
- •5. Методы снижения размерности
- •5.1. Методы отбора признаков по заданному критерию
- •5.2. Метод главных компонент
- •6. Факторный анализ
- •6.1. Модель факторного анализа
- •6.2. Структура факторных уравнений
- •6.3 Неоднозначность факторного решения
- •6.4. Метод главных факторов
- •6.5. Метод центроидных факторов
- •7. Многомерное шкалирование
- •7.1. Дистанционная модель для различий
- •7.2. Модель Торгерсона
- •7.2.1.Поворот
- •7.2.2 Объективные повороты
- •7.2.3.Ручные повороты
- •7.2.4.Размерность
- •7.2.5.Интерпретация
- •7.3. Выводы
- •8. Литература
2. Классификация данных.
2.1. Постановка задачи
Рассматриваем матрицу данных:
x
![]()



 классы
классы
Мы должны каким-то образом разбить ее на классы. Эквивалентом термина классификация является распознавание образов.
Методы классификации используются для распознавания:
изображений;
речи;
букв;
Классификация данных: предполагается, что есть объект, описанный набором признаков:

в конечномерном пространстве Rn(можно решать задачу и в бесконечно-мерном пространстве , например, используя в качестве признаков коэффициенты ряда Фурье)
![]() .
.
Множество классов D представляет собой перечень возможных классов
![]() ,
,
где:
![]() определяют совокупность классов
определяют совокупность классов![]() .
.
Возможны следующие варианты:
![]()
![]() ,
то есть все задачи будем рассматривать
в
,
то есть все задачи будем рассматривать
в![]() .
Пусть имеется разбиение на классы:
.
Пусть имеется разбиение на классы:
![]()
Можно предполагать, что
![]() при
при![]() , то есть множества классов не пересекаются,
такую задачу мы хотим иметь, но чаще
всего это не наблюдается.
, то есть множества классов не пересекаются,
такую задачу мы хотим иметь, но чаще
всего это не наблюдается.




Часто имеет место
![]() ,
-это относится скорее к детерминированной
модели, когда множество классов не
покрывает все пространство
,
-это относится скорее к детерминированной
модели, когда множество классов не
покрывает все пространство
Если
![]() - такая ситуация тоже может быть, то
есть признаки покрывают все пространство.
- такая ситуация тоже может быть, то
есть признаки покрывают все пространство.
Для каждого
![]() мы должны найти некотороеdi,
которое определяется следующим образом:
мы должны найти некотороеdi,
которое определяется следующим образом:
![]() .
Задача состоит в построении такой
функции
.
Задача состоит в построении такой
функции
![]() и определенииdi.
Решение может быть однозначным
или неоднозначным. Такая функция
называется решающей.
и определенииdi.
Решение может быть однозначным
или неоднозначным. Такая функция
называется решающей.
Можно сформулировать следующую задачу: найти обратную функцию, порождающую для каждого номера (названия) соответствующее множество:
![]() ,
,
Эта функция должна порождать множество
![]() ,
которое соответствует определению
,
которое соответствует определению
класса di..
Идеальный вариант, когда выполнено
следующее:![]() ,
то есть совпадает с истинным множеством
класса, но чаще всего это не наблюдается.
,
то есть совпадает с истинным множеством
класса, но чаще всего это не наблюдается.
Р
 ешающая
функцияx2
ешающая
функцияx2
![]()



x1
Задача состоит в построении решающих функции.
Термин обучение заключается в следующем: есть обучающие выборки
![]() ,…,
,…,![]() ,…,
,…,![]() то
есть мы располагаем некоторыми конечными
множествами. Предварительно мы знаем,
куда относится какой-либо объект, нам
нужно построить конкретную решающую
функцию из
то
есть мы располагаем некоторыми конечными
множествами. Предварительно мы знаем,
куда относится какой-либо объект, нам
нужно построить конкретную решающую
функцию из![]() ,которая
будет удовлетворять определенным
критериям и
,которая
будет удовлетворять определенным
критериям и![]() (то
есть дает определенное решение).
(то
есть дает определенное решение).
Типы решающих функций:
Разбиение на 2 класса
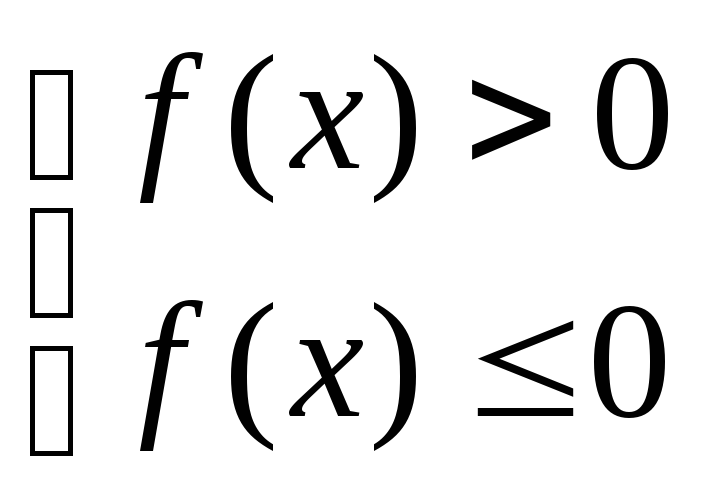
![]()
Если классов много, можно строить следующую функцию:
m– число классов
fi(x)i= 1..m
можно построить mрешающих функций и решение принимает следующий вид:







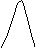








 Гауссовские функции
Гауссовские функции
То есть каждому классу сопоставляется Гауссовская функция.
![]()
Функции второго типа очень просто переходят в функции первого типа.
![]()




![]()
![]()





пустая область

![]()
![]()
Введем понятие границы между классами.
Граница между двумя классами определяется решающей функцией, разделяющей два этих класса fij(x)=0,соответственно:
f12(x)=0;
f23(x)=0;
f13(x)=0;
1-й класс может быть выбран следующим образом: очерчен на рис.(см. выше) жирной линией.
Оптимизационная задача
Наша задача заключается в том, чтобы построить класс функций, которые удовлетворяют некоторым критериям. Критериями могут быть
А) средние ошибки в результате классификации
Б) средний риск
В) получение на некотором множестве минимальное количество ошибок
Если имеется
![]() функционал
качества, то решается задача–
минимизировать функционал качества,
то есть найти
функционал
качества, то решается задача–
минимизировать функционал качества,
то есть найти![]() .
.
Пусть f– функция
определенного вида:
![]() ,
гдеai– параметры. То есть
,
гдеai– параметры. То есть
fможно задать параметрически и соответственно функционал качества имеет вид
![]() .
.
Таким образом, задача оптимизации
сводится к поиску
![]() .
Она может быть решена так:
.
Она может быть решена так:
![]() ,
где
,
где
![]() градиент
градиент
Существует много видов решения задач минимизации: градиентного спуска и т.д.
Существуют следующие виды параметрических функций f:
