4. Кластерный анализ
4.1. Постановка задачи группировки данных
Задача
состоит в том ,чтобы на основании данных
, находящихся в множестве Х разбить их
на m
групп таким образом , чтобы
Такое разбиение должно отвечать некоторому критерию сходства , т.е. элементы из одного класса отвечают критерию сходства, а элементы из разных классов- нет.
Имеется некоторая целевая функция, которая определяет правило, по которому мы относим элементы к тому или иному классу .Предполагается , что каждый элемент относится строго к одному классу- это детерминированная постановка задачи .
Кластеризация может быть и нечетной . Может быть вероятностная постановка задачи кластеризации .
Существует задача разделения смесей, когда по совместной выборке необходимо оценить характеристики классов.
Мы будем рассматривать кластерный анализ в детерминированном смысле .
Задача классификации может решаться очень успешно , если вначале провести кластеризацию.
Задача кластеризации:
1)Изучение данных
2)Использование кластеров для более правильного решения задачи классификации.
На чем базируется задача кластеризации:
Результат кластеризации зависит от критерия, по которому будет проходить кластеризация. Большинство методов основано на понятии расстояния между объектами.
4.2 Пример
Х={3,4,7,4,3,3,4,4}
Сумма квадратов отклонения:
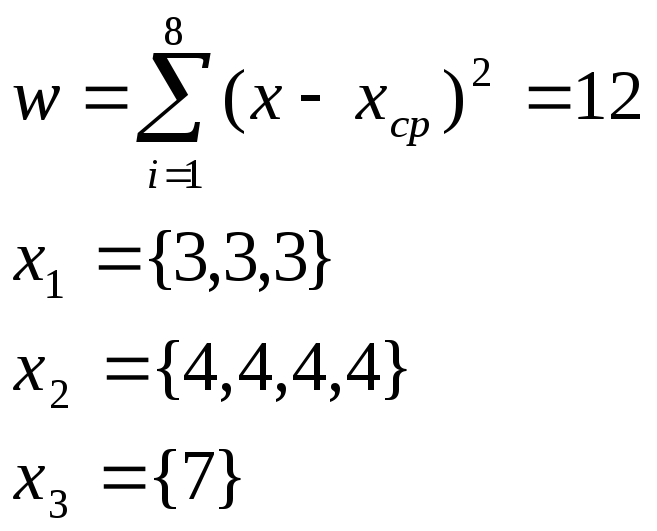
Внутригрупповые квадраты отклонения (критерий- это минимум внутригруппового отклонения)
w1=0
w2=0
w3=0
w=w1+w2+w3=0
Все метрические методы основаны функции расстояния между объектами.
Функция расстояния
При рассмотрении задачи кластеризации применяются различные функции расстояния.
|
N |
Наименование |
Формула |
|
1 |
Евклидово расстояние |
|
|
2 |
Квадрат Евклидова расстояния |
|
|
3 |
L1-норма |
|
|
4 |
Supremum |
Обычно Sup сводится к максимуму. (Расстояние Чебышева) |
|
5 |
Lp- расстояние (расстояние Минковского) |
|
|
6 |
|
|
|
7 |
Расстояние Махланобиса |
|
|
8 |
Для бинарных данных: расстояние Хемминга. |
|
-норма
Свойство расстояния Махланобиса:
заданы
это расстояние обладает свойством инвариантности по отношению к линейному преобразованию.
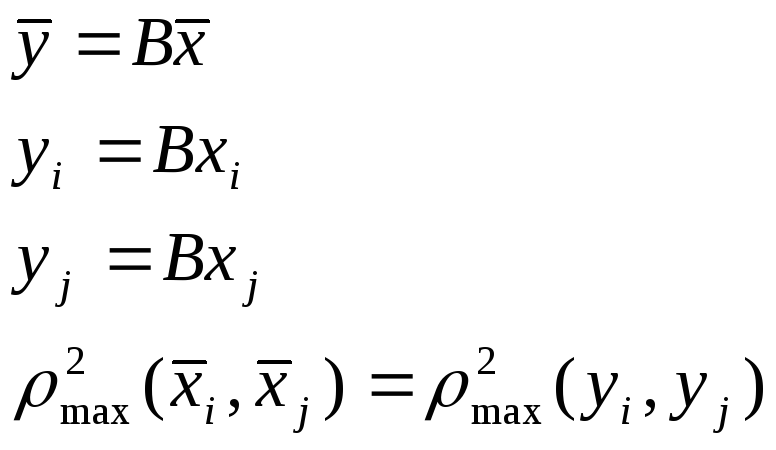
(Нужно
доказать свойство инвариантности.
Выписать формулы
и
т.д.)
Если имеется m объектов , то можно определить матрицу расстояний между этими объектами для каждой пары xi и xj
Условно
обозначим
Некоторые
алгоритмы работают на основе таких
матриц.
Мера
сходства определяется следующим образом:
и обладают следующими свойствами:
-коэффициент
корреляции.
Если
тоrij
определяется немного не так.
Меру сходства очень просто построить из меры расстояния:
Фактически это обратная функция
Может быть мера сходства для бинарных объектов , которая определяется следующим образом:
-число
совпадений единиц (если все совпадают,
то
=1,если
нет , то
=0)
-число
совпадений нулей
Что такое расстояние между кластерами:
Расстояние на основе ближайшего соседа – это расстояние , которое определяется минимальным расстоянием между элементами рассматриваемых кластеров.
Расстояние по принципу дальнего соседа(т.е. рассматриваются наиболее удаленные точки между объектами)
Расстояние между центрами тяжести (или между математическими ожиданиями)
средний
вектор.
Расстояние по принципу средней связи.
