
ИДЗ 1 Многопролётная балка
.pdf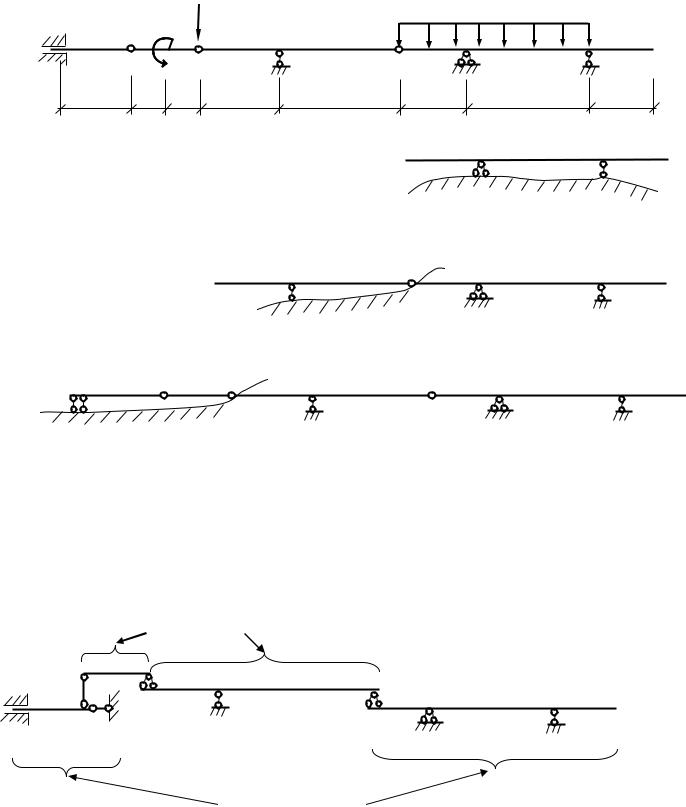
Расчёт статически определимой многопролетной балки на действие постоянных нагрузок с определением перемещений
Требуется:
1.Построить эпюры поперечных сил и изгибающих моментов.
2.При жесткости EI = 10000кНм2 определить вертикальное vC перемещения точки С и взаимный угол поворота θЕ точки Е.
|
|
F=10кН |
|
|
q=4кН/м |
|
|
M=8кНм |
|
|
|
|
|
|
|
|
|
|
|
|
А |
В |
С |
D |
Е |
F |
G |
|
2м 1м 1м 2м |
4м |
2м |
4м |
2м |
|
|
|
|
Решение |
|
|
|
1. Кинематический анализ |
|
Е |
F |
|
||
Диск ЕG соединяется с диском «земля» |
G |
|||||
тремя линейными связями, которые не |
|
Диск «земля» |
|
|||
пересекаются в одной точке и не параллельны |
|
|
|
|||
друг другу. Назовём эту геометрически неизменяемую систему «новая земля».
Диск |
СE С |
D |
Е |
|
присоединяется к диску |
|
|||
|
F |
G |
||
«новая |
земля» |
|
||
|
|
|
||
линейной |
связью и |
|
|
|
шарниром, не лежащим на линии связи. Назовём эту геометрически неизменяемую
систему «новая земля». |
С |
|
|
|
|
А |
В |
|
|
|
|
|
|
D |
Е |
F |
G |
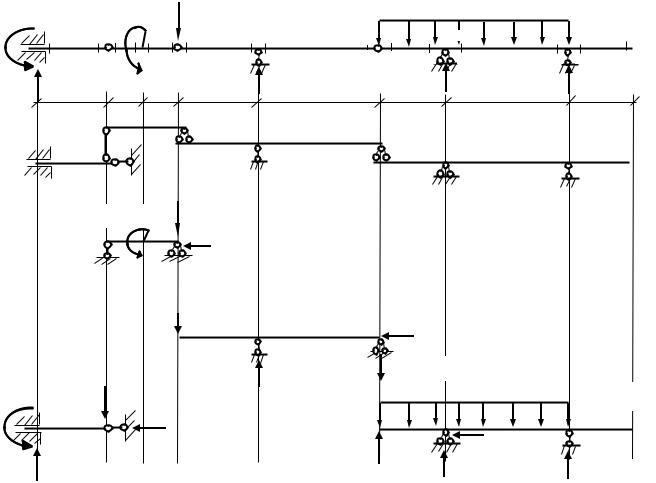
Диск АВ присоединяется к диску «земля» тремя линейными связями (две связи в точке А и связь ВС), не пересекающимися в одной точке и не параллельными. Геометрическая неизменяемость балки доказана.
2. Выбор рабочей схемы Рабочая или поэтажная схема – это схема взаимодействия элементов балки,
показывающая порядок передачи нагрузки от элемента к элементу.
Второстепенные элементы
|
С |
D |
Е |
|
А |
В |
|
F |
G |
|
|
Главные элементы |
|
|
1

Главными называют те элементы, которые могут самостоятельно воспринимать заданную нагрузку ( в данном случае - вертикальную).
Второстепенными называют элементы, которые теряют несущую способность, если отбросить соседние элементы.
3. Определение опорных реакций Расчёт производят, начиная с верхнего элемента, воздействие (опорная
реакция) передается от верхнего к нижнему элементу с обратным знаком (третий закон Ньютона).
y |
M=8кНм |
|
|
|
Элемент ВС |
|
|
∑Fx=0 => HC=0 |
||||||||||||
|
|
|
|
|
|
|
F=10кН |
|
|
|
|
|
|
|
|
|||||
В |
|
|
|
|
С |
x |
|
|
|
|
|
|
|
∑mB=0; -2VC-M+2F=0 => VC=6кН |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑mC=0; 2VB-M=0 => VB=4кН |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
VB=4кН |
|
|
|
|
VС=6кН |
|
|
|
|
|
|
|
Проверка: ∑Fy=0; VB +VC –F=0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
4+6-10=0 |
||||||||
|
|
|
1м |
1м |
|
|
|
|
|
|
|
|
|
|
0=0 - верно. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Элемент СE |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
∑Fx=0 => HE=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑mD=0; 4VE-2∙6=0 => =3кН |
|
|
|
|
6кН |
|
|
|
|
|
|
|
|
|
x |
∑mE=0; 4VD-6∙6=0 => =9кН |
|||||
|
|
|
|
|
|
С |
D |
|
|
Е |
|
|
|
|
|
Проверка: ∑Fy=0; VD+VE–6=0 |
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VE=3кН |
9-3-6=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
VD=9кН |
0=0 - верно. |
|||||||
|
|
|
|
|
|
|
|
|
|
2м |
|
4м |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Элемент АВ y
MA=8кНм 4кН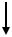
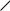 HВ=0 x
HВ=0 x
 А В
А В
VA=4кН
2м
∑Fx=0 => HB=0
∑mA=0; -MA+2∙4=0 => MA =8кНм ∑mB=0; -MA+2 VA =0 => VA =4кН Проверка: ∑Fy=0; VA–4=0
4-4=0 0=0 - верно.
Элемент EG
y |
q=4кН/м |
|
|
||
|
|
x |
Е F |
HF=0 |
G |
3кН |
|
|
|
|
|
|
VF=13,5кН |
VG=7,5кН |
2м |
4м |
2м |
∑Fx=0 => HF=0
∑mF=0; -4VG+2∙3+1∙6q=0 => VG =7,5кН ∑mG=0; 4VF+6∙3-3∙6q=0 => VF =13,5кН Проверка: ∑Fy=0; VF+VG–6∙4+3=0
13,5+7,5+3-24=0 0=0 - верно.
4. Построение эпюр Q и M
Правила знаков для внутренних усилий.
Поперечное внутреннее усилие (Q) будет положительным при стремлении вращать элемент по часовой стрелке и отрицательным в случае вращения против хода часовой стрелки. 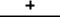

2

Поперечное внутреннее усилие (Q) в любом сечении равно алгебраической сумме проекций всех внешних сил, взятых по одну сторону от сечения, на поперечную ось стержня.
Изгибающий момент (M) будет положительным при растяжении нижних волокон и отрицательным в противном случае. 

Изгибающий момент (M) в любом сечении равен 




 алгебраической сумме моментов всех внешних сил, взятых по одну сторону от сечения относительно центра тяжести поперечного
алгебраической сумме моментов всех внешних сил, взятых по одну сторону от сечения относительно центра тяжести поперечного
сечения стержня. Эпюру изгибающих моментов строят на растянутых волокнах, знак на эпюру не выставляют.
При построении эпюр необходимо соблюдать некоторые правила. Если на расчётной схеме приложена сосредоточенная сила (в том числе и опорная реакция), то на эпюре поперечных сил соответственно в этом сечении будет скачок, равный величине этой силы, а на эпюре моментов - излом. Под сосредоточенным моментом на эпюре моментов будет скачок, равный величине этого момента. Грузовому участку, в пределах которого действует равномерно распределённая нагрузка, на эпюре поперечной силы соответствует участок с наклонной прямой (прямолинейная зависимость), а на эпюре моментов – парабола (квадратичная зависимость). При построении эпюр необходимо строго следить за выполнением дифференциальных
зависимостей: |
dM (x) |
Q(x) tg ; |
dQ(x) |
q tg . |
|
dx |
dx |
||||
|
|
|
Геометрическим смыслом первой производной функции является тангенс угла наклона касательной к графику функции. В случае, когда первая производная обращается в ноль, функция имеет экстремум.
При построении эпюр изгибающих моментов, имеющих участки с параболой необходимо соблюдать правило «паруса». Оно сводится к следующему. Равномерно распределенная нагрузка условно принимается за ветер, а парабола – за парус. Куда дует ветер, туда и прогибается парус.
Разобьём балку на грузовые участки. В настоящей балке можно выделить восемь грузовых участков. В начале и конце каждого грузового участка назначим сечения, в которых будем определять значения внутренних усилий. Можно рассматривать отдельно однопролётные балки и получать внутренние усилия для каждой как это делалось в курсе «Сопротивления материалов». А можно рассмотреть всю балку одновременно, но в этом случае будут более громоздкие выражения.
Для построения эпюры поперечных сил будем рассматривать равновесие левой отсечённой части. Т.к. VA стремится вращать отсечённую часть по часовой стрелке, то знак на эпюре поперечных сил будет положительный, в сечении 1-1 на эпюре имеет место скачок, равный величине опорной реакции (4кН), Q1-1 = Q2-2 = Q3-3 = =Q4-4 = Q5-5 = Q6-6= VA = 4кН. Сила F отражается на эпюре поперечных сил в виде скачка Q7-7 = Q8-8 = VA – F = 4 - 10 = - 6кН. В точке D на эпюре опорная реакция VD
отображается в виде скачка, Q9-9 = Q10-10 = Q11-11 = VA – F + VD = 4 – 10 + 9 = 3кН. На участке EF внутреннее поперечное усилие меняется по линейному закону Q = 3 – qx,
Q12-12 = 3 - 4·2 = -5кН. В точке F на эпюре имеет место скачок, равный величине опорной реакции VF, Q13-13 = -5 + 13,5 = 8,5кН. В пределах грузового участка FG
3
внутреннее поперечное усилие подчиняется линейному закону Q = 8,5 – qx, Q14-14 = 8,5 - 4·4 = - 7,5кН. В точке G на эпюре опорная реакция VG отображается в виде скачка, Q15-15 = Q16-16 = -7,5 + 7,5 = 0.
MA=8кНм M=8кНм |
|
F=10кН |
|
|
|
|
|
|
|
q=4кН/м |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
D |
10 |
11 |
12 |
13 F |
14 |
15G |
16 |
|
А |
В |
|
|
С |
Е |
|
|
|||||||||
VA=4кН |
|
|
|
|
VD=9кН |
|
|
VF=13,5кН |
VG=7,5кН |
||||||||
2м |
|
1м 1м |
|
2м |
|
|
4м |
|
|
2м |
|
4м |
2м |
|
|||
|
|
|
|
|
|
|
|
|
|||||||||
|
С |
D |
|
|
А |
В |
Е |
F |
G |
М=8кНм F=10кН
HC=0
VB=4кН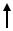
 VС=6кН
VС=6кН
|
6кН |
HE=0 |
|
|
VD=9кН |
VE=3кН |
|
MA=8кНм |
q=4кН/м |
||
4кНHВ=0 |
|||
|
|
||
|
3кН |
HF=0 |
|
VA=4кН |
|
VF=13,5кН VG=7,5кН |
Для построения эпюры изгибающих моментов будем рассматривать вначале равновесие левой отсечённой части. В сечении 1-1 имеет место скачок, вызванный реактивным моментом МА, момент растягивает верхние волокна (в уравнении
присвоим знак «-») М1-1 = 8кН·м. М2-2 = М3-3 = - МА + VA·2= - 8 + 4·2 = 0 (врезной шарнир, возможен поворот, поэтому изгибающий момент нулевой). М4-4 = - МА +
VA·3= - 8 + 4·3 = 4кН·м (растянуты нижние волокна). Между сечением 4-4 и 5-5 приложен сосредоточенный момент, его наличие приводит к скачку на эпюре
моментов, М5-5 = - МА + VA·3 – М = - 8 + 4·3 - 8 = - 4кН·м (растянуты верхние волокна). Наличие сосредоточенной силы отображается в виде излома на эпюре
моментов, М6-6 = М7-7 = - МА + VA·4 - М = - 8 + 4·4 - 8 = 0 (т.к. врезной шарнир). Между сечением 8-8 и 9-9 действует опорная реакция, её наличие приводит к
излому на эпюре моментов, М8-8 = М9-9 = - МА + VA·6 - М - F·2 = - 8 + 4·6 - 8 -10·2 = - 12кН·м (растянуты верхние волокна). Между сечением 10-10 и11-11 на расчётной
схеме имеется врезной шарнир, поэтому момент нулевой, М10-10 = М11-11 = - МА + VA·10 - М - F·6 + VD·4 = - 8 + 4·10 - 8 -10·6 + 9·4 = 0. Рассмотрим равновесие правой отсечённой части. Часть балки правее точки G не загружена, не деформируется,
поэтому М16-16 = М15-15 = М14-14 = 0. На участках FG и EF внутреннее усилие – изгибающий момент, описывается квадратным уравнением. Т.к. и на том, и на
4
другом участке в некоторых сечениях поперечное усилие обращается в ноль, а
dM (x) |
Q(x), то функция изгибающих моментов имеет в этих точках экстремум. |
|
dx |
||
|
Определим экстремальное значение момента на участке FG, М(x = 1,875м) = VG· x - - q· x 2/2= 7,5·1,875· - 4·1,8752/2 = 7,031кН·м. М13-13 = М12-12 = VG·4 - q·42/2 = 7,5·4 - - 4·42/2 = -2 кН·м. Экстремальное значение момента на участке EF составит М (x =
1,25м) = VG·(4 + x)-q·(4 + x)2/2 + VF·1,25 = 7,5·5,25 - 4·5,252/2 + 13,5·1,25 =
1,125кН·м. Полученные значения откладывают в масштабе.
MA=8кНм |
M=8кНм |
|
F=10кН |
|
|
|
|
|
q=4кН/м |
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
1А |
2 |
3 |
4 |
5 |
6 7 |
8 |
9 D |
10 |
11 |
12 |
13F |
14 |
15G |
16 |
|
|
|
|
|||||||||||||
VA=4кН |
В |
|
С |
|
VD=9кН |
Е |
|
|
VF=13,5кН |
VG=7,5кН |
|||||
|
|
|
|
|
|
|
|
|
|||||||
2м |
|
1м 1м |
|
|
2м |
4м |
|
|
2м |
|
4м |
2м |
|
||
|
|
|
|
|
|
|
|
Эпюра Q [кН] |
|
8,5 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
4 |
|
|
3 |
|
3 |
VF |
|
|
|
|
|
VA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
VD |
|
|
|
|
|
VG |
|
|
|
|
|
|
|
|
|
|
|
|
5 / q =5 |
|
|
||
|
|
|
|
|
|
6 |
6 |
|
3 / q = |
7,5 / q = |
7,5 |
|
|||
|
|
|
|
|
|
|
|
|
= 0,75м |
= 1, 25м |
= 1,875м |
|
|
||
|
|
|
|
|
|
|
|
Эпюра М [кНм] |
|
|
|
|
|
||
12
8 |
|
|
|
|
|
|
МА |
|
4 |
|
|
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
М |
|
1,125 |
|
|
|
|
4 |
|
7, 031 |
|
|
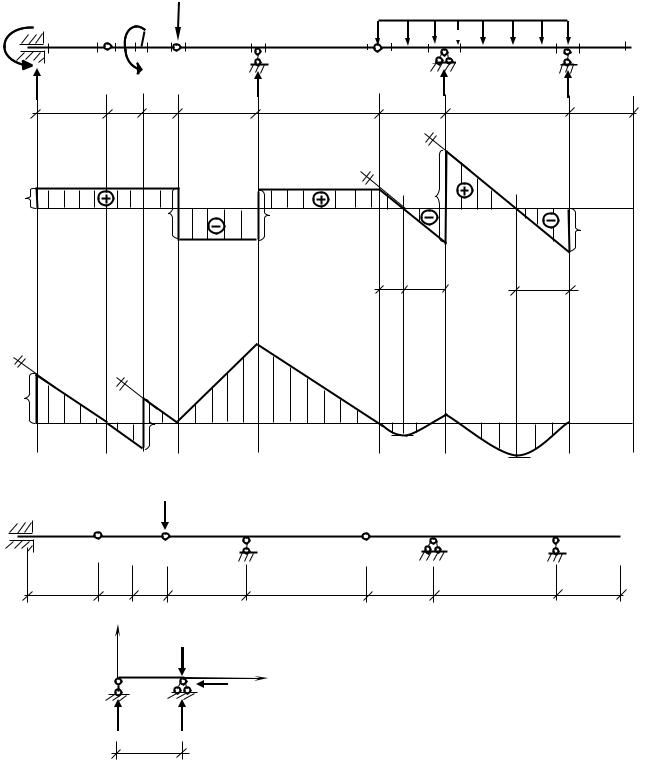
5. Определение перемещений |
|
|
|
|||
|
|
|
|
|||
|
|
i 1 1 |
|
|
|
|
А |
В |
С |
D |
Е |
F |
G |
|
2м 1м 1м 2м |
4м |
2м |
4м |
2м |
|
Элемент ВС |
y |
|
|
|
|
|
|
|
|
∑Fx=0 => HC=0 |
|
||
|
В |
i 1 1 С |
x |
|
||
|
∑mB=0; -2VC+2∙1=0 => VC=1; |
|||||
|
|
|
|
|||
|
|
HС=0 |
|
∑mC=0; 2VB=0 => VB=0; |
|
|
|
|
|
Проверка: ∑Fy=0; VB +VC-i1=0 |
|||
|
VB=0 |
VС=1 |
|
|||
|
|
|
0+1-1=0 |
|||
|
|
2м |
|
|
||
|
|
|
|
0=0 |
- верно. |
|
|
|
|
|
|
||
5

Элемент СE |
|
y |
|
|
|
|
|
|
|
|
∑Fx=0 => HE=0; |
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
∑mD=0; 4VE-2∙1=0 |
||
|
|
|
|
|
|
|
|
|
x |
|
VE =1/2; |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
С |
D |
|
|
|
Е |
HE=0 |
∑mE=0; 4VD-6∙1=0 |
|||
|
|
|
|
|
|
|
VD =3/2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
VE=1/2 |
|
||
|
|
|
|
|
VD=3/2 |
|
|
|
Проверка: |
||||
|
|
|
|
2м |
|
|
4м |
|
|
|
|
∑Fy=0; VD+VE–1=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3/2-1/2-1=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0=0 - верно. |
Элемент АВ |
|
|
|
|
|
|
y Элемент EG |
|
|
||||
|
y |
0 |
HВ=0 |
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
Е |
F |
|
|
G |
||
|
|
|
|
|
|
|
|
1/2 |
HF=0 |
|
|||
|
А |
В |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
VF=3/4 |
|
VG=1/4 |
|||
MA=0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
VA=0 |
|
|
|
|
|
|
|
|
2м |
|
|
|
|
|
|
|
|
|
|
|
|
|
4м |
2м |
|||
|
2м |
|
|
|
|
|
|
|
∑mF=0; -4VG+2∙1/2=0 => VG =1/4; |
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
∑mG=0; -4VF+6∙1/2=0 => VF =3/4; |
||||
|
|
|
|
|
|
|
|
|
|
Проверка: ∑Fy=0; VF+VG+1/2=0 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
-3/4+1/4+1/2=0 |
|
|
|
|
i 1 1 |
|
|
|
|
|
|
|
|
0=0 - верно. |
|
А |
В |
С |
|
D |
|
|
Е |
|
|
F |
|
G |
|
2м 1м 1м 2м |
|
4м |
|
|
|
2м |
4м |
2м |
||||
|
|
В |
i 1 1 |
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
HС=0 |
|
|
|
|
|
|
|
|
|
|
VB=0 |
|
VС=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
D |
|
|
Е |
|
HE=0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
HВ=0 |
|
VD=3/2 |
|
|
VE=1/2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MA=0 |
А |
В |
|
|
|
|
|
1/2 |
Е |
F |
HF=0 |
|
G |
|
|
|
|
|
|
|
|
|
|
|
|||
VA=0 |
|
|
|
|
|
|
|
|
VF=3/4 |
|
VG=1/4 |
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
Э п. |
М i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
i 3 1 |
|
|
|
|
|
|
А |
В |
|
С |
D |
|
|
Е |
|
|
F |
G |
|
|
|
2м 1м 1м 2м |
4м |
|
|
|
2м |
4м |
2м |
||||
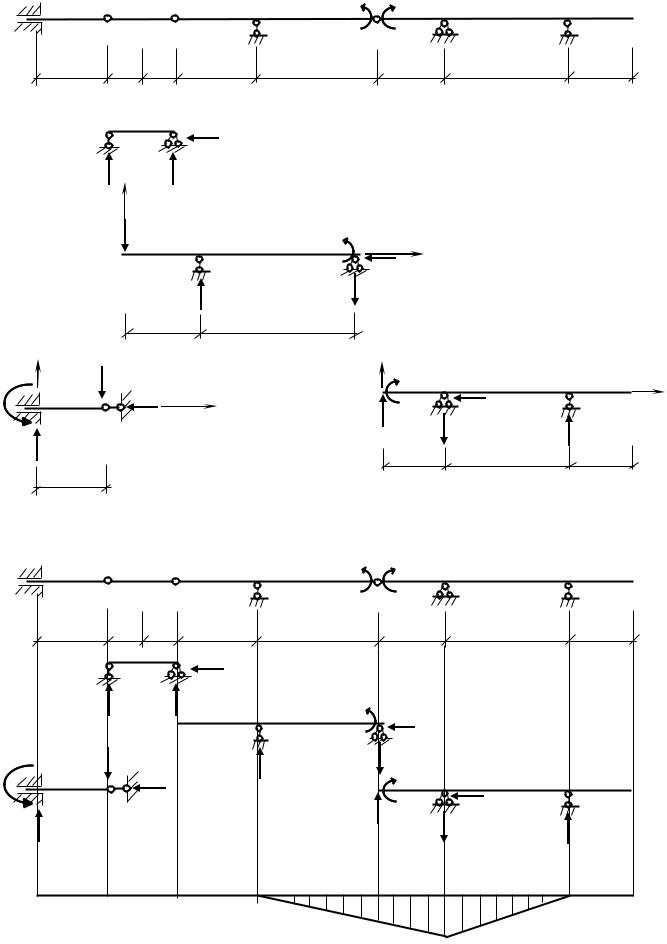
Элемент ВС |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
В |
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
HС=0 |
|
|
|
|
|
|
|
|
|
|
|
VB=0 |
y |
VС=0 |
|
|
|
|
|
|
|
|
|
Элемент СE |
|
|
|
|
|
|
|
|
|
∑Fx=0 => HE=0; |
|||
|
|
|
|
i 3 1 |
|
|
|
|
|||||
|
|
0 |
|
|
|
|
|
x |
|
∑mD=0; 4VE-1=0 => VE =1/4; |
|||
|
|
|
|
|
|
|
|
|
|
|
∑mE=0; 4VD-1=0 => VD =1/4; |
||
|
|
С |
|
D |
|
Е |
|
HE=0 |
|
|
Проверка: |
||
|
|
|
|
|
VD=1/4 |
|
|
VE=1/4 |
|
∑Fy=0; VD-VE=0 |
|||
|
|
|
|
|
|
|
|
1/4-1/4=0 |
|||||
|
|
|
|
2м |
4м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0=0 - верно. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Элемент АВ |
|
|
|
|
|
|
y |
Элемент EG |
|
||||
|
y |
0 |
|
|
|
|
|
|
i 3 |
1 |
x |
||
|
|
HВ=0 |
x |
|
|
|
|
||||||
|
|
|
|
|
Е |
|
|
F |
|
G |
|||
|
|
|
|
|
|
|
|
|
|
HF=0 |
|||
|
А |
В |
|
|
|
|
|
|
1/4 |
|
|
||
MA=0 |
|
|
|
|
|
|
|
VF=5/8 |
VG=3/8 |
||||
VA=0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
2м |
4м |
2м |
|||
|
2м |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
∑mF=0; -4VG+2∙1/4+1=0 => VG =3/8; |
||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
∑mG=0; 1-4VF+6∙1/4=0 => VF =5/8; |
||||
|
|
|
|
|
|
|
|
|
|
Проверка: ∑Fy=0; VF+VG+1/2=0 |
|||
|
|
|
|
|
|
|
|
i 3 1 |
|
|
|
-5/8+3/8+1/4=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0=0 - верно. |
|
А |
В |
|
С |
D |
|
|
Е |
|
|
F |
G |
|
|
|
2м 1м 1м 2м |
4м |
|
|
|
2м |
4м |
2м |
||||
|
|
В |
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
HС=0 |
|
|
|
|
|
|
|
|
|
|
VB=0 |
|
VС=0 |
|
|
|
i 3 1 |
|
|
|
||
|
|
|
|
С |
D |
|
Е |
|
|
HE=0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
|
VD=1/4 |
VE=1/4 |
|
i 3 1 |
|
|
|||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
А |
В |
HВ=0 |
|
|
Е |
|
|
F |
HF=0 |
G |
||
MA=0 |
|
|
|
|
1/4 |
||||||||
|
|
|
|
|
|
|
|
|
|
||||
VA=0 |
|
|
|
|
|
|
|
VF=5/8 |
VG=3/8 |
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Э п. М i 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1, 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
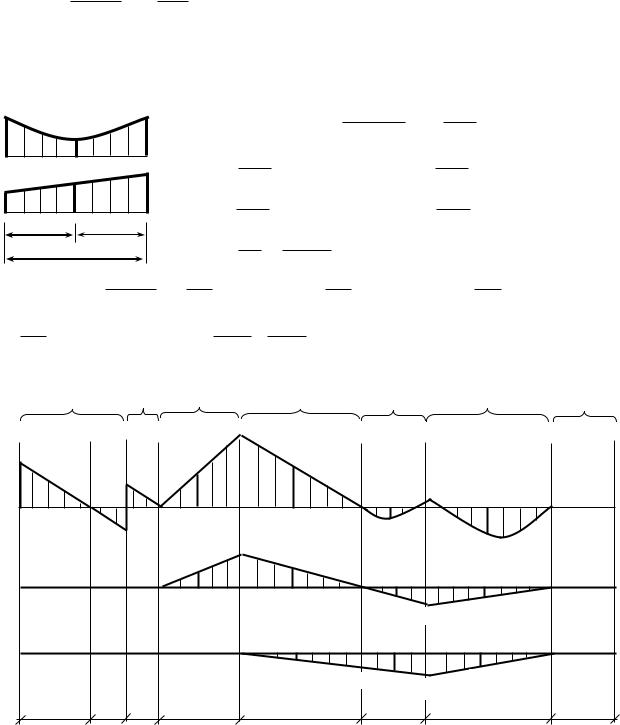
Перемещения (∆iF) находят как сумму интегралов от произведения функций |
||||||||||||||||||
изгибающих моментов, вызванных нагрузками и единичными силовыми |
||||||||||||||||||
воздействиями (i1, i3), отнесенного к жесткости (EI). Для сопряжения эпюр можно |
||||||||||||||||||
использовать формулу Симпсона и правило Верещагина (оба способа |
||||||||||||||||||
рассмотрены в курсе лекций). В настоящей работе применяется формула |
||||||||||||||||||
Симпсона, полученная для приближенного вычисления интеграла от |
||||||||||||||||||
произведения двух функций, заданных графически (в контексте примера речь |
||||||||||||||||||
идет об эпюрах изгибающих моментов). В рассматриваемой задаче график |
||||||||||||||||||
функции на грузовых участках это прямые линии либо параболы, а в таком случае |
||||||||||||||||||
формула Симпсона дает точное значение интеграла. Перемещения находят как |
||||||||||||||||||
i F |
Mi M F |
|
l |
|
|
|
cd ) , где Mi - функция изгибающих моментов |
|||||||||||
EI |
ds |
6EI |
(ab 4kf |
|||||||||||||||
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
от единичного силового воздействия, |
MF - |
функция изгибающих моментов от |
||||||||||||||||
нагрузок, |
l - длина грузового участка, |
EI - жесткость, |
a,b, k, f , c, d - приведены |
|||||||||||||||
ниже на рисунке. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a |
|
|
|
c |
|
|
i F vC M i1 M F ds |
l |
|
(ab 4kf cd ) |
||||||||
|
k |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
l |
EI |
|
|
6EI |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
2 |
(0 4 1 6 12 2) |
|
4 |
(12 2 4 6 |
1 0) |
||||||
|
|
f |
|
|
|
|
|
|||||||||||
b |
|
|
|
|
|
6EI |
|
|
|
|
|
6EI |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
l / 2 |
l / 2 |
|
|
|
6EI (0 4 1 0,5 2 1) |
6EI |
|
( 2 1 4 7 |
0,5 0) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
l |
|
|
|
|
40 |
|
40 |
0, 004 м 0, 4см. |
|
|||||||
|
|
|
|
|
|
|
EI |
|
10000 |
|
|
|
|
|
|
|
||
i F |
Е M i 3 M F ds |
l |
(ab 4kf cd ) |
4 (0 4 6 0,5 0) |
2 (0 4 11, 25 2 1,5) |
|||||||||||||
|
|
l |
EI |
|
6EI |
|
|
|
|
|
6EI |
|
|
|
|
|
6EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 (2 1,5 4 7 0,75 0) |
4,666 |
4,666 0,000466 рад 0,030. |
|
|
|
||||||||||||
6EI |
|
|
|
|
EI |
10000 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Э п. М [ кНм ] |
|
|
|
|
|
|
|||
|
|
I |
|
II |
III |
|
|
|
IV |
|
V |
|
|
|
|
VI |
VII |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
6 |
|
|
|
6 |
|
|
|
|
|
|
|
|
||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
2 |
|
|
Э п. |
М i 1 |
1 |
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Э п. |
М i 3 |
0,5 |
1 |
|
|
0,5 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
0,5 |
1 1, 25 |
1,5 |
|
0,75 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2м 1м 1м 2м |
|
|
|
4м |
|
2м |
|
|
|
|
4м |
2м |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
