Основы теории вероятностей и математической статистики

1.Случайное событие – это событие, которое при данных условиях может произойти, либо не произойти. Относительная частота событий называется вероятностью и показывает отношение числа ожидаемых событий к числу возможных.Статистическое определение вероятности подразумевает под собой вероятность как предел, к которому стремится относительная частота. При классическом определении отн. частота и вероятность совпадают. В этом случае должно быть известно должны быть известны полное число возможных событий и число ожидаемых событий (орёл-решка, кубики и тп).Совместные события могут происходить параллельно друг другу; несовместные события исключают появление друг друга в ходе проводимого опыта. Зависимым называется событие, на вероятность которого оказывает влияние исход какого-либо иного события. Независимые наоборот.

2.Теорема сложение вероятностей: вероятность появление какого-либо события из нескольких несовместных равна сумме их вероятностей (или то, или другое)Теорема умножения вероятностей: Вероятность совместного появления независимых событий равна произведению их вероятностей(и то и другое).Условная вероятность — вероятность одного события при условии, что другое событие уже произошло(опыт с шариками в мешке, которые вытаскивают и не возвращают)

3.Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины(возможные значения которой образуют конечную или бесконечную последовательность чисел). Закон распределения может быть задан аналитически, в виде таблицы или графически. Математическое ожидание имеет смысл среднего значения случайной величины. Для дискретных случ. величин оно определяется как сумма произведений случ. величины на вероятность её появления. Дисперсия описывает разброс случ. величин относительно математического ожидания. Дисперсия дискретных случ. величин определяется, как сумма квадратов разности случ. величин и математического ожидания на соответствующие вероятности появления этих случайных величин. Среднее квадратичное отклонение — это квадратный корень из среднего арифметического всех квадратов разностей между данными величинами и их средним арифметическим.

4. Непрерывные случайные величины всегда имеют вероятность равную нулю, поскольку количество её возможных численных значений бесконечно велико.Математическое ожидание имеет смысл среднего значения случайной величины. Для дискретных случ. величин оно определяется как сумма произведений случ. величины на вероятность её появления. Дисперсия описывает разброс случ. величин относительно математического ожидания. Дисперсия дискретных случ. величин определяется, как сумма квадратов разности случ. величин и математического ожидания на соответствующие вероятности появления этих случайных величин.Среднее квадратичное отклонение — это квадратный корень из среднего арифметического всех квадратов разностей между данными величинами и их средним арифметическим.

5. Случайная величина называется дискретной случайной величиной, если она принимает не более чем счетное число значений. Примеры:

1) дискретная случайная величина Бернулли(закон распределения Бернулли). Закон распределения дискретной случайной величины Бернулли имеет следующий вид: 0<p<1

Такому распределению соответствует бросание монеты, на одной стороне которой - 0, а на второй - 1.

2) дискретная биномиальная случайная величина (биномиальное распределение). Закон распределения данной дискретной случайной величины запишется следующим образом:

где

Число успехов в n испытаниях схемы Бернулли имеет биномиальное распределение.

3) дискретная случайная величина Пуассона(пуассоновское распределение с параметром ). Закон распределения дискретной случайной величины Пуассона задается следующим образом:

где - параметр.

Закон распределения случайной величины Пуассона носит название закона редких событий, например, число вызовов, поступивших на телефонную станцию, число распавшихся нестабильных частиц и т.д.

4) дискретная геометрическая случайная величина (геометрическое распределение). Закон распределения геометрической дискретной случайной величины имеет вид

Пусть производятся независимые испытания, причем в каждом испытании возможны два исхода - "успех" с вероятностью p или "неуспех" с вероятностью 1 - p , 0 < p < 1 . Обозначим через число испытаний до первого появления "успеха", тогда будет дискретной геометрической случайной величиной.

Распределение случайной величины называется непрерывным, а сама случайная величина - непрерывной случайной величиной, если для любого

где - интегрируемая по Лебегу функция. Функция называется плотностью распределения случайной величины.

Примеры

1) нормальная непрерывная случайная величина, или непрерывная случайная величина Гаусса(нормальное распределение).Важная роль этого распределения объясняется тем, что оно обычно возникает в явлениях, подверженных действию большого числа малых случайных величин. Так, математическая теория выборочного метода в статистике для расчета некоторых показателей широко использует нормальное распределение.

2)экспоненциальная (показательная) непрерывная случайная величина(экспоненциальное распределение).Экспоненциальному распределению подчиняется время распада ядер атомов различных элементов. Оно обладает важным свойством - отсутствием последствия. Несложно убедиться в том, что вероятность распада ядра за время при условии, что перед этим оно уже прожило время , совпадает с безусловной вероятностью распада того же самого ядра за время. Именно это свойство и представляет собой отсутствие последствия.

3) Равномерная на [a;b] непрерывная случайная величина(равномерное на отрезке [a;b] распределение).Равномерное распределение реализует принцип геометрической вероятности при бросании точки на отрезок [a;b].

Закон Бернулли: число ожидаемых событий, появляющихся в опытах с n независимыми испытаниями, в которых ожидаемые события характеризуются одинаковой вероятностью p или:

Математическое ожидание

Пусть — случайная величина, определённая на некотором вероятностном пространстве. Тогдагде символ M обозначает математическое ожидание.

6. смотри билет 5

Закон распределения Пуассона: удовлетворяет вероятности появления заданного количества редко происходящих случайных событий, наблюдаемых в серии из большого количества независимых повторных опытов. Вероятность намного меньше 1.

Где m-число ожидаемых событий, а- параметр распределения, совпадающий с математическим ожиданием, е-основание натурального логарифма. Распределению Пуассона удовлетворяют числа редких событий, происходящих за определённый промежуток времени.

7. Непрерывные и дискретные случайные величины. Плотность вероятности. Нормальный закон распределения. Математическое ожидание и дисперсия. Графическое представление. Примеры.

Дискретные случайные величины – величины, которые могут принимать счетное количество значений конечное или бесконечное. пример: количество пассажиров в транспорте.

Непрерывные случайные величины- величины. Которые принимают бесконечное число возможных значений в конечном, или в бесконечном интервалах изменения пример: время, масса, объем, температура тела.

Плотностью вероятности f(x) непрерывной случайной величины Х называется производная функции распределения F(X) этой величины: f(x)=F’(X)

Основные свойства плотности: 1). Плотность вероятности является неотрицательной функцией: f(x)>0 2) вероятность того, что в результате испытания непрерыв. Случ. Величина примет какое-либо значение из интервала(а,b), равна определенному интегралу(в пределах от а до b ) от плотности вероятности этой случайной величины.

3).определенный интеграл в пределах от минус бесконечности до плюс бесконечности от плоности вероятности непрерывной случайной величины равен единице..

4)определенный интеграл в пределах от «–« бесконечности до х от плотности вероятности непрерывной случайной величины равен функции распределения этой величины.

Нормальное распределение, также называемое распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:

где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.

Графики нормального распределения

Математическим ожиданием дискретной случайной величины называется сумма парных произведений всех возможных значений случайной величины на соответствующие им вероятности, т.е. * Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Пусть  — случайная величина, определённая на некотором вероятностном пространстве. Тогда где символ M обозначает математическое ожидание.

8. Стандартное нормальное распределение. Стандартные интервалы. Понятия доверительного интервала и доверительной вероятности.

Доверительный интервал — это интервал, построенный с помощью случайной выборки из распределения с неизвестным параметром, такой, что он содержит данный параметр с заданной вероятностью.

Пусть - выборка из некоторого распределения с плотностью , зависящей от параметра , который может изменяться в интервале . Пусть - некоторая статистика и - функция распределения случайной величины , когда выборка имеет распределение с плотностью . Предположим, что есть убывающая функция от параметра . Обозначим квантиль распределения , тогда есть возрастающая функция от . Зафиксируем близкое к нулю положительное число (например, 0,05 или 0,01). Пусть . При каждом неравенства

(1)

выполняются с вероятностью , близкой к единице. Перепишем неравенства (1) в другом виде:

(2)

Обозначим , и запишем (2) в следующем виде:

Интервал называется доверительным интервалом для параметра , а вероятность - доверительной вероятностью.

Нормальное распределение, также называемое распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:

где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.

Графики нормального распределения

9. Понятие генеральной совокупности и выборки. Объём выборки, репрезентативность. Статистическое распределение (вариационный ряд). Примеры. Характеристики выборки

Генеральной совокупностью называют множество каких либо однородных элементов, из которого по определенному правилу выделяется некоторая часть элементов. Называемая выборкой. Число таких выделяемых объектов называется объемом выборки. Выборка производится с целью описания генеральной совокупности. Если это описание является полным и корректным, то выборка называется репрезентативной.

Пример.при анализе забол-ти детей , определенной возрастной группы, ген.совокупностью являются данные осмотра всех детей данной возрастной группы, а выборкой являютя данные, полученные в пределах одного района.

Варианта – конкретное значение случайной величины

Вариац.ряд-варианты в определенном порядке. Вариационным (статистическим) рядом называется таблица, первая строка которой содержит в порядке возрастания элементы ', а вторая - их частоты (относительные частоты .

10. Оценка параметров генеральной совокупности по характеристикам её выборки (точечная и интервальная). (Параметры генеральной совокупности и характеристики выборки. Формулы, пояснения).

Интервальные оценки

По известной величине выборочной характеристики ( или и др.) можно определить интервал, в котором с той или иной вероятностью определяется значение параметра генеральной совокупности, оцениваемого по этой выборочной характеристике.

Вероятности, признанные достаточными для того, чтобы уверенно судить о генеральных параметрах на основании выборочных характеристик, называются доверительными.

Обычно в качестве доверительных вероятностей выбирают значения 0,95, 0,99 или 0,999 (их принято выражать в процентах). Перечисленным значениям соответствуют 95, 99 и 99,9 .

5.3. Точечные оценки .

Под термином “оценка” в теории оценок понимаются как сами значения параметров генеральной совокупности, полученные по выборке, так и процесс получения этих значений, т. е. правило, по которому они получены.

Оценки подразделяются на два класса; точечные и интервальные.

Точечные оценки представляют собой определенные значения параметров генеральной совокупности, полученные по выборочным данным. Эти значения должны быть максимально близки к значениям соответствующих параметров генеральной совокупности, которые являются истинными значениями оцениваемых параметров.

ряд требований:

1. Состоятельность. Точечная оценка a_В называется состоятельной, если при неограниченном увеличении объема выборки () она стремится к истинному значению параметра a.

2. Несмещенность. Оценка a_В называется несмещенной, если она не содержит систематической ошибки, т. е. среднее значение оценки, определенное по многократно повторенной выборке объема n из одной и той же генеральной совокупности, стремится к истинному значению соответствующего генерального параметра a.

3. Эффективность. Несмещенная оценка является эффективной, если она имеет наименьшую дисперсию по сравнению с другими несмещенными оценками того же параметра генеральной совокупности.

Параметры генеральной совокупности: дисперсия и матем. Ожидание.

11. Графические характеристики случайных величин. Гистограмма. Характеристики положения (мода, медиана, выборочная средняя).

Медиа́на (50-й процентиль, квантиль 0,5) — возможное значение признака, которое делит ранжированную совокупность (вариационный ряд выборки) на две равные части: 50 % «нижних» единиц ряда данных будут иметь значение признака не больше, чем медиана, а «верхние» 50 % — значения признака не меньше, чем медиана.

Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.

Полигоном частот называют ломаную линию, отрезки которой соединяют точки . Для построения полигона частот на оси абсцисс откладывают варианты , а на оси ординат – соответствующие им частоты и соединяют точки отрезками прямых.

Полигон относительных частот строится аналогично, за исключением того, что на оси ординат откладываются относительные частоты .

В случае непрерывного признака строится гистограмма, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала – сумму частот вариант, попавших в i–й интервал.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которой служат частичные интервалы длиною h, а высоты равны отношению . Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии (высоте) . Площадь i–го прямоугольника равна – сумме частот вариант i–о интервала, поэтому площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

Модой случайной величины называется её наиболее вероятное значение. Термин «наиболее вероятное значение», строго говоря, применим только к прерывным величинам; для непрерывной величины модой является то значение, в котором плотность вероятности максимальна. Условимся обозначать моду буквой . На рис. 5.6.1 и 5.6.2 показана мода соответственно для прерывной и непрерывной случайных величин.

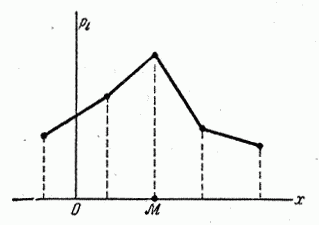
Рис. 5.6.1

В качестве точечной оценки для “a” берут выборочную среднюю .

Def: выборочной средней называется среднее арифметическое выборки.

(2)

Теорема: выборочная средняя является состоятельной и несмещенной оценкой математического ожидания .

12. Понятие о задаче статистической проверки гипотез. Нулевая и альтернативная гипотезы. Оценка достоверности различий по t-критерию Стьюдента

Нулевая гипотеза подразумевает под собой следующее: формально выдвигается предположение о принадлежности двух исследуемых выборок одной и той же генеральной совокупности и определяется доверительная вероятность принятия или отвержения этой гипотезы. Нулевая гипотеза отвергается, если используя метод доверительных интервалов с заданной доверительной вероятностью, эти интервалы не пересекаются.

Альтернативная гипотеза— это предположение, принимаемое в случае отклонения нулевой гипотезы. Альтернативная гипотеза утверждает положительную связь между изучаемыми переменными. "Температура воздуха зависит от интенсивности солнечного излучения" -это альтернативная гипотеза. Понятие о задаче статистической проверки гипотез. Нулевая и альтернативная гипотезы. Оценка достоверности различий по t-критерию Стьюдента.

Нулевая гипотеза подразумевает под собой следующее: формально выдвигается предположение о принадлежности двух исследуемых выборок одной и той же генеральной совокупности и определяется доверительная вероятность принятия или отвержения этой гипотезы. Нулевая гипотеза отвергается, если используя метод доверительных интервалов с заданной доверительной вероятностью, эти интервалы не пересекаются.

Этот критерий относится к параметрическим и предполагает, что генеральные совокупности сравниваемых выборок распределены по нормальному закону, а отличие их дисперсий является незначительным. Тогда t - критерий определяется по формуле

t_k - переменная величина, следующая t - распределению Стьюдента с числом степеней свободы

k = (n₁-1)+(n₂-1) = n₁+n₂ -2, а коэффициент N₁₂ равен

Нулевую гипотезу отвергают, если фактически установленная величина t_k превзойдет критическое значение этой величины t_ak для принятого значения доверительной вероятности (а) и числа степеней свободы k = n₁ +n₂ -2, то есть при условии t_ak > \t_k\. Если же наблюдается соотношение t_ak <\t_k\, то оснований отвергнуть Н₀ с заданным уровнем доверительной вероятности ос не имеется. Критические значения t_ak приводятся в специальных таблицах. (Например, такая таблица дана в приложении 4 к данному пособию).

Если дисперсии сравниваемых групп не равны, то величину t - критерия находят по формуле:

Число степеней свободы вычисляют по следующим формулам:

1. При n₁=n₂

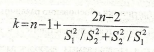
1. При n₁=/=n₂

Механика жидкостей и газов. Акустика.

Дифракция звука - отклонение распр.звука от законов геом. акустики , обусловл. его волновой природой. Рез-ты - расхождение зв. пучков при удалении от излучателя.

Интерференция звука - неравномер-ть простран. распределния ампл., результирующий зв. волны в завис-и от соотн. Между фазами волн,с кладыв. В тот или иной точке простр-ва.

Звук - колебания с частотой от 16 Гц до 20 кГц, распространяющихся в упругой среде.

Виды звуков: тоны, шумы, звуковые удары.

Волновое сопротивление

Объективные характеристики звука-характеристики,не зависящие от св-в приёмника:

1)Интенсивность(сила звука)-энергия,принимаемая зв. Волной за 1 времени через 1 площади,установл. перпенд. вол. звука[Вт/м²];

2)Частота основного тона [Гц];

3)Спектр звука - кол-во обертонов;

Ультразвук - механические колебания и волны, частоты кот. От 2*10⁴ до 10¹⁰ Гц.

Физические основы применения УЗ в медицине:

Идеальная жидкость - жидкость, лишенная вязкости и теплопроводности.

Существует ряд уравнений, описывающих течение идеальной жидкости по трубкам.

1) Условие неразрывности струи: при стационарном течении несжимаемой жидкости через любые сечения трубки тока, каждую секунду протекают одинаковые объемы жидкости, равные произведению площади сечения () на среднюю скорость движения ее частиц ().

- уравнение неразрывности струи.

Если жидкость движется по системе последовательно соединенных трубок различного сечения, то скорость ее движения обратно пропорциональна площади сечения трубок (рис. 2.1).

сечение 2

сечение 1

Рис. 2.1. Движение жидкости в трубе с разными сечениями (длина стрелок изображает среднюю скорость течения жидкости)

Площадь сечения пропорциональна квадрату диаметра трубки , поэтому если диаметр трубки в сечении 2 вдвое меньше, чем в сечении 1, то площадь поперечного сечения 2 в четыре раза меньше, чем площадь сечения 1. Следовательно, и скорость потока в сечении 2 будет в четыре раза больше, чем в сечении 1.

2) Для идеальной жидкости (сила трения полностью отсутствует) справедливо уравнение, которое было получено швейцарским математиком и физиком Даниилом Бернулли (1700 - 1782). Рассмотрим тонкую трубку тока и выделим в ней два произвольных сечения (рис. 2.2).

В общем случае эти сечения находятся на различных высотах (h₁ и h₂), и их площади различны (S₁ и S₂). Вследствие уравнения неразрывности, различны будут и скорости течения жидкости в этих сечениях ( и ). Обозначим давления жидкости в этих сечениях P₁ и Р₂, соответственно.

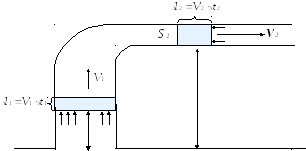
P₂

сечение Б

S₁

h₂

P₁

сечение А h₁

Рис. 2.2. Параметры сечений в трубке тока

Выделим в трубке тока малый объём жидкости _ΔV, массой _Δm, который перемещается из положения А в положение Б (рис. 2.2). _ΔV = S₁·_Δl₁ = S₂·_Δl₂

Из-за малости объёма _ΔV,можно считать, что сечения трубки S₁ и S₂ на протяжении отрезков _Δl₁ и _Δl₂ постоянны.

Перемещение массы _Δm жидкости происходит под действием разности внешних сил давления в сечениях А и Б (давление Р₂ противодействует движению жидкости).

Сила давления в сечении А: F_P1 = P₁·S₁; в сечении Б: F_P2 = P₂·S₂. F_P1> F_P2

За время _Δt частицы жидкости перемещаются в сечении А на расстояние ,в сечении Б на расстояние

Работа силы давления: А = F_P1 ·_Δl₁ - F_P2·_Δl₂ = ,

так как , тоA = P₁· _ΔV - P₂· _ΔV

Эта работа затрачивается на изменение потенциальной и кинетической энергии массы _Δm при переходе из положения Б в положение А (из конечного вычитаем начальное).

Перенесём, все компоненты, относящиеся к сечению А, в левую часть уравнения, а компоненты, относящиеся к сечению Б - в правую часть.

разделим всё уравнение на _ΔV, получим:

Положения А и Б выбраны произвольно, значит можно утверждать, что в любом месте вдоль трубки сохраняется условие:

- это уравнение Бернулли,

где Р - статическое давление, ρgh - гидростатическое давление, обусловленное движением жидкости, а - динамическое давление.

Уравнение Бернулли формулируется так: при стационарном течении идеальной жидкости полное давление, равное сумме статического, динамического и гидростатического давлений, одинаково во всех поперечных сечениях трубки тока.

Методы измерения статического давления и скорости жидкости

Установим в разных местах горизонтальной цилиндрической трубы (струи жидкости) одного сечения две трубки: 1) манометрическую трубку, плоскость отверстия которой расположена параллельно движению жидкости; 2) трубку, изогнутую под прямым углом навстречу движению жидкости (трубку Пито) (рис. 2.6).

1)

2)

Рис. 11.6. Измерение скорости жидкости

Манометрическая трубка позволяет измерить статическое давление Р_статич, Трубка Пито (изогнутая) позволяет измерить полное давление Р_полное, равное в данном случае сумме статического и динамического давлений. Так как труба горизонтальна, a = 0, то имеем:

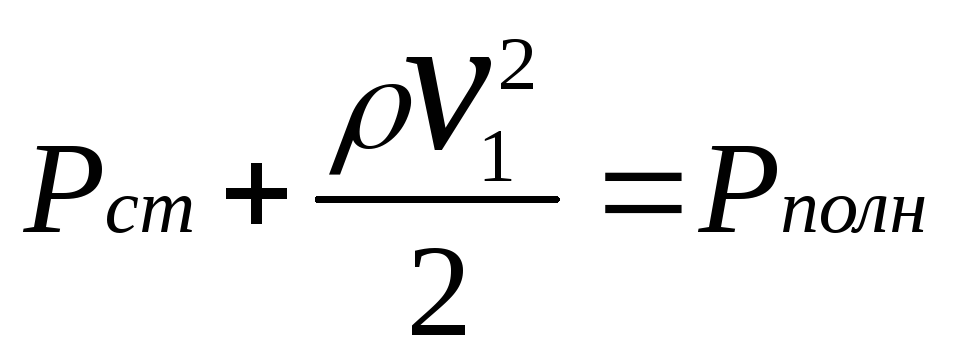, откуда .

Имея систему двух таких трубок, вычисляют скорость потока жидкости.

Течение жидкости называется установившемся, стационарным, если скорости частиц в каждой точке потока со временем не изменяются (при этом условии линии тока совпадают с траекториями частиц жидкости).

Вязкость (внутреннее трение) жидкости - свойство жидкости оказывать сопротивление перемещению одной ее части относительно другой.

Движение реальной жидкости при малых скоростях носит слоистый (ламинарный) характер. При установившемся ламинарном течении бесконечно малые слои жидкости скользят относительно друг друга, не перемешиваясь, и сохраняют во времени свои пространственные положения. При возрастании различия в скоростях соприкасающихся слоёв, силы трения между ними также возрастают. Это приводит к тому, что при некоторой критической величине скоростей, разной для разных жидкостей, характер течения существенно меняется. Возникает энергичное перемешивание слоёв жидкости. Положение слоёв в пространстве с течением времени постоянно меняется, появляются вихри. Такое движение называется турбулентным.

Важным свойством турбулентного течения (в сравнении с ламинарным) является высокое сопротивление потоку. Если бы удалось «погасить» турбулентность, то удалось бы достичь огромной экономии мощности двигателей кораблей, подводных лодок, самолетов.

Ньютоновская жидкость:вода.

Неньтоновские жидкости:кровь.

Сила внутреннего трения; закон Ньютона

Предположим, что в ламинарном установившемся потоке жидкости два соприкасающихся слоя имеют скорости V₁ u V₂ (рис. 1.1).

x dV

dx

V₀ V

Тогда со стороны слоя 1, движущёгося более быстро, на слой 2, движущийся медленнее, действует ускоряющая сила F₁. Наоборот, со стороны слоя 2, движущегося медленнее, на более быстрый слой 1 действует задерживающая сила F₂. Эти силы внутреннего трения направлены вдоль поверхности соприкосновения слоёв в противоположные стороны и по третьему закону Ньютона их величины одинаковы, то есть F₁=F₂=F_тр

Величина силы внутреннего трения F_тр, возникающая в плоскости соприкосновения двух скользящих относительно друг друга слоёв жидкости прямо пропорциональна площади их соприкосновения S, величине градиента скорости и зависит от рода жидкости:

где  - коэффициент внутреннего трения (вязкость) жидкости.

Уравнение называют законом Ньютона для течения вязкой жидкости. Ньютон получил это уравнение экспериментально. Градиент скорости - показывает изменение скорости слоев жидкости на единице длины и направлен перпендикулярно движению слоев в сторону возрастания скорости движения.

Из уравнения видно, что при возрастании скорости движения слоёв жидкости, при увеличении площади соприкосновения этих слоёв и при увеличении коэффициента вязкости жидкости сила трения возрастает. Следует упомянуть, что на силу трения влияет температура жидкости. При повышении температуры сильно возрастает подвижность молекул, что, в свою очередь, влечёт за собой уменьшение вязкости жидкостей (), поэтому эксперименты следует проводить при стабильной температуре.

Число Рейнольдса

Характер течения жидкости по трубе зависит от свойств жидкости, скорости ее течения, размеров трубы. Английский физик и инженер Осборн Рейнольдс (1842-1912) изучал переход от ламинарной формы течения к турбулентной. Он экспериментально показал, что турбулентность возникает, когда определенная комбинация величин, характеризующих движение, превосходит некоторое критическое значение. Им было введено безразмерное число, позднее названное в его честь числом Рейнольдса, которое характеризует течение жидкости по трубе (каналу).

Число Рейнольдса определяется по формуле: ,

где ρ_ж - плотность жидкости, η - ее вязкость, V - скорость течения, D - диаметр трубы.

Это число является критерием вида течения. Существует критическое значение числа Рейнольдса: для гладких цилиндрических труб Re_Kp = 2300. Если число Рейнольдса больше критического, то движение жидкости турбулентное, если меньше, то ламинарное. Например, при атеросклерозе критическое число Рейнольдса в некоторых сосудах становится равным 1160.

Так как число Рейнольдса зависит от вязкости и плотности жидкости, то удобно использовать в этой формуле кинематическую вязкость: . Тогда число Рейнольдса можно записать в виде . Кинематическая вязкость полнее, чем динамическая, учитывает влияние внутреннего трения на характер течения жидкости или газа. Так, динамическая вязкость воды приблизительно в 100 раз больше, чем воздуха (при 0°С), но кинематическая вязкость воды в 10 раз меньше, чем воздуха, и поэтому кинематическая вязкость сильнее влияет на характер течения воздуха, чем воды.

10.формула стокса. Подробно объяснить ход работы по определению коэффициента вязкости жидкостей методом Стокса. Дать формулу для вычисления коэффициента вязкости в этом опыте.

Формула стокса-

Fтр = 6Пnrv где-r-радиус шарика, v-скорость шарика.

Ход работы-

1. цилиндр наполняем глицерином.(цилиндр с 2-мя кольцевыми метками

2. отмечаем высоту

3. берем стальные шарики, измеряем их диаметр.

4. в жидкость опускаем шарики и в определенном промежутке засекаем время.

5. данные вносим в табл

6. определяем вязкость жидкости.

n= d2tg(пл.ш-пл.ж)/18l

где.пл.ж-плотность жидкости

пл.ш-плотность шарика

n-вязкость(ню)

d-диаметр шарика

t-время

g=9,8

l-высота

11.подробно объяснить ход работы по определению коэффициента вязкости жидкости методом оствальда, дать формулу для вычисления вязкости в этом опыте.

Ход работы:

1.жидкость известной концентрации наливаем в вискозиметр и с помощью шприца поднимаем столб жидкости выше верхнего резервуара.

2.с помощью секундомера засекаем время вытекания жидкости из верхнего резервуара.

3.Проводим этот опыт 3 раза с жидкостями с концентрацией 50%, 25%, 12% и неизв. концентрацией.

4.строим график зависимости вязкости и по нему примерно определяем неизв. Концентрацию.(по оси У-вязкость, по оси Х-концентрация)

Формула вязкости по оствальду.

Vисл/Vводы =Тисл\Тводы

Где-Vисл- вязкость исследуемой жидкости

Т-время вытекания жидкости

Vисл=А*Тисл

12.условия применимости закона Пуазейля. Формула Пуазэйля. Гидравлическое сопротивление.

Условия применения

Формулой Пуазейля пользуются при расчетах показателей транспортировки жидкостей и газов в трубопроводах различного назначения. Ламинарный режим работы нефте- и газопроводов является наиболее выгодным в энергетическом отношении. Так, в частности, коэффициент трения при ламинарном режиме практически не зависит от шероховатости внутренней поверхности трубы (гладкие трубы).

Формула Пуазейля:

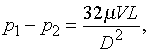формула Пуазейля для перепада давления, необходимого для поддержания вязкого течения в малой трубке постоянного диаметра D длиной L:

Гидравлическое сопротивление -сопротивление движению жидкости, приводящее к потере механической энергии потока (потери напора, гидравлические потери). Гидравлические сопротивления подразделяют на линейные сопротивления (по длине прямолинейного пути), обусловленные вязкостью жидкости, и местные сопротивления возникающие в местах изменения диаметра или направления к скорости потока (в задвижках, вентилях, коленях, тоойниках, диафрагмах и т. д.)

13.последовательное соединение трубок, 2 условия. Вывести формулу для гидравлического соединения последовательно соединенных трубок.

Последовательное соединение. Возьмем несколько труб различной длины, разного диаметра и содержащих разные местные сопротивления, и соединим их последовательно.

П ри подаче жидкости по такому составному трубопроводу от точки М к точке N расход жидкости Q во всех последовательно соединенных трубах 1, 2 и 3 будет одинаков, а полная потеря напора между точками М и N равна сумме потерь напора во всех последовательно соединенных трубах. Таким образом, для последовательного соединения имеем следующие основные уравнения:

Q₁ = Q₂ = Q₃ = Q

Σ^h_M-N ⁼ Σ^h₁ ⁺ Σ^h₂ ⁺ Σ^h₃

Эти уравнения определяют правила построения характеристик последовательного соединения труб (рис. 6.3, б). Если известны характеристики каждого трубопровода, то по ним можно построить характеристику всего последовательного соединения M-N. Для этого нужно сложить ординаты всех трех кривых.

Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Открыт в 1660 году английским учёным Робертом Гуком (Хуком) (англ. Robert Hooke). Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности. В словесной форме закон звучит следующим образом: Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации Для тонкого растяжимого стержня закон Гука имеет вид:

Здесь F — сила натяжения стержня, Δl — абсолютное удлинение (сжатие) стержня, а k называется коэффициентом упругости (или жёсткости). Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения S и длины L) явно, записав коэффициент упругости как

Величина E называется Модулем упругости первого рода или модулем Юнга и является механической характеристикой материала. Если ввести относительное удлинение

и нормальное напряжение в поперечном сечении

то закон Гука в относительных единицах запишется как

В такой форме он справедлив для любых малых объёмов вещества. Также при расчёте прямых стержней применяют запись закона Гука в относительной форме

Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.

Электричество и магнетизм. Основы мед. электроники

1.Закон Ома для переменного тока

Если ток является синусоидальным с циклической частотой ω, а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:

где:

U = U0eiωt — напряжение или разность потенциалов,

I — сила тока,

Z = Re−iδ — комплексное сопротивление (импеданс),

R = (Ra2 + Rr2)1/2 — полное сопротивление,

Rr = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),

Rа — активное (омическое) сопротивление, не зависящее от частоты,

δ = − arctg (Rr/Ra) — сдвиг фаз между напряжением и силой тока.

Реактивное сопротивление – это сопротивление катушек индуктивности (дросселей) и конденсаторов. Величина реактивного сопротивления уже зависит от частоты тока. Так на постоянном токе реактивное сопротивление конденсатора устремляется к бесконечности, а дросселя наоборот – к нулю (без учета активной составляющей сопротивления провода).

С изменением частоты тока электрическое сопротивление конденсатора изменяется, по закону:

Xc = 1/2pfC2

где Xc – сопротивление, Ом; f – частота, Гц; С – емкость, Ф.

Электрическое сопротивление конденсатора переменному току можно измерить. Зная сопротивление и частоту тока, легко по формуле вычислить емкость. Кроме того, если в электрической цепи стоит конденсатор происходит сдвиг фаз напряжения и тока. Причем ток опережает напряжение на величину 90°.

Реактивное сопротивление катушки индуктивности с увеличением частоты возрастает:

XL = 2pfL

где XL – сопротивление катушки, Ом; f – частота, Гц; L – индуктивность, Гн.

Индуктивность дросселя легко вычисляется по известному сопротивлению и заданной частоте тока. При этом фазы напряжения и тока на катушке индуктивности сдвигаются относительно друг друга, и теперь ток отстает от напряжения на 90°.

Для измерения реактивного сопротивления емкости и индуктивности потребуется, прежде всего, переменный ток синусоидальной формы. С задачей программного генератора с легкостью может справиться звуковая плата компьютера. Другая проблема – определение величины электрического сопротивления измеряемого элемента. Но оказывается и эту задачу можно решить программным путем, с помощью той же звуковой платы, не прибегая к специальным аналого-цифровым преобразователям

2. Импеданс - это  полное сопротивление в цепи переменного тока, т.е. его активная и реактивная составляющие. Обозначают импеданс буквой – Z

В общем случае мгновенное значение силы тока i определяется по формуле ,

где j - разность (сдвиг) фаз между колебаниями тока и напряжения, I_m – амплитуда силы тока.

• В проводнике с активным сопротивлением (резисторе) колебания силы тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока определяется равенствомгдеR – (активное) сопротивление резистора.

• В катушке индуктивности колебания силы тока отстают от колебаний напряжения на угол j=p/2. Амплитуда силы тока в катушке равна 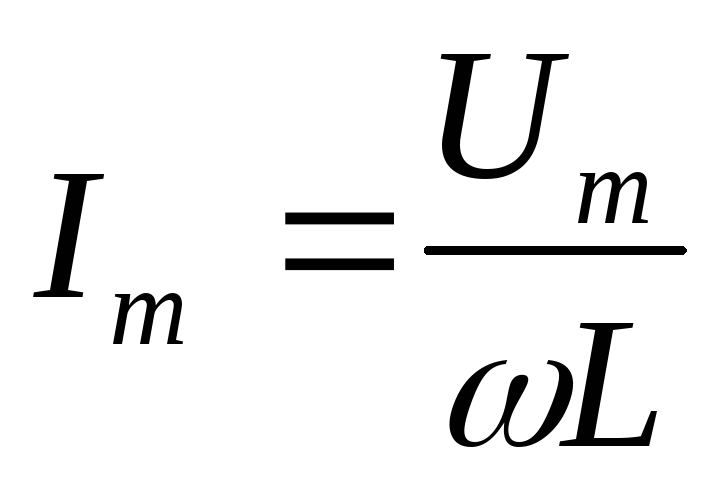. ВеличинуX_L =wL = 2pfL называют индуктивным сопротивлением.

• На конденсаторе колебания силы тока опережают колебания напряжение на угол j=p/2. Амплитуда силы тока равна: . Величину 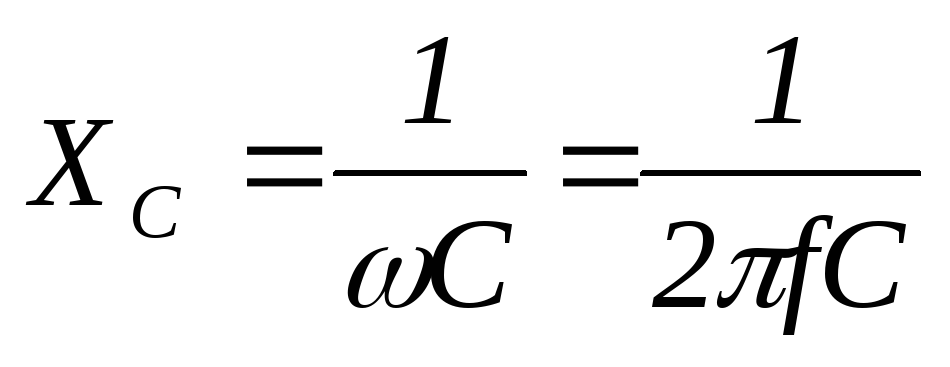называютемкостным сопротивлением.

Полное сопротивление цепи равно:

а сдвиг фаз между током и напряжением

Разность X = (X_L - X_C) называется реактивным сопротивлением цепи. R называется активным сопротивлением цепи.

Для построения зависимости от частотыw вначале строятся зависимости (рис.2,3,4)

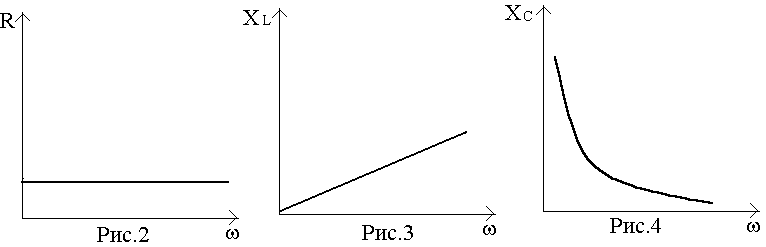
Затем графики зависимостей представляем на одном рисунке (рис.5). Указанные кривые пересекаются. Точка пересечения этих графиков означает, что при определенном значении частоты источника переменного

тока w емкостное сопротивление конденсатора и индуктивное сопротивления катушки индуктивности равны, т. е. XC=XL или и тогда.

3. Электрический диполь-это совокупность двух равных по величине разноимённых точечных зарядов q, расположенныхна некотором расстоянии l друг от друга, малом по сравнению с расстоянием до рассматриваемой точки поля. Электрическими диполями являются полярные молекулы, например молекула воды, совокупность диполей представляют мембраны клеток.

Для фиксированных угловых координат (то есть на луче, идущем из центра электрического диполя на бесконечность) напряжённость статического[прим 4] электрического поля диполя или в целом нейтральной системы зарядов, имеющей ненулевой дипольный момент,[прим 5] на больших расстояниях r асимптотически приближается к виду r−3, электрический потенциал — к r−2. Таким образом, статическое поле диполя убывает на больших расстояниях быстрее, чем поле простого заряда (но медленнее, чем поле любого более старшего мультиполя).

Напряжённость электрического поля и электрический потенциал неподвижного или медленно движущегося диполя (или в целом нейтральной системы зарядов, имеющей ненулевой дипольный момент) с электрическим дипольным моментом на больших расстояниях в главном приближении выражается как:

в СГСЭ:

в СИ: где — единичный вектор из центра диполя в направлении точки измерения, а точкой обозначено скалярное произведение.

Достаточно просты выражения (в том же приближении, тождественно совпадающие с формулами, приведенными выше) для продольной (вдоль радус-вектора, проведенного от диполя в данную точку) и поперечной компонент напряженности электрического поля:где θ — угол между направлением вектора дипольного момента и радиус-вектором в точку наблюдения (формулы приведены в системе СГС; в СИ аналогичные формулы отличаются только множителем ). Третья компонента напряженности электрического поля — ортогональная плоскости, в которой лежат вектор дипольного момента и радиус-вектор, — всегда равна нулю.

4.Токовый монополь- единичный источник электрического потенциала. Вывод формулы потенциала поля токового монополя в бесконечно проводящей среде:

j= - 1/π * dφ( «фи»)/ dr

Где j- плотность электрического поля Р(пи) –удельное сопротивление среды, r- расстояние до униполя.

Токовый диполь- это совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга.

«Электробезопасность медицинской аппаратуры»

Современная больница, клиника, любое другое лечебно-профилактическое учреждение располагают большим количеством разнообразных медицинских приборов, аппаратов, вспомогательных устройств, в которых в том или ином виде используется электрическая энергия. Электромедицинская аппаратура, насчитывающая более 5000 наименований, находит применение для диагностики, лечения, обслуживания пациента, при лабораторных исследованиях, сборе и обработке информации, иначе говоря, на всех стадиях лечебного процесса.

Использованию электрической энергии сопутствует опасность поражения электрическим током. Эта опасность для современного человека имеется практически повсюду: и дома, и на работе, и при пользовании средствами транспорта.

Каковы же специфические условия, которые требуют особых мер по защите пациента и медицинского персонала от поражения электрическим током?

Прежде всего, следует учесть, что у больного защитные силы организма подорваны, поэтому случайное воздействие электрическим током может иметь для больного, особенно страдающего заболеванием сердца, более тяжелые последствия, чем для здорового человека.

Пациент во многих случаях не может нормально реагировать на действие электрического тока, чтобы уменьшить возникшую опасность. Он может быть парализован, находиться под наркозом, быть без сознания, наконец, он может быть привязан к операционному столу или кровати.

В повседневной жизни, на производстве - всюду принимаются все меры для того, чтобы отделить человека от возможных источников электрического тока, от любых электрических цепей. В противоположность этому пациента намеренно подвергают действию тока, его включают непосредственно в цепь постоянного низкочастотного или высокочастотного тока.

Кожный покров является естественной защитой человека от действия электрического тока. В медицинском учреждении кожу пациента обрабатывают обезжиривающими, дезинфицирующими и другими растворами. Увлажненная кожа полностью теряет свои достаточно высокие изолирующие свойства. В полости тела вводят различного рода электроды, датчики, осветительные устройства, во время операции кожный покров механически разрушается, обнажаются внутренние органы. Наиболее опасный случай вмешательства в организм человека - введение электродов, катетеров непосредственно в полость или мышцу сердца.

В процесс лечения или обследования к больному нередко подключаются не один, а несколько аппаратов. Так, например, на операционном столе к пациенту могут быть присоединены электроды высокочастотного электрохирургического аппарата, электроды электрокардиографа, наркозный аппарат, электроотсасыватель, датчики температуры, давления, аппарат сердце - легкие и другая аппаратура. Естественно, что, находясь в центре сплетения проводов, электродов, датчиков, пациент подвергается различным опасностям поражения током, предусмотреть которые заранее весьма сложно.

Немало возможностей и косвенного влияния электрической энергии на безопасность пациента. Различного происхождения электрические, магнитные и электромагнитные поля оказывают мешающее действие чувствительной измерительной аппаратуре, осложняя правильное диагностирование. Действие помех на электрокардиостимуляторы, устройства автоматики аппаратов для искусственного дыхания и другую аппаратуру для замещения либо поддержания функций органов организма может иметь катастрофические последствия. Так же чрезвычайно опасно прекращение подачи напряжения питания на замещающую аппаратуру либо на источник освещения при ответственных оперативных вмешательствах.

Используемая в медицинских учреждениях аппаратура находится в очень тяжелых условиях эксплуатации. Многие аппараты постоянно передвигают, переносят из палаты в палату, при этом возможны толчки, удары их. Сетевые шнуры и кабели подвергаются натяжению, закручиваясь вокруг окружающих предметов, они постоянно оказываются под ногами пациентов и персонала. Приходится считаться с возможностью воздействия на аппараты различных жидкостей (крови, мочи, медикаментов).

Тяжелые условия эксплуатации аппаратуры приводят к частым нарушениям ее, выходу из строя.

Разнообразие и сложность обстоятельств, в которых оказывается больной в медицинском учреждении, приводит к тому, что для обеспечения его электробезопасности недостаточно отдельных изолированных мер защиты в аппарате или в электрооборудовании здания. Только комплекс согласованных между собой защитных средств, принятых при создании аппарата, а также при оборудовании медицинского учреждения, может обеспечить необходимый уровень электробезопасности. При этом обязательным условием является достаточная квалификация специально обученного медицинского персонала, а также технических работников, обеспечивающих регулярный контроль и ремонт аппаратуры и электрооборудования здания.

электробезопасность аппаратура порог тока

Вопрос 10

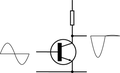
Устройство и принцип действия

УНЧ с обратной связью. Типичная схема

[править]Структура усилителя

Усилитель представляет собой в общем случае последовательность каскадов усиления (бывают и однокаскадные усилители), соединённых между собой прямыми связями

В большинстве усилителей кроме прямых присутствуют и обратные связи (межкаскадные и внутрикаскадные). Отрицательные обратные связи позволяют улучшить стабильность работы усилителя и уменьшить частотные и нелинейные искажения сигнала. В некоторых случаях обратные связи включают термозависимые элементы (термисторы, позисторы) — для температурной стабилизации усилителя или частотнозависимые элементы — для выравнивания частотной характеристики

Некоторые усилители (обычно УВЧ радиоприёмных и радиопередающих устройств) оснащены системами автоматической регулировки усиления (АРУ) или автоматической регулировки мощности (АРМ). Эти системы позволяют поддерживать приблизительно постоянный средний уровень выходного сигнала при изменениях уровня входного сигнала.

Между каскадами усилителя, а также в его входных и выходных цепях, могут включаться аттенюаторы или потенциометры — для регулировки усиления, фильтры — для формирования заданной частотной характеристики и различные функциональные устройства — нелинейные и др.

Как и в любом активном устройстве в усилителе также присутствует источник первичного или вторичного электропитания (если усилитель представляет собой самостоятельное устройство) или цепи, через которые питающие напряжения подаются с отдельного блока питания.

[править]Каскады усиления

Каскад усиления — ступень усилителя, содержащая один или несколько усилительных элементов, цепи нагрузки и связи с предыдущими или последующими ступенями.

В качестве усилительных элементов обычно используются электронные лампы или транзисторы (биполярные, полевые), иногда, в некоторых специальных случаях, могут применяться идвухполюсники, например, туннельные диоды (используется свойство отрицательного сопротивления) и др. Полупроводниковые усилительные элементы (а иногда и вакуумные) могут быть не только дискретными (отдельными) но и интегральными (в составе микросхем), часто в одной микросхеме реализуется полностью законченный усилитель.

В зависимости от способа включения усилительного элемента различаются каскады с общей базой, общим эмиттером, общим коллектором (эмиттерный повторитель) (у биполярного транзистора), с общим затвором, общим истоком, общим стоком (истоковый повторитель) (у полевого транзистора) и с общей сеткой, общим катодом, общим анодом (у ламп)

Каскад с общим эмиттером (истоком, катодом) — наиболее распространённый способ включения, позволяет усиливать сигнал по току и напряжению одновременно, сдвигает фазу на 180°, то есть является инвертирующим.

Каскад с общей базой (затвором, сеткой) — усиливает только по напряжению, применяется редко, является наиболее высокочастотным, фазу не сдвигает.

Каскад с общим коллектором (стоком, анодом) — называется также повторителем (эмиттерным, истоковым, катодным), усиливает ток, оставляя напряжение сигнала равным исходному. Применяется в качестве буферного усилителя. Важными свойствами повторителя являются его высокое входное и низкое выходное сопротивления, фазу не сдвигает.

Каскад с распределенной нагрузкой — каскад, занимающий промежуточное положение между схемой включения с общим эмиттером и общим коллектором. Как вариант каскада с распределенной нагрузкой, выходной каскад усилителя мощности «двухподвес». Важными свойствами являются задаваемый элементами схемы фиксированный коэффициент усиления по напряжению и низкие нелинейные искажения. Выходной сигнал дифференциальный.

Каскодный усилитель — усилитель, содержащий два активных элемента, первый из которых включен по схеме с общим эмиттером (истоком, катодом), а второй — по схеме с общей базой (затвором, сеткой).Каскодный усилитель обладает повышенной стабильностью работы и малой входной ёмкостью. Название усилителя произошло от словосочетания «КАСКад через катОД» (англ. CASCadetocathODE)^[1]

Каскады усиления могут быть однотактными и двухтактными.

Однотактный усилитель — усилитель, в котором входной сигнал поступает во входную цепь одного усилительного элемента или одной группы элементов, соединённых параллельно.

Двухтактный усилитель — усилитель, в котором входной сигнал поступает одновременно во входные цепи двух усилительных элементов или двух групп усилительных элементов, соединённых параллельно, со сдвигом по фазе на 180°.

[править]Режимы (классы) мощных усилительных каскадов

Особенности выбора режима мощных каскадов связаны с задачами повышения экономичности питания и уменьшения нелинейных искажений.

В зависимости от способа размещения начальной рабочей точки усилительного прибора на статических и динамических характеристиках различают следующие режимы усиления

Режим A

 

Режим B

 

Режим B, двухтактный каскад

 

Режим C

 

Углы отсечки полуволны сигнала в различных режимах