4. Параметры нормального распределения

Анализируя (11) можно сделать вывод, что нормальное распределение определяется двумя числовыми характеристиками – математическим ожиданием и дисперсией генеральной совокупности. Для нормального распределения математическое ожидание является наиболее вероятным значением случайной переменной x, а генеральная дисперсия характеризует, насколько «далеко» частные наблюдения величины x могут располагаться относительно M{x}. Внутри интервала ±{x} находится 68,3% всей площади фигуры, ограниченной осью абсцисс и кривой {x}, в интервале ±2{x} – 95,75%. Такое же соотношение при достаточно большом количестве опытов наблюдается для элементов выборки, находящихся внутри и за пределами указанных интервалов.

Для ограниченной выборки оценкой M{x} является 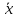, а оценкой ²{x} - S²{x}, где S²{x} – выборочная дисперсия, определяемая выражением

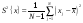1212\* MERGEFORMAT ()

При этом возникает ошибка расчёта значений функции {x}. Поскольку однозначно определить значения M{x} и ²{x} можно лишь при бесконечном числе опытов, то применяют методы интервального оценивания параметров генеральной совокупности, позволяющие определить доверительные интервалы наблюдения математического ожидания и генеральной дисперсии случайной величины.

Определение доверительного интервала наблюдения математического ожидания случайной переменной x осуществляется при помощи статистики Стьюдента или t-критерия. С этой целью задаются необходимым уровнем значимости q и определяют значение квантиля t_КР{1-q/2; N-1} распределения Стьюдента для данной вероятности и текущего объёма выборки N. Границы доверительного интервала наблюдения математического ожидания случайной переменной x определяют по выражению

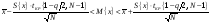1313\* MERGEFORMAT ()

Для определения доверительного интервала наблюдения генеральной дисперсии пользуются статистикой Пирсона (²-критерием). При этом задаются необходимым уровнем значимости q и определяют значения квантилей ²_КР{1-q/2; N-1} и ²_КР{q/2; N-1} распределения Пирсона для данной вероятности и текущего объёма выборки N. Границы доверительного интервала наблюдения генеральной дисперсии определяют по выражению

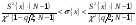1414\* MERGEFORMAT ()

5. Проверка гипотезы о согласовании выборочного эмпирического распределения с гипотетически нормальным распределением

При сопоставлении значений функци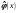й и 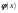для случайной величины x, распределённой нормально, при одном и том же значении аргумента, возникают ошибки 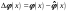. Эти ошибкой могут быть обусловлены либо ошибками определения величин M{x} и ²{x}, либо тем, что закон распределения случайной величины отличен от закона Гаусса. Идея сравнения эмпирического распределения 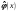с идеальным нормальным распределением 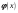, определённым величинами M{x} = и ²{x} = S²{x}, лежит в основе доказательства гипотезы о том, что случайная переменная подчиняется нормальному закону распределения.

Для проверки гипотезы о согласованности эмпирического выборочного распределения с гипотетическим нормальным распределением применяется статистика, которая приближённо распределена по ²-закону Пирсона

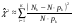1515\* MERGEFORMAT ()

с числом степеней свободы f = K – l – 1, где K – число интервалов ряда распределения, определённое по (9), l  – число параметров гипотетического распределения, которые надо определить по данным выборки (для нормального распределения l = 2). Здесь N_k – число элементов выборки, попавшее в k-ый интервал, а p_k – вероятность попадания случайной величины x в k-ый интервал при условии, что x распределена нормально.

Для проверки нуль-гипотезы о соответствии выборочного распределения нормальному закону Гаусса вычисляют эмпирическое значение статистики по (15) и сравнивают его с критическим ²_КР{q; f }, которое выбирают из таблиц ²-распределения для числа степеней свободы f  и выбранного уровня значимости q. Если выполняется условие

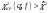1616\* MERGEFORMAT ()

то гипотеза принимается, эмпирическое распределение считается нормальным.

Критерием Пирсона рекомендуется пользоваться при N > 50. При меньших объёмах выборки можно воспользоваться критерием согласия:

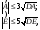1717\* MERGEFORMAT ()

где 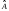, 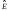– соответственно асимметрия и эксцесс эмпирического распределения, а DA и DE – дисперсии данных величин. Величины 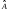, , 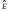DA и DE определяются по выражениям

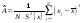1818\* MERGEFORMAT ()

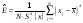1919\* MERGEFORMAT ()

2020\* MERGEFORMAT ()

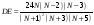2121\* MERGEFORMAT ()

При выполнении условий (17) гипотеза о соответствии выборочного распределения нормальному закону Гаусса принимается.