1. Теоретические сведения

1. Основные термины и определения

Ход изложения материала в данных методических указаниях учитывает то, что согласно программе подготовки инженеров по специальности «Промышленная электроника» на третьем курсе студенты должны иметь представление о предмете теории вероятностей и математической статистики. Однако для лучшего взаимопонимания необходимо дать некоторые определения из теории вероятностей и математической статистики.

Теория вероятностей – математическая наука, изучающая закономерности в массовых однородных случайных явлениях, т.е. таких явлениях природы и общества, которые при неоднократных наблюдениях или измерениях, казалось бы, в однородных условиях дают различающиеся результаты и которые невозможно заранее предсказать с абсолютной точностью.

Математическая статистика – наука о математических методах систематизации, обработки, анализа и использования статистических опытных данных для научных и практических выводов, для выявления объективных закономерностей.

Опыт – это воспроизведение или наблюдение какого-либо явления при определённом комплексе условий в целях испытания или исследования. В случае наблюдения явления опыт называется пассивным, в случае воспроизведения – активным.

Событие – это качественная характеристика опыта, заключающаяся в свершении или отсутствии какого-либо желаемого факта в результате опыта.

События имеют свою классификацию.

По степени достоверности события подразделяют: а) на достоверные (происходящие всегда в любом опыте); б) на невозможные; в) на случайные (промежуточные между достоверными и невозможными).

Случайные события, в свою очередь, также имеют классификацию.

По признаку совместимости случайные события подразделяют: а) на совместимые и б) несовместимые. Например, пусть событие – появление короля при вытягивании карты из колоды, событие – появление бубновой карты, а событие - появление карты трефовой масти. Тогда событие и – совместные, так как возможно появление бубнового короля. Аналогично совместны события и . События же и 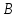– несовместные, так как карт бубновой и трефовой мастей одновременно не существует (имеется ввиду стандартная колода карт без учёта джокера).

По степени возможности случайные события подразделяют: а) на равновозможные и б) на неравновозможные. Например, при бросании игрального кубика, появление любого из очков, от 1 до 6, должно быть равновозможным. Это можно доказать практически при большом числе опытов.

Рассматривают также противоположные события: например событие  – попадание пули в мишень, противоположно событию – промаху.

Результат наблюдения (или просто наблюдение), если он получен в виде некоторого числа является количественной характеристикой опыта, выраженная числовым результатом измерения.

Случайная величина ­­­– есть такая величина, конкретное значение которой в результате опыта невозможно заранее точно предсказать. Непрерывная случайная величина – случайная величина, которая может принимать любые частные значения в широком диапазоне. Дискретная случайная величина может принимать только определённое количество фиксированных значений , называемые её вариантами или дискретами. При этом совокупность К значений случайной величины x называют её спектром. Дискреты случайной величины на числовой оси могут располагаться неравномерно. Непрерывно-дискретная случайная величина – случайная величина, которая на отдельных участках числовой оси дискретна, а на остальных – непрерывна.

Статистической совокупностью называют совокупность всех частных значений случайной переменной, которые либо получены, либо могут быть получены в результате специальных опытов или текущего учёта.

Генеральная статистическая совокупность содержит все возможные частные значения случайной величины. Выборочная статистическая совокупность (выборка, проба) обычно является лишь небольшой частью генеральной. Элемент статистической совокупности – одно из частных значений x_j случайной величины x в данной статистической совокупности. Объёмом статистической совокупности называется общее количество N её элементов. Для генеральной совокупности обычно . Для выборки всегда .

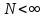Относительная частота ν_k дискретной случайной величины x определяется числом N_k элементов в её k-м варианте x_k к общему объёму N выборки, т.е.

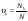11\* MERGEFORMAT ()

Понятие вероятности случайной величины применяется по отношению к генеральной совокупности. Известны три основные определения вероятности:

1. количественная мера «уверенности»;

2. доля, которую данное случайное событие занимает среди всех равновозможных событий;

3. предел относительной частоты, когда .

В данном методическом указании под вероятностью p_k события (появления случайной величины в её k-м варианте) понимается предел относительной частоты ν_k при бесконечном увеличении объёма статистической совокупности

22\* MERGEFORMAT ()

Интервал случайной величины x – это связная область (отрезок) между двумя частными значениями x на её числовой оси, например x_j и x_l, внутрь которой может попасть (или не попасть) некоторое количество элементов выборки x. При этом, если граница включается в интервал – она называется открытой, если исключается из интервала – закрытой, т.е. при условии x_j < x ≤ x_l граница x_j будет открытой, а граница x_l – закрытой.

Плотность вероятности непрерывной случайной величины определяется как вероятность её появления, приходящаяся на некоторый единичный интервал:

33\* MERGEFORMAT ()

Плотность относительной частоты:

44\* MERGEFORMAT ()