1.4. Полный дифференциал функции двух переменных

Полным приращением функции z = f(x, y) в точке называется величина .

Полным дифференциалом функции z = f(x, y)называется величина, вычисляемая по формуле:

.

(1.4)

Формула приближенных вычислений:

.

(1.5)

1.5. Производные сложной функции

Пусть задана сложная функция , , , тогда частные производные можно найти по следующим формулам:

(1.6)

Если , , , тогда может быть вычислена полная производная сложной функции z по аргументу х согласно формуле:

.

(1.7)

В частности, если , где , то производная вычисляется по формуле:

.

(1.8)

1.6. Производные неявной функции

Неявной функцией у аргумента х называется функция, значения которой находятся из уравнения, связывающего и неразрешенного относительно у, т. е.

.

(1.9)

Производная неявной функции находится по следующей формуле:

.

(1.10)

Неявной функцией z аргументов x и y называется функция, значения которой находятся из уравнения, связывающего и неразрешенного относительно z, т. е.

.

(1.11)

Частные производные неявной функции находятся по следующим формулам:

.

(1.12)

1.7. Производная по направлению, градиент

Градиентом функции в точке называется вектор с началом в точке М, имеющий своими координатами значения частных производных функции z в точке М, т. е.

.

(1.13)

Для обозначения градиента часто используют символ . Направление градиента функции в данной точке есть направление наибольшей скорости возрастания функции в этой точке.

Производной функции в точке в направлении вектора называется

.

(1.14)

Если функция дифференцируема, то производная в данном направлении вычисляется по формуле

,

(1.15)

где  - угол между вектором и осью О_х .

Пользуясь определением градиента, формулу (1.15) для производной по направлению можно представить в виде скалярного произведения:

,

(1.16)

где вектор - орт вектора .

Т. е. производная функции по данному направлению равна скалярному произведению градиента функции на единичный вектор этого направления.

Производная в направлении градиента имеет наибольшее значение равное

.

(1.17)

1.8. Касательная плоскость и нормаль к поверхности

Касательной плоскостью к поверхности в данной точке М (точке касания) называется плоскость, в которой лежат касательные в этой точке ко всевозможным кривым, проведенным на данной поверхности через указанную точку.

Нормалью к поверхности называется прямая, перпендикулярная к касательной плоскости в точке касания.

Пусть поверхность задана уравнением ; возьмем на ней точку .

Тогда уравнение касательной плоскости в точке имеет вид:

,

(1.18)

а уравнение нормали имеет вид:

.

(1.19)

Если уравнение поверхности задано в явном виде , то

^{, , .}

1.9. Экстремумы функций двух переменных

Точка называется точкой локального максимума функции , если для всех точек , принадлежащих достаточно малой окрестности точки , выполняется неравенство . Значение функции в точке максимума называется локальным максимумом функции.

Точка называется точкой локального минимума функции , если для всех точек , принадлежащих достаточно малой окрестности точки , выполняется неравенство . Значение функции в точке минимума называется локальным минимумом функции.

Точки максимума и минимума функции называются точками экстремума функции, а значения функции в этих точках называются экстремумами функции.

Необходимое условие существования экстремума функции двух переменных: если функция достигает экстремума в точке , то ее частные производные первого порядка в этой точке равны нулю, т. е.

.

(1.20)

Точки, в которых частные производные равны нулю, называются стационарными точками. Не всякая стационарная точка является точкой экстремума.

Достаточное условие существования экстремума функции двух переменных: пусть - стационарная точка функции .

Обозначим:

;  ;

(1.21)

и составим соотношение

.

(1.22)

Тогда:

1) если , то значение функции - есть экстремум, причем это максимум, если и минимум, если ;

2) если , то значение функции экстремумом не является;

3) если , то требуется дальнейшее исследование.
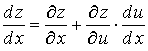