Правило Лопиталя. Раскрытие неопределенностей вида ....... С помощью правила Лопиталя.

Формулы Тейлора и Маклорена. Остаточный член формулы Тейлора в форме Пеано и Лагранжа. Разложения по формуле Тейлора функций ,,,,,в окрестности точки. Вычисление пределов с помощью формулы Тейлора.

• Функция дифференцируема в точке тогда и только тогда, когда у неё существует конечная производная. Более того

• Дифференциал функции (соответственно производная) определяется единственным образом.

• Функция, дифференцируемая в какой-либо точке, непрерывна в ней же, то есть 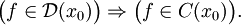Обратное утверждение неверно.

Связь между непрерывностью и дифференцируемостью функции

Теорема (необходимое условие дифференцируемости функции). Если функция дифференцируема в точке, то она непрерывна в этой точке.

Доказательство. Пусть функция у=f(x) дифференцируема в точке х0. Дадим в этой точке аргументу приращение Dх. Функция получит приращение Dу. Найдем .

.

Следовательно, у=f(x) непрерывна в точке х0.

Следствие. Если х0 – точка разрыва функции, то в ней функция не дифференцируема.

Теорема Ферма

Если f(x) дифференцируема в точке x0 и принимает в этой точке наибольшее или наименьшее значение для некоторой окрестности точки x0, то f’(x)=0.

Доказательство:

пусть f(x0) – наибольшая.

Теорема(Ролля) Пусть функция y = f(x) непрерывна на отрезке , дифференцируема на интервале (a, b) и f(a) = f(b). Тогда существует числотакое, что f ' (c) = 0.

Доказательство. Так как функция y = f(x) непрерывна на отрезке , то она на этом отрезке достигает своего наибольшего и своего наименьшего значения.

Обозначим

Если M = m, то f(x) = const . Следовательно, f '(x) = 0 для любого , и теорема для данного случая верна. Пусть теперь M≠m. Пусть M>f(a)=f(b). Тогда найдется числотакое, что f(c)=M. При этом имеют место неравенства

Переходя к пределу, получаем

Если при M ≠ m выполнены равенства M = f(a) = f(b), тогда m < f(a) = f(b).

Рассмотрим функцию y = g(x) = - f(x).

Для этой функции и - m > g(a) = g(b).

Из доказанного выше следует, что существует число такое, что g ' (c) = 0. Так как g ' (c) = - f(c), то f(c) = 0 . Теорема доказана.

Теорема Коши(об отношении приращения двух функций)

Пусть функции y = f(x), y = g(x) непрерывны на отрезке и дифференцируемы на интервале (a, b), причем g ' (x) ≠ 0 на (a, b).

Тогда существует число такое, что

Доказательство. Заметим, что g(b) ≠ g(a). (Если g(b) = g(a), то, по теореме Ролля, существует число такое, что g ' (c) = 0.)

Введем обозначение: .

Рассмотрим функцию , которая непрерывна на, дифференцируема на (a, b) и F(a) = F(b) = 0, т.е. функция F удовлетворяет условиям теоремы Ролля.

Следовательно, существует число такое, что F ' (c) = 0.

Так как . Теорема доказана.

Теорема Лагранжа (о конечных приращениях)

Пусть функция y = f(x) непрерывна на отрезке и дифференцируема на интервале (a, b).

Тогда существует число , такое, что.

Доказательство. Необходимо положить g(x) = x и применить теорему Коши. Теорема доказана.

Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть или. Тогда, если существует предел отношения производных этих функций, то существует и предел отношения самих функций f(x)/g(x) при x→а, причем

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

Замечание. Отметим, что формула справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.

ФОРМУЛА ТЕЙЛОРА

Пусть функция y= f(x) задана на (a, b) и x0 Î (a, b). Поставим следующую задачу: найти многочлен P(x), значения которого в окрестности точки x0 приближенно совпадали бы со значениями функции f(x) в соответствующих точках. Тогда можно будет считать, что f(x)≈P(x) и задачу вычисления значений f(x) в окрестности точки x0 можно заменить более легкой задачей вычисления значений P(x).

Пусть искомый многочлен имеет степень n P(x) = Pn(x). Будем искать его в виде (1)

В этом равенстве нам нужно найти коэффициенты .

Для того чтобы этот многочлен был "близок" к функции f(x) потребуем выполнения следующих равенств:

Пусть функция y= f(x) имеет производные до n-ого порядка. Найдем коэффициенты многочлена Pn(x) исходя из условия равенства производных.

Введем обозначение n! = 1·2·3…n, 0! = 1, 1! = 1.

Подставим в (1) x = x0 и найдем , но с другой стороны. Поэтому

Далее найдем производную и вычислимСледовательно,.

Учитывая третье условие и то, что ,

получим , т.е..

Далее . Значит,, т.е..

Очевидно, что и для всех последующих коэффициентов будет верна формула

Подставляя найденные значения коэффициентов в формулу (1), получим искомый многочлен:

Обозначим и назовем эту разность n-ым остаточным членом функции f(x) в точке x0. Отсюдаи, следовательно,если остаточный член будет мал.

Оказывается, что если x0 Î (a, b) при всех x Î (a, b) существует производная f (n+1)(x), то для произвольной точки x Î (a, b) существует точка, лежащая между x0 и x такая, что остаток можно представить в виде:

Это так называемая формула Лагранжа для остаточного члена.

Формула

где x Î (x0, x) называется формулой Тейлора.

Если в этой формуле положить x0 = 0, то она запишется в виде

где x Î ( x0, x). Этот частный случай формулы Тейлора называют формулой МакЛорена.

; ;;; ;;;

(10)

Приложение производной к исследованию функций.

Монотонные функции. Необходимое и достаточное условия монотонности функции. Достаточное условие строгой монотонности.

Экстремум функции. Необходимое условие экстремума. Первое и второе достаточные условия экстремума.

Наибольшее и наименьшее значения функции на отрезке.

Выпуклость, вогнутость графика функции. Достаточное условие выпуклости, вогнутости. Точка перегиба. Достаточное условие существования точки перегиба.

Асимптоты графика функции. Вертикальная асимптота. Наклонная асимптота и критерий ее существования.

Общая схема исследования функции.

Приложение есть правило Лопиталя - Теорема (правило Лопиталя).

Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть или. Тогда, если существует предел отношения производных этих функций, то существует и предел отношения самих функций f(x)/g(x) при x→а, причем

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.

Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательно, либо всегда неположительно. Если в дополнение приращение не равно нулю то функция называется стро́го моното́нной.

Теорема: Критерий постоянства фун.

Функция f(x)=const на промежутке [a,b], тогда, когда f’(x)=0 на интервале (a,b).

Док-во: f(x)=c => f’(x)=c’=0 возьмем x[a,b] и применим т. Лангранжа f(x) [a,b] по т. Лангранжа f(x)-f(a)=f’(c)(x-a); c(a,x); f(x)-f(a)=0; f(x)=f(a) для любого x => f(x)=const.

Теорема: Достаточный признак возрастания функции. Если f’(x)>0, (a,b), то f(x) возрастает на [a,b].

Док-во:

возьмем x1, x2 [a,b]: x1<x2 => f(x2)>f(x1)

применим т. Лангранжа f(x) на [x1,x2]

по этой теореме f(x2)-f(x1)=f’(c)(x2-x1)>0 => f(x2)>f(x1).Замечание: данные условия не являются необходимыми.

Теорема: достаточный признак убывания функции. Если f’(x)<0 на (a,b), то f(x) убывает на [a,b].

Док-во 1: подобно предыдущему.

Док-во 2: g(x)=-f(x),тогда g’(x)=-f’(x)>0

=> g(x) - возрастает => f(x) – убывает.

Несложно показать, что если функция возрастает (убывает) на [a,b], то ее произв. не отрицат.(положит.) на (a,b).

f(x) возрастает: [a,b]=>f’(x)0 (a,b).