Предел функции в точке и на бесконечности. Эквивалентность определений предела функции по Гейне и по Коши. Геометрический смысл предела. Односторонние пределы. Основные теоремы о пределах функции.

Бесконечно малые и бесконечно большие функции. Понятие о неопределенностях. Раскрытие простейших неопределенностей. Первый и второй замечательные пределы. Основные эквивалентности. Функции, эквивалентные функциям в окрестности .

Числовой функцией называется соответствие, которое каждому числу х из некоторого заданного множества сопоставляет единственное число y.

СПОСОБЫ ЗАДАНИЯ ФУНКЦИЙ

1. Аналитический способ: функция задается с помощью

математической формулы.

2. Табличный способ: функция задается с помощью таблицы.

3. Описательный способ: функция задается словесным описанием

4. Графический способ: функция задается с помощью графика

5. Пределы на бесконечности

Пределы функции на бесконечности

Элементарные функции:

1) степенная функция y=xⁿ

2) показательная функция y=a^x

3) логарифмическая функция y=log_ax

4) тригонометрические функции y=sin x, y=cos x, y=tg x, y=ctg x

5) обратные тригонометрические функции y=arcsin x, y=arccos x, y=arctg x, y=arcctg x.

ПустьиТогда система множеств

является фильтром и обозначается или Пределназывается пределом функции f при x стремящемся к бесконечности.

Опр.1. (по Коши). Пусть задана функция y=f(x): X à Y и точка a является предельной для множества X. Число A называется пределом функции y=f(x) в точке a, если для любого ε > 0 можно указать такое δ > 0, что для всех xX, удовлетворяющим неравенствам 0 < |x-a| < δ, выполняется |f(x) – A| < ε.

Опр.2.(по Гейне). Число A называется пределом функции y=f(x) в точке a, если для любой последовательности {x_n}ε X, x_n≠a nN, сходящийся к a, последовательность значений функции {f(x_n)} сходится к числу A.

Теорема. Определение предела функции по Коши и по Гейне эквиваленты.

Доказательство. Пусть A=lim f(x) – предел функции y=f(x) по Коши и {x_n} X, x_na nN – последовательность, сходящаяся к a, x_n à a.

По данному ε > 0 найдем δ > 0 такое, что при 0 < |x-a| < δ, xX имеем |f(x) – A| < ε, а по этому δ найдем номер n_δ =n(δ) такой, что при n>n_δ имеем 0 < |x_n-a| < δ

Но тогда |f(x_n) – A| < ε, т.е. доказано, что f(x_n)à A.

Пусть теперь число A есть теперь предел функции по Гейне, но A не является пределом по Коши. Тогда найдется ε_o > 0 такое, что для всех nN существуют x_nX, 0 < |x_n-a| < 1/n, для которых |f(x_n)-A| >= ε_o. Это означает, что найдена последовательность {x_n} X, x_n≠a nN, x_n à a такая, что последовательность {f(x_n)} не сходится к A.

Геометрический смысл предела lim f(x) функции в точке х₀ таков: если аргументы х будут взяты в ε-окрестности точки х₀, то соответствующие значения останутся в ε-окрестности точки .

Функции могут быть заданы на интервалах, примыкающих к точке x0 разными формулами, либо не определены на одном из интервалов. Для исследования поведения таких функций удобным является понятие левосторонних и правосторонних пределов.

Пусть функция f определена на интервале (a, x0 ). Число A называется пределом функции f слева

в точке x0 если0 0 x ( a, x0 ) , x0 - x x0 : | f ( x ) - A |

Предел функции f справа в точке x0 определяется аналогично.

Бесконечно малые функции обладают следующими свойствами:

1) Алгебраическая сумма любого конечного числа бесконечно малых в некоторой точке функций есть функция, бесконечно малая в той же точке.

2) Произведение любого конечного числа бесконечно малых в некоторой точке функций есть функция, бесконечно малая в той же точке.

3) Произведение бесконечно малой в некоторой точке функции на функцию ограниченную есть функция, бесконечно малая в той же точке.

Бесконечно малые в некоторой точке х0 функции a (x) и b (x) называются бесконечно малыми одного порядка,

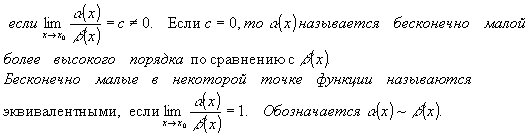
Нарушение ограничений, накладываемых на функции при вычислении их пределов, приводит к неопределенностям

Элементарными приемами раскрытия неопределенностей являются:

1. сокращение на множитель, создающий неопределенность

2. деление числителя и знаменателя на старшую степень аргумента (для отношения многочленов при )

3. применение эквивалентных бесконечно малых и бесконечно больших

4. использование двух замечательных пределов:

Первый замечательный предел

Второй замечательный предел

Функции f(x) и g(x) называются эквивалентными при x→ a, если f(x): f(x) = f (x)g(x), где limx→ af (x) = 1.

Иначе говоря функции эквивалентны при x→ a, если предел их отношения при x→ a равен единице. Справедливы следующие соотношения, их еще называют асимптотическими равенствами:

sin x ~ x, x → 0

tg x ~ x, x → 0, arcsin x ~ x, x ® 0, arctg x~ x, x ® 0

e^x-1~ x, x→ 0

ln (1+x)~ x, x→ 0

^m-1~ mx, x→ 0

(6)

Непрерывность функции. Непрерывность элементарных функций. Арифметические операции над непрерывными функциями. Непрерывность сложной функции. Формулировка теорем Больцано-Коши и Вейерштрасса.

Разрывные функции. Классификация точек разрыва. Примеры.

Функция f(x) называется непрерывной в точке a, если

" U(f(a)) $ U(a) (f(U(a))М U(f(a))).

Непрерывность сложной функции

Теорема 2. Если функция u(x) непрерывна в точке х0, а функция f(u) непрерывна в соответствующей точке u0 = f(x0), то сложная функция f(u(x)) непрерывна в точке х0.

Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 59.

Все элементарные функции непрерывны в каждой точке их областей определения.

Теорема Вейерштрасса

Пусть f — непрерывная функция, определённая на отрезке [a,b]. Тогда для любого существует такой многочлен p с вещественными коэффициентами, что для любого x из выполнено условие

Теорема Больцано — Коши

Пусть дана непрерывная функция на отрезке Пусть такжеи без ограничения общности предположим, чтоТогда для любогосуществуеттакое, что f(c) = C.

Точка разрыва - значение аргумента, при котором нарушается непрерывность функции (см. Непрерывная функция). В простейших случаях нарушение непрерывности в некоторой точке а происходит так, что существуют пределы

при стремлении x к а справа и слева, но хотя бы один из этих пределов отличен от f (a). В этом случае а называют Точкой разрыва 1-го рода. Если при этом f (a + 0) = f (a —0), то разрыв называется устранимым, так как функция f (x) становится непрерывной в точке а, если положить f (a)= f(a+0)=f(a-0).

Разрывные функции, функции, имеющие разрыв в некоторых точках (см. Разрыва точка). Обычно у функций, встречающихся в математике, точки разрыва изолированы, но существуют функции, для которых все точки являются точками разрыва, например функция Дирихле: f (x) = 0, если х рационально, и f (x) = 1, если х иррационально. Предел всюду сходящейся последовательности непрерывных функций может быть Р. ф. Такие Р. ф. называются функциями первого класса по Бэру.

(7)

Производная, ее геометрический и физический смысл. Правила дифференцирования (производная суммы, произведения, частного двух функций; производная сложной функции).

Производная тригонометрических функций.

Производная обратной функции. Производная обратных тригонометрических функций.

Производная логарифмической функции.

Понятие о логарифмическом дифференцировании. Производная степенно-показательной функции. Производная степенной функции. Производная показательной функции. Производная гиперболических функций.

Производная функции, заданной параметрически.

Производная неявной функции.

Производной функции f(x) (f'(x0)) в точке x0 называется число, к которому стремится разностное отношение , стремящемся к нулю.

Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке.

Уравнение касательной к графику функции y=f(x) в точке x0 :

Физический смысл производной.

Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:

Логарифмическое дифференцирование

Если требуется найти из уравнения, то можно:

а) логарифмировать обе части уравнения

;

б) дифференцировать обе части полученного равенства, где есть сложная функция от х,

.

в) заменить его выражением через х

Дифференцирование неявных функций

Пусть уравнение определяеткак неявную функцию от х.

а) продифференцируем по х обе части уравнения , получим уравнение первой степени относительно;

б) из полученного уравнения выразим .

Дифференцирование функций, заданных параметрически

Пусть функция задана параметрическими уравнениями ,

Тогда , или

(8)

Дифференциал. Геометрический смысл дифференциала. Применение дифференциала в приближенных вычислениях. Инвариантность формы первого дифференциала. Критерий дифференцируемости функции.

Производные и дифференциалы высших порядков.

Дифференциал (от лат. differentia — разность, различие) в математике, главная линейная часть приращения функции. Если функция y = f (x) одного переменного х имеет при х = х0 производную, то приращение Dy = f (x0 + Dx) - f (x0) функции f (x) можно представить в виде Dy = f' (x0) Dx + R,

где член R бесконечно мал по сравнению с Dх. Первый член dy = f' (x0) Dх в этом разложении и называется дифференциалом функции f (x) в точке x0.

ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ

Пусть имеем функцию y=f(x), где x – независимая переменная. Тогда дифференциал этой функции dy=f'(x)dx также зависит от переменной x, причем от x зависит только первый сомножитель f'(x) , а dx=Δx от x не зависит (приращение в данной точке x можно выбирать независимо от этой точки). Рассматривая dy как функцию x, мы можем найти дифференциал этой функции.

Дифференциал от дифференциала данной функции y=f(x) называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d²y: d(dy)=d²y.

Найдем выражение второго дифференциала. Т.к. dx от x не зависит, то при нахождении производной его можно считать постоянным, поэтому

d²y = d(dy) = d[f '(x)dx)] = [f '(x)dx]'dx = f ''(x)dx·dx = f ''(x)(dx)².

Принято записывать (dx)² = dx². Итак, d²у= f''(x)dx².

Аналогично третьим дифференциалом или дифференциалом третьего порядка функции называется дифференциал от ее второго дифференциала:

d³y=d(d²y)=[f ''(x)dx²]'dx=f '''(x)dx³.

Вообще дифференциалом n-го порядка называется первый дифференциал от дифференциала (n – 1)-го порядка: dⁿ(y)=d(dⁿ-1y)dⁿy = f (n)(x)dxⁿ

Отсюда, пользуясь дифференциалами различных порядков, производную любого порядка можно представить как отношение дифференциалов соответствующего порядка:

ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛА К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ

Пусть нам известно значение функции y0=f(x0) и ее производной y0' = f '(x0) в точке x0. Покажем, как найти значение функции в некоторой близкой точке x.

Как мы уже выяснили приращение функции Δy можно представить в виде суммы Δy=dy+α·Δx, т.е. приращение функции отличается от дифференциала на величину бесконечно малую. Поэтому, пренебрегая при малых Δx вторым слагаемым в приближенных вычислениях, иногда пользуются приближенным равенством Δy≈dy или Δy≈f'(x0)·Δx.

Т.к., по определению, Δy = f(x) – f(x0), то f(x) – f(x0)≈f'(x0)·Δx.

Откуда f(x) ≈ f(x0) + f'(x0)·Δx

Инвариантная форма первого дифференциала.

df(x)=f’(x)dx

Доказательство:

1)

2)

(9)

Основные теоремы о дифференцируемых функциях. Связь между непрерывностью и дифференцируемостью функции. Теорема Ферма. Теоремы Ролля, Лагранжа, Коши и их следствия. Геометрический смысл теорем Ферма, Ролля и Лагранжа.