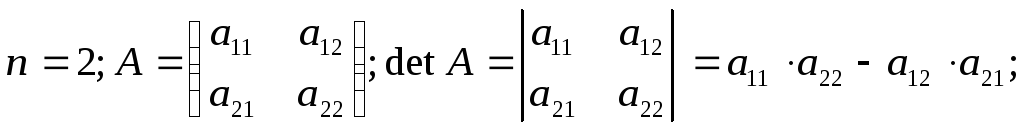(1)Матрицы. Размерность матрицы. Матрица квадратная, треугольная, диагональная, единичная, нулевая, прямоугольная, ступенчатого вида. Элементарные преобразования матриц. Линейная зависимость строк (столбцов) матрицы. Два определения линейной независимости строк и их эквивалентность. Действия с матрицами: сложение, умножение на число, умножение матриц, нахождение обратной матрицы. Свойства этих операций. Определение ранга матрицы. Два способа нахождения ранга матрицы.

Матрица – таблица, содержащая m строк и n столбцов.

Матрица размера n x n называется квадратной матрицей n-го порядка.

Квадратную матрицу размера n x n называют матрицей n-го порядка.

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.

Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной (обозначается буквой E).

Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.

Матрица, все элементы которой равны нулю, называется нулевой (обозначается буквой О).

Матрица ступенчатого вида – матрица, у которой все члены ниже главной диагонали равны нулю.

Элементарные преобразования матриц:

1. Перестановка местами двух параллельных рядов матрицы

2. Умножение всех элементов ряда на число, отличное от нуля

3. Прибавление к элементам одного ряда соответствующих элементов параллельного ряда, умноженных на число.

4. Вычеркивание строки из нулей.

Опр.1.Строки a1; a2; a3;...;an называются линейно независимыми если равенство 1a1+2a2+...+nan=0 возможно только при всех =0.

Опр.2.Строки a1; a2; a3;...;an называются линейно зависимыми если это равенство возможно хотя бы при одном ≠0.

Опр.3.Строки линейно зависимы если одна из строк является линейной комбинацией остальных.

Опр1<=>Опр3

Свойства матриц:

1. A+B=B+A (коммутативный закон сложения)

2. A+(B+C)=(A+B)+C (ассоциативный закон)

3. A+0=A ( закон поглощения нуля)

4. α∙A=A∙α (коммутативный закон умножения)

5. 1∙A=A(закон поглощения единицы)

6. α∙(A+B) =α∙A+ α∙B(дистрибутивный закон)

7. (α+β)∙A= α∙A+ β∙A

8. α∙( βA)= (α β)∙A

Рангом(обозначается r,r(A),rang(A)) матрицы называется наибольший из порядков миноров данной матрицы, отличных от нуля.

<=>

Рангом матрицы называется число линейно независимых строк.

Способы нахождения ранга матрицы:

1. Нахождение наибольшего(базисного) минора матрицы.

2. Приведение к каноническому виду(с помощью элементарных преобразований).

(2) Определители. Вычисление определителей второго порядка. Вычисление определителей высших порядков с помощью теоремы Лапласа. Свойства определителей.

Квадратной матрице A порядка n можно сопоставить число det A, называемое ее определителем, следующим образом:

n=1, A=(a₁); det A= a₁;

1. 

2. 

Теорема Лапласа

Выделим в det A произвольные строки с номерами . Образуем всевозможные миноры k-го порядка с элементами из этих строк. Домножим эти миноры на их алгебраические дополнения в det A. Тогда величина det A равна сумме таких произведений по всем возможным выборкам k элементов.

Свойства определителя:

1. Определитель, содержащий (а) строку из нулей (б) две одинаковые строки (в) две пропорциональные строки – равен нулю

2. Определитель не изменится если к одной строке прибавить другую, умноженную на число.

3. Определитель не меняется при транспонировании => Все свойства, справедливые для строк, справедливы и для столбцов.

4. Постоянный множитель строки\столбца можно вынести за знак определителя.

(3)Системы линейных уравнений. Система n линейных уравнений с k неизвестными. Основные определения: системы совместные, определенные, однородные. Решение систем методом Крамера, методом Гаусса, матричным методом. Исследование систем n уравнений с k неизвестными с помощью метода Гаусса. Элементарные преобразования системы. Совместность системы, ее определенность. Ранг системы линейных уравнений. Два способа вычисления ранга системы линейных уравнений. Теорема Кронекера-Капелли. Неопределенные системы. Однородные системы и их исследование.

Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида

Где числа aij называются коэффициентами системы, числа bij – свободными членами.

Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Совместная называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Если свободные члены всех уравнений равны нулю, то система называется однородной.

Метод Крамера

Метод Гауса

Приведение расширенной матрицы системы к ступенчатому виду с помощью элементарных преобразований и решение соответственной системы.

Матричный метод

Рангом(обозначается r,r(A),rang(A)) матрицы называется наибольший из порядков миноров данной матрицы, отличных от нуля.

<=>

Рангом матрицы называется число линейно независимых строк.

Способы нахождения ранга матрицы:

3. Нахождение наибольшего(базисного) минора матрицы.

4. Приведение к каноническому виду(с помощью элементарных преобразований).

ТЕОРЕМА(1) Кронекера-Капелли.

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.

Теорема(2). Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.

Теорема(3). Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.

Исследование однородных систем:

Однородная система всегда совместна.

Теорема: Для того чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг ее матрицы был меньше числа неизвестных.

Теорема: Для того чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ее определитель был равен нулю.

(4) Линейное пространство. Аксиомы линейного пространства. Линейная зависимость (линейная независимость) системы векторов. Два определения линейно независимой системы векторов и их эквивалентность. Связь между линейной зависимостью (линейной независимостью) системы и подсистемы векторов. Ранг системы векторов. Критерий линейной независимости системы векторов. Базис линейного пространства. Разложение вектора по базису. Координаты вектора в базисе. Размерность линейного пространства.

Множество называется линейным пространством, а его элементы – векторами, если:

1. Задан закон, по которому любым двум элементам (х и у) сопоставляется элемент, называемый их суммой, обозначаемый х+у.

2. Задан закон, по которому элементу х из множества и числу а сопоставляется элемент их множества, называемый произведением х на а и обозначаемый ах.

3. Для любых элементов x, y и z из множества для любых чисел a и b выполнены следующие требования:

• x+y=y+x

• (x+y)+z=x+(y+z)

• х+о=х

• Для каждого элемента х существует такой элемент –х, что х+(-х)=0

• а(х+у)=ах+ау

• (a+b)x=ax+bx

• a(bx)=(ab)

• Произведение любого элемента х на 1 равно х.

a1; a2; a3;...;an - линейно зависимы если их линейная комбинация может принимать любые значения хотя бы при одном ≠0.

<=>

a1; a2; a3;...;an - линейно зависимы если один из них является линейной комбинацией остальных.

a1; a2; a3;...;an – линейно независимы если:

Рангом системы векторов называется максимальное количество линейно независимых векторов системы.

Система векторов называется базисом линейного пространства если:

1. Она линейно независима

2. Любой вектор пространства x линейно выражается через вектора этой системы.

<=>

Система векторов называется базисом линейного пространства если:

1. Она линейно независима

2. Добавление еще одного вектора превращает систему в линейно зависимую.

Коэффициенты линейной комбинации называются компонентами или координатами вектора по базису.

Векторы базиса e_1,…,e_n записываются в строку e=||e_1,…,e_n||, а компоненты ξ¹,… ,ξⁿ вектора х по базису e – в столбец, который называется координатным столбцом вектора. Разложение вектора по базису: х=еξ.

Векторы линейно зависимы тогда и только тогда, когда линейно зависимы их координатные столбцы.

Количество базисных векторов линейного пространства называется размерностью этого пространства.