
1 КУРС (Лекции по оптике и электричеству и магнетизму) / Lektsia_7_pdf109608000
.pdfКрахалев М.Н.
Лекция №7
Индуктивность.
Энергия магнитного поля. Уравнения Максвелла.
Крахалев Михаил Николаевич

КрахалевПланМ.Н. лекции №7
¥Явление самоиндукции. Индуктивность.
¥Индуктивность соленоида. Взаимная индукция.
¥Явления при размыкании и замыкании тока.
¥Энергия магнитного поля.
¥Построение системы уравнений Максвелла. Ток смещения.
¥Интегральная и дифференциальная формы уравнений Максвелла.
¥Граничные условия. Материальные уравнения.
¥Свойства уравнений Максвелла. Электромагнитные волны. Энергия электромагнитной волны. Вектор Пойтинга.
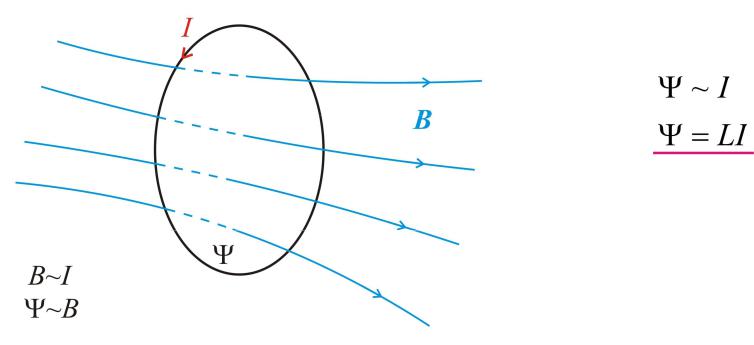
Явление самоиндукции.
Крахалев М.Н.
Коэффициент пропорциональности L между силой тока I и полным магнитным потоком Y называется
индуктивностью контура.
Индуктивность L зависит от геометрии контура (т.е. формы и размеров) и от магнитных свойств (от m) окружающей контур среды. Если контур жесткий и по близости от него нет ферромагнетиков индуктивность L будет постоянной. В присутствии ферромагнетиков (m зависит от I) индуктивность будет зависеть от силы тока I (L является функцией I).
Единица индуктивности в СИ – генри (Гн): 1 Гн - индуктивность такого проводника, у которого при силе тока 1 А возникает полный магнитный поток Y, равный 1 Вб (1 Гн = 1 Вб/1 А).

Явление самоиндукции.
Крахалев М.Н.
Пример:
Индуктивность соленоида
где: l – длинна соленоида, I – ток, протекающий через витки соленоида, n – количество витков на единицу длинны соленоида, N – число витков соленоида, S – площадь поперечного сечения.
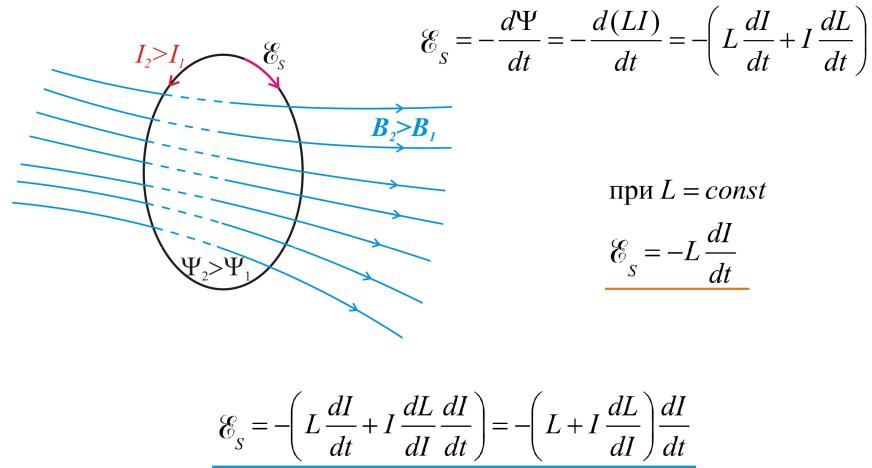
Явление самоиндукции.
Крахалев М.Н.
э.д.с. самоиндукции:
При изменении тока в контуре возникает
э.д.с. самоиндукции, равная:
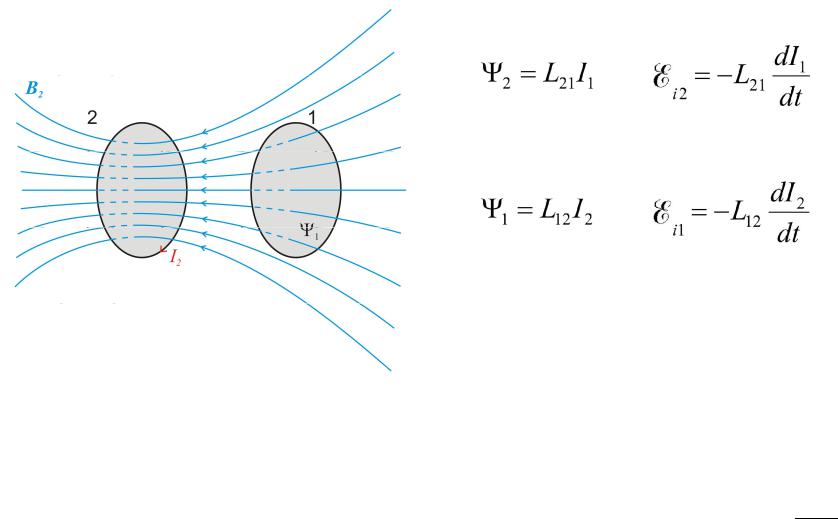
Явление самоиндукции.
Крахалев М.Н.
Взаимная индуктивность:
Контуры 1 и 2 называются связанными (магнитносвязанными). Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией.
Коэффициенты пропорциональности L12 и L21 называются взаимной индуктивностью (коэффициентом взаимной индукции) контуров. L12 = L21. Взаимная индуктивность зависит от геометрии контуров, их взаимного расположения и магнитных свойств среды.
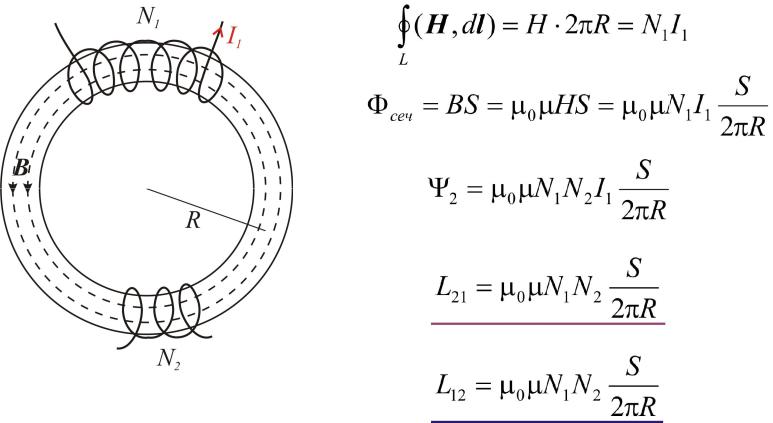
Явление самоиндукции.
Крахалев М.Н.
Пример: взаимная индуктивность двух катушек 1 и 2, состоящих из N1 и N2 витков соответственно,
намотанных на тороидальный сердечник радиуса R.
Явление самоиндукции.
Крахалев М.Н.
Пример: ток при замыкании и размыкании цепи.
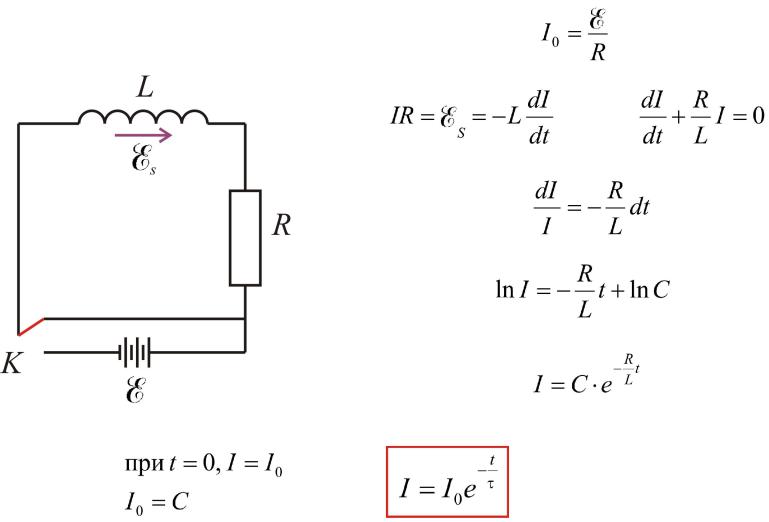
1. Размыкание цепи:
Постоянная времени цепи t –
время, в течении которого сила тока уменьшается в e раз.
Явление самоиндукции.
Крахалев М.Н.
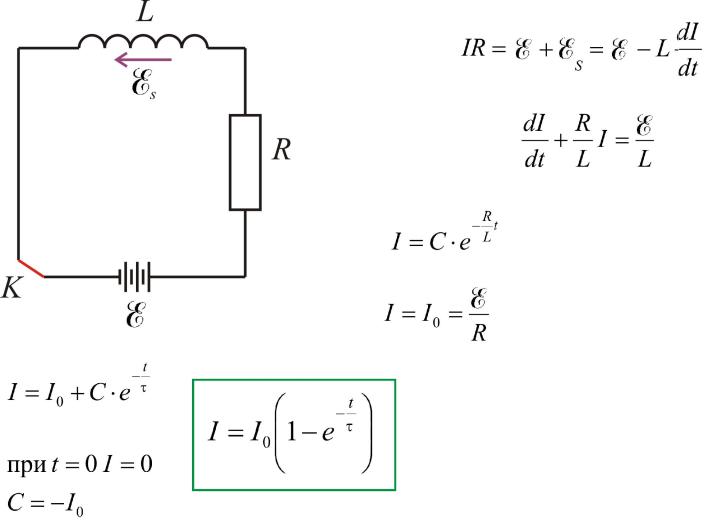
2.Замыкание цепи:
- общее решение однородного уравнения.
- частное решение неоднородного уравнения.
Данные выражения получены для случая, когда индуктивность L постоянна. Если индуктивность катушки зависит от силы тока (ферромагнитный сердечник), то в этом случае за счет слагаемого IdL/dt э.д.с. самоиндукции может достигать очень больших значений.
Энергия магнитного поля.
Крахалев М.Н.
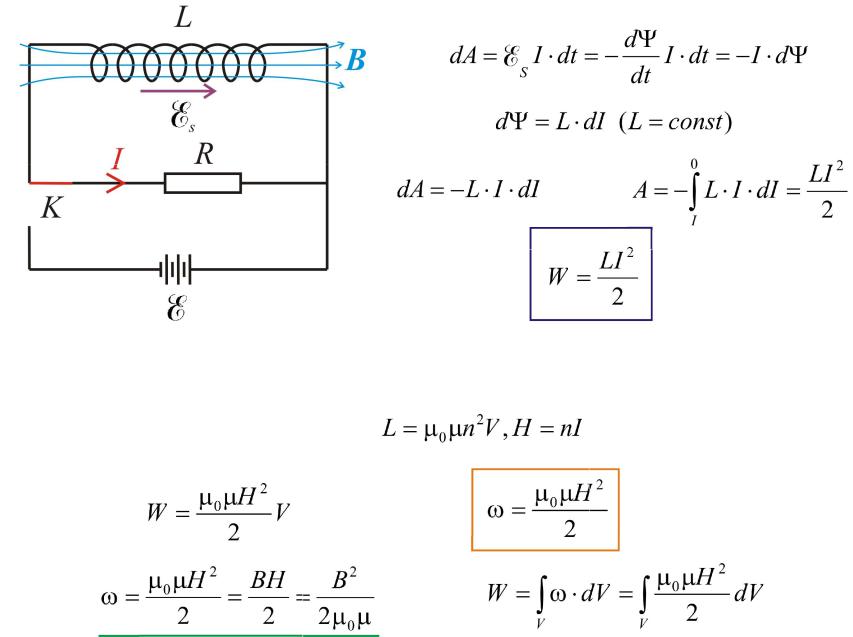
Проводник с индуктивностью L, по которому течет ток I, обладает энергией, которая локализована в возбуждаемом током магнитном поле.
Для бесконечного соленоида:
- плотность энергии магнитного поля.
