
- •Кафедра физики
- •Кафедра физики
- •Кафедра физики
- •Кафедра физики
- •РАБОТА ПО ПЕРЕМЕЩЕНИЮ ПРОВОДНИКА С ТОКОМКафедра физикиВ
- •Кафедра физики
- •Кафедра физики
- •Кафедра физики
- •Кафедра физики
- •Кафедра физики
- •Кафедра физики
- •Кафедра физики
- •Кафедра физики
- •Кафедра физики
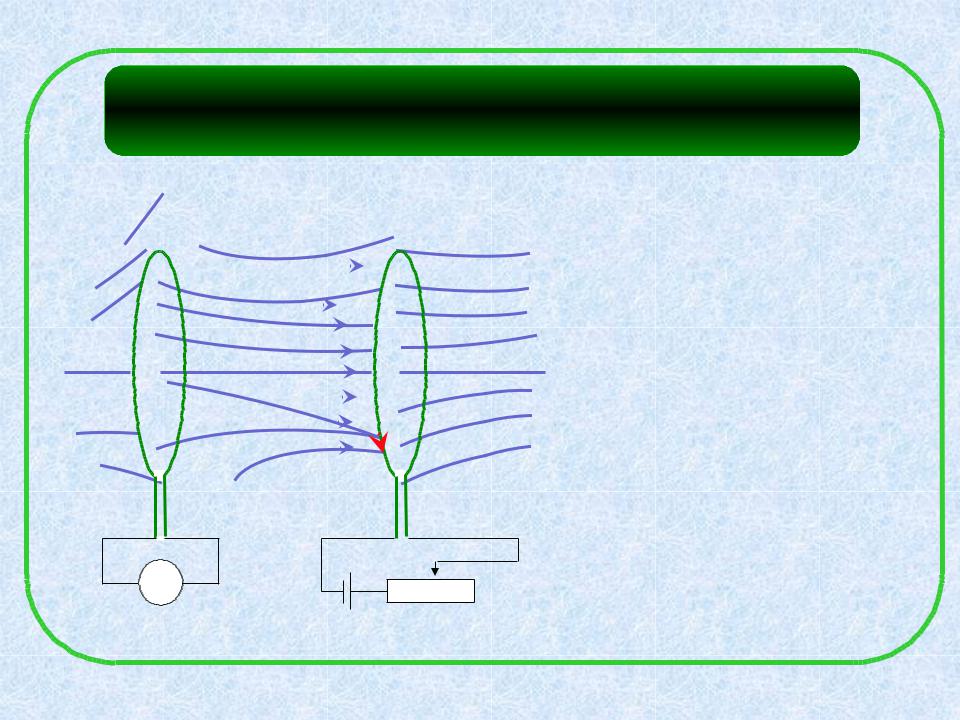
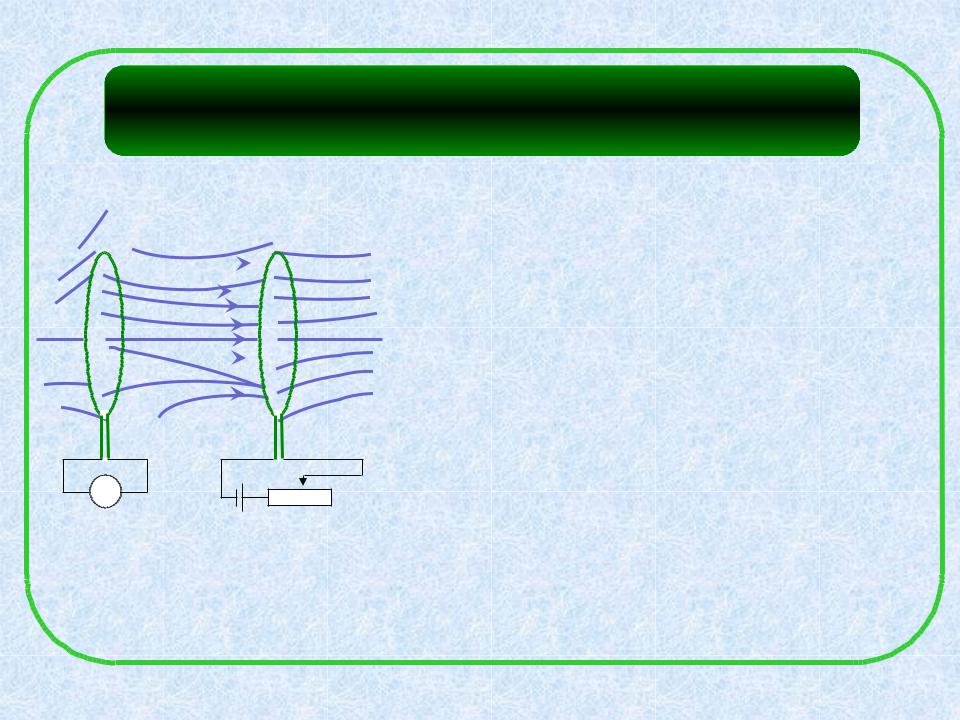
- •Посмотрим эксперимент.
- •Алюминиевое кольцо выталкивается и зависает над сердечником соленоида, подключенного к генератору переменного электрического
- •Кафедра физики
- •Кафедра физики
- •ЛОКАЛЬНАЯ ИЛИ ДИФФЕРЕНЦИАЛЬНАЯ ФОРМА ЗАКОНА ФАРАДЕЯ
- •Лекция №12 п.1 Проекция ротора поля
- •Лекция окончена

Кафедра физики
ЛЕКЦИЯ 7.2
ПЛАН ЛЕКЦИИ
1.Работа по перемещению проводника с током в магнитном поле.
2.Явление электромагнитной индукции.
3.Электродвижущая сила индукции.

Кафедра физики
РАБОТА ПО ПЕРЕМЕЩЕНИЮ ПРОВОДНИКА С ТОКОМ В МАГНИТНОМ ПОЛЕ
Если проводник с током перемещается в магнитном поле, то сила Ампера, действующая со стороны магнитного поля на проводник, совершает работу. Определим величину этой работы.
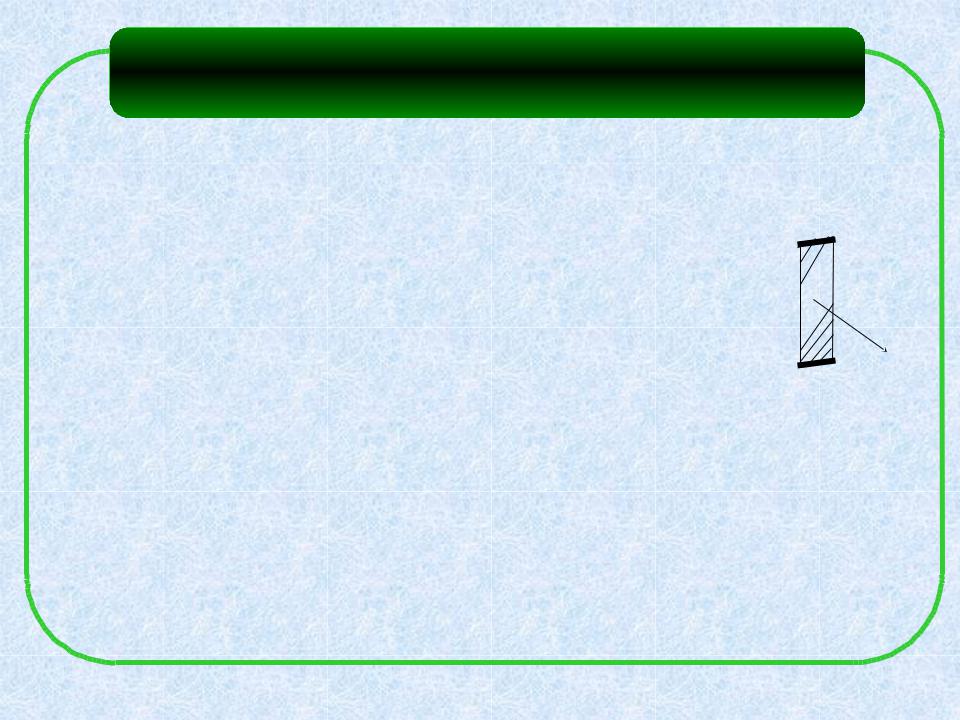
Пусть элемент тока |
Idl проводящего контура перемещается в |
магнитном поле с индукцией B на небольшое расстояние dr . |
|
Действующая на |
элемент тока сила Ампера F I dl ,B |
совершает работу |
dA F ,dr |
|
|
Подставим в эту формулу выражение для силы Ампера, получим:
dA I dr , dl ,B
Кафедра физики
РАБОТА ПО ПЕРЕМЕЩЕНИЮ ПРОВОДНИКА С ТОКОМ В МАГНИТНОМ ПОЛЕ
dA I dr , dl ,B
Получилась формула со смешанным произведением векторов. Такое произведение векторов обладает следующим свойством:
a, b,c a,b ,c |
Применим его и преобразуем |
формулу |
dA I dr , dl ,B I dr ,dl ,B
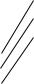 dr
dr
dS
dl
В получившемся выражении векторное произведение dr ,dl. можно трактовать как площадь dS , которую описывает элемент тока длиной dl при его перемещении на dr.

Кафедра физики
РАБОТА ПО ПЕРЕМЕЩЕНИЮ ПРОВОДНИКА С ТОКОМ В МАГНИТНОМ ПОЛЕ
dA I dr ,dl , B
В этом случае результат скалярного произведения будет выглядеть следующим образом: dA IBndS
BndS dФB - это магнитный поток через поверхность dS
В итоге получим: dA IdФB . Это выражение для работы,
которую совершает сила Ампера по перемещению в магнитном поле элемента тока.
Теперь определим работу по перемещению произвольного контура с током в постоянном однородном или неоднородном магнитном поле.
РАБОТА ПО ПЕРЕМЕЩЕНИЮ ПРОВОДНИКА С ТОКОМКафедра физикиВ
МАГНИТНОМ ПОЛЕ
Для этого необходимо разбить контур на элементы |
2 |
B |
|||
S |
|||||
тока, и суммировать работы по перемещению |
|
|
|||
каждого элемента тока. |
|
|
|
dr |
|
Проинтегрируем соотношение |
|
|
|||
|
dA IdФB |
|
1 |
S |
|
|
|
dS |
|||
для нахождения работы сил Ампера при |
|
|
dl |
||
перемещении |
контура |
из начального |
|
|
|
положения 1 в конечное 2: |
2 |
|
|
|
|
|
|
|
|
|
|
|
A IdФB IФB ФB |
||||
|
|
|
2 |
|
1 |
где ФB1 и |
|
1 |
|
|
|
ФB2 - значения магнитных потоков через поверхность, |
|||||
ограниченную контуром с током, до и после перемещения.
Работа, совершаемая силой Ампера при перемещении замкнутого контура с током в магнитном поле, равна произведению силы тока на изменение магнитного потока через поверхность, ограниченную контуром.

Кафедра физики
РАБОТА ПО ПЕРЕМЕЩЕНИЮ ПРОВОДНИКА С ТОКОМ В МАГНИТНОМ ПОЛЕ
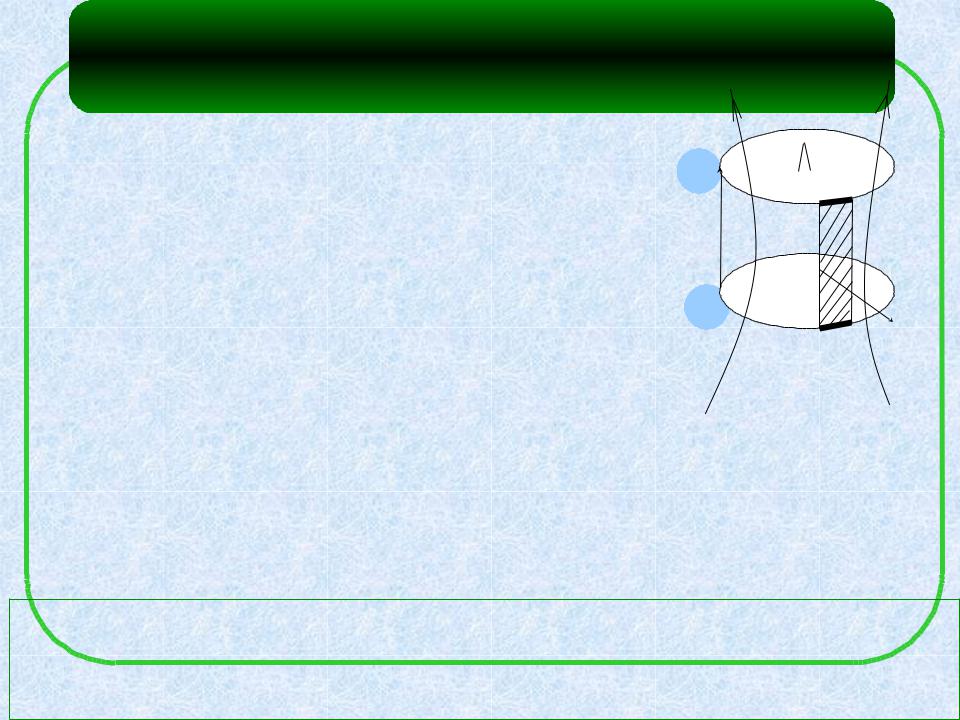
Пример. Плоский контур с током |
I поворачивают в магнитном |
||||
поле Bиз положения, при |
котором |
положительная нормаль |
к |
||
контуру направлена в сторону, противоположную полю ( |
n |
B |
|||
|
), |
||||
в положение, при котором |
n B |
|
|
|
|
Площадь, ограниченная контуром, равна |
S. |
|
|
||
Найти работу сил Ампера, считая, что ток |
поддерживается |
|
|||
постоянным. |
|
|
|
|
|
Кафедра физики
РАБОТА ПО ПЕРЕМЕЩЕНИЮ ПРОВОДНИКА С ТОКОМ В МАГНИТНОМ ПОЛЕ
|
|
1 |
|
I |
B |
I |
B |
n |
|
|
n |
2
A I Ф2 Ф1 , |
A I BS BS 2IBS |
Ф BS |
|
Ф21 BS |
A 2IBS |

Кафедра физики
ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ.
Электрические токи создают вокруг себя магнитные поля. Иначе, существует связь магнитного поля с током.
Эта фундаментальная задача была решена в 1831 году английским физиком Фарадеем, открывшим явление электромагнитной индукции.
Явление электромагнитной индукции состоит в том, что:
в замкнутом проводящем контуре при изменении магнитного потока, охватываемого этим контуром, возникает электрический ток.
Этот ток был назван индукционным
Появление индукционного тока означает, что при изменении магнитного потока в контуре возникает ЭДС индукции.
Кафедра физики
ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ.
2 |
1 |
Фарадей |
обнаружил, |
что |
||||
индукционный |
ток |
можно |
||||||
|
|
вызвать |
двумя |
различными |
||||
|
|
способами. Рассмотрим их. |
||||||
|
|
Фарадей проводил опыты |
||||||
|
|
с двумя контурами. |
|
|
||||
|
I1 |
В |
первом |
из |
них |
ток |
||
|
регулировался реостатом. |
|||||||
|
|
Во |
второй |
контур |
был |
|||
|
|
включен гальванометр |
|
|||||
|
|
Ток |
в |
первом |
контуре |
|||
G |
|
создает |
магнитное |
|
поле, |
|||
|
пронизывающее контур 2. |
|||||||
|
|
|||||||
http://www.physics.ru/courses/op25part2/design/index.htm
Кафедра физики
ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ.
2 1

 I1
I1
G
Способ 1. Контуры неподвижны. Если увеличивать ток I1 , поток магнитной индукции через контур 2 будет расти.
Это приведет к появлениюI в контуре 2 индукционного тока , который регистрируется гальванометром2 G
Уменьшение тока вызовет убывание магнитного потока через контур 2. В этом контуре появится индукционный ток противоположного направления.
